
«قبل وجود أيّ شيء، كانت الفوضى» هيسويد 2006.
مقدمة
جذبت أشكال الجبال، والسحب والأشجار، والنجوم وتدفق مياه الأنهار اهتمام البشر منذ أقدم العصور. كما اهتم العلماء بالبحث في الكون، وحركة الكواكب، وأمواج المحيطات، وبِنية وديناميكية الكون.
أدّى البحث وراء طبيعة الكون التي تبدو معقدةً وفوضويةً إلى ظهور نظرية الفوضى وعلوم الأنظمة المُعقدة، فنظرية الفوضى والبحث في علوم إدارة الكوارث ونظريات الأنظمة المعقدة ترتبط ارتباطًا وثيقًا بسلوك الأنظمة الديناميكية.فبعد تقديم النظرية الفيزيائية الشهيرة «أثر الفراشة» لإدوارد لورينتز تمّ طرح علوم نظرية الفوضى وحساباتها بشكل تدريجي وكان بينويت مانديلبورت أول من قدّم حساباتٍ لنظرية الفوضى عام 1975.
تعتبر مجموعة مانديلبورت من أكثر (الكسريات-fractals) تعقيدًا وهي تابعة لواحدة من أبسط القواعد الرياضية.
يتمّ إيجاد قواعد نظرية الفوضى في الحدّ المطلق لمعادلةٍ رياضية بسيطة، فبالنسبة لنظريّة مانديلبورت؛ أبسط القواعد تخلق أشكالًا معقدة.
إدراكنا للطبيعة
بحث الفنّانون والنّقاد عن الطبيعة كمصدرٍ لاعتقادهم فيما يختص بالمبادئ الرئيسية للجمال والذوق، فاعتقادهم أنّ الجمال الظاهر في الفنّ والعمارة ما هو إلا مجرد انعكاسٍ للجمال الموجود في الطبيعة وبالتالي يعتبر أقلّ قيمةً من الجمال الطبيعي.
ولذلك؛ هناك سؤالٌ يتبادر إلى أذهاننا وهو كيف ولماذا نعتبر الطبيعة جميلة؟ هل لأننا معتادون عليها أم أنّ السبب شيءٌ أعمق بكثير، بالأحرى مطبوعٌ وراثيًا بداخلنا!
لذلك يمكننا ملاحظة أنّ معظم الأشخاص يستمتعون برؤية صورٍ للخضرة (الأشجار والزهور) والسهول الواسعة، فالمخّ يمكنه فقط تمييز مقدارٍ محدّد من المعلومات المعروضة كمحفز بصري.
فالطريقة التي ندرك بها الطبيعة تبين لنا القدرة الاستثنائية للتركيب والتحليل التي يمتلكها الدماغ، فعلى سبيل المثال عندما نشاهد بستانًا أو غابةً بها أشجارٌ متشابهة؛ يمكننا ملاحظة أنّ كلًّا منها مختلفٌ عن الآخر في الشكل، لكنّ أدمغتنا ستترجم المشهد بشكلٍ أبسط: «هناك عددٌ من الأشجار المتشابهة دون التركيز في التفاصيل» وهذه صفةٌ مميّزة للطريقة التي تمّ تركيب أدمغتنا بها لتبسيط وفهم المعلومات المرئية المعروضة.
وبشكلٍ غريزي كما هو مرجح، فقد قام مهندسو الكاتدرائيات القوطية بتصميم أعمدة ودعامات مختلفة لكنها تحمل تشابهًا في مظهرها العام.
نظرية الفوضى
في الماضي، تجنّب العلماء البحث في الأنظمة المعقدة خلافًا لعلوم نيوتن التي رأت العالم كآلةٍ لها نظام عدالة محدّد ومنتظم، ويمكن التنبّؤ به، على العكس من نظرية الفوضى والتي تأخذ في الحسبان عدم الانتظام، وعدم اليقين والقدرة على التنبؤ، وتربط بين علوم نيوتن المبسطة وعشوائية الفيزياء الكمية، بالإضافة إلى ذلك فإنّ النظرية حققت الوحدة والانسجام بين النظام والفوضى.
نظرية الفوضى تساعدنا على فهم الأنماط في الطبيعة، وقد تمّ استخدامها لوضع نموذج للنظم البيولوجية، والتي تعد من أكثر الأنظمة التي لا يمكن التنبؤ بها (العشوائية-Chaos).
تظهر هذه الأنماط في كل مكان حولنا بما في ذلك أنماط السحب، وتدفق الدم عبر الأوعية، وفروع الأشجار، وعلم الفلك وغيرها.
تنص نظرية الفوضى على «أنه في ظلّ ظروفٍ معينة، يمكن النظر إلى الأنماط المنتظمة على أنها نشأت من عمليات مضطربة وعشوائية». ونظرية الفوضى لا تركز على الفوضى وعدم القدرة على التنبؤ الكامنة بنظام ما لكنها تؤكد على النظام الكامن في السلوك الموحّد للأنظمة المتماثلة.
لذلك فالعديد من العلماء يرون أنّ مصطلح «الفوضى» فقير ولا يعبر عن النظرية بشكل كافي، وذلك لأنها تعطي للقارئ الانطباع بالعشوائية، فمن وجهة نظرهم أن في الطبيعة يمكن للعمليات البسيطة تحويل الأنظمة للتعقيد دون أي عشوائية.
قام تشالز جينكز في كتابه «عمارة الكون الوثاب» عام 1998 بدراسة تأثير نظرية الفوضى في العمارة، حيث يرى أنّ أنظمة النسب الإنسانية استندت على هندسة الطبيعة نفسها، وذلك قبل اختراع الميكروسكوب عالي الدقة، وأكّد جينكز أن الكسريات في العمارة «التصميمات الحلزونية أو السداسية» قد تمّ اختراعها من قبل بروس جوف وفرانك لويد رايت قبل أن يكتشفها العلم.
«في عين البشرية، الكسريات وسيلة لرؤية اللانهائية» جيمس جليك 1988
ما هي (الكسريات-Fractals)؟
الكسريات هي أشكال هندسية أو أنماط تم صنعها من نفس الأجزاء، أي أنها تعكس نفس البِنية للشكل العام، بمعنى آخر إذا نظرنا لكل جزء من مكونات الشكل سنرى صورةً للشكل الكلي.
أفضل طريقة لتعريف الكسريات هي من خلال خصائصها، فهي حادّة وغير منتظمة في الشكل، وتحمل (التشابه الذاتي-self-similar) وذلك يعني أنّ كل جزء مطابق للكل لأنها تتشكل بالتكرار، بمعنى آخر أنّ هناك تغييرًا شكليًّا يحدث بشكل متكرر يعتمد على الحالة الأولية.
هناك خاصية أخرى وهي التعقيد، فيمكن أن يتم وصفها بخوارزمية بسيطة، وذلك يعني أيضا أنّ تركيب معظم العناصر الطبيعية التي ليس لها بنية محددة منتظم. ومصطلح الكسريات مشتق من الكلمة اللاتينية (كسري-fractus) والتي تعني «مكسور» أو «غير منتظم» أو «خشن».
الهندسة الكسرية
تمّ تقديم هذا المصطلح لأول مرة من خلال الرياضي بينويت مانديلبورت في سبعينيات القرن الماضي لشرح تعقيد الطبيعة، فأوضح على سبيل المثال أنّ السحب ليست كروية والجبال ليست مخروطية، أي أنّ الطبيعة لا تحتوي على أشكالٍ منتظمة (شكل 1).
يتطلب تمثيل تطوّر سلوك الأنظمة المعقدة -غير الخطية- شكلًا هندسيًّا رياضيًّا يحمل تشكيلًا هندسيًّا كسريًّا «الأجسام العشوائية أو الغير منتظمة في الفراغ تسمّى الكسريات».

من أشهر الأشكال الكسريّة «رقاقة الثلج لكوش» (شكل 2) والتي تبدأ بمثلث متساوي الأضلاع يتم تقسيم كل جهة لثلاثة أجزاء ونستبدل منتصف كل جهة بمثلث متساوي الأضلاع، ويتم تكرار هذه العملية عدة مرات، تسمّى هذه الكسرية بالتشابه الذاتي لأنّها تكرر نفس الجزء المتطابق للجزء الكلي للشكل.
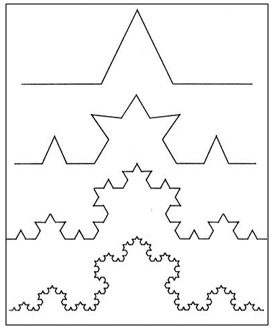
خصائص الهندسة الكسرية
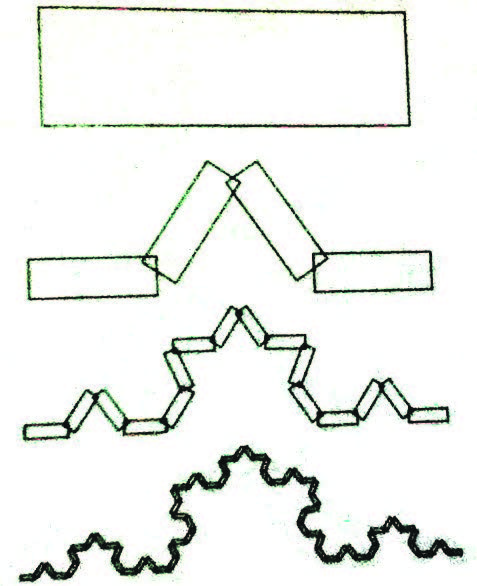
يكمن جوهر مفهوم الكسرية في أجزاء إضافية من التفاصيل تظهر عند عرض بنية الأشكال الكسرية عن قرب، كما تتميّز خصائص الهندسة الكسرية بالتشابه الذاتي، والتوسع أو التدرّج واللانهائية (شكل 3).
بالنسبة للتشابه الذاتي فتتميّز أجزاء بنية الكسريّات بالتشابه لذاتها أي أنّها تشبه الهيكل بأكمله، بغض النظر عن حجم الأجزاء الصغيرة، أمّا عملية التدرّج فهي تقليل و/أو تطور العناصر، أمّا اللانهائية فهي تُرى من الجانب النظري أكثر من الناحية العملية؛ ففي التركيبات الكسريّة يجب أن ينتهي التشعّب لحدٍّ معين، فحتى في الكسريات المولَّدة بالكمبيوتر يجب أن تنتهي عملية التوالد في مرحلة معينة وإلا تعطّل برنامج الكمبيوتر (شكل4).
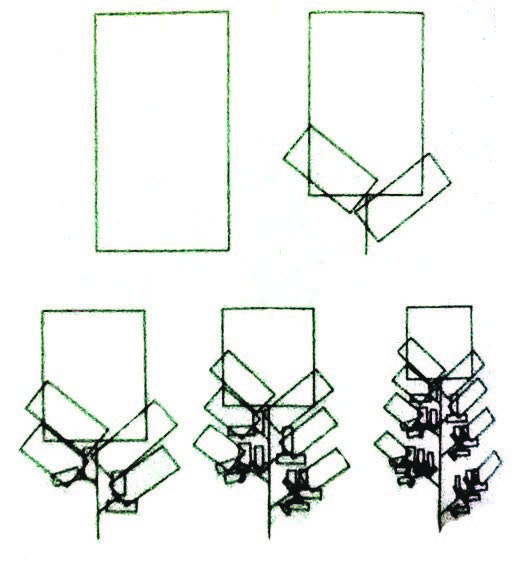
الهندسة الكسرية في العمارة
بالرّغم من أنّ معظم التشكيلات المعمارية تعتمد على هندسة إقليدس المَعنية بالأشكال التقليدية إلا أنّها تحمل بعض المكوّنات الكسرية، فقد تم تطبيق الهندسة الكسرية في العمارة بنطاق واسع لدراسة التشكيلات الكسرية للمدن، والمباني وأنماط التصميم.
يمكن أن يحدث التحليل الكسري في العمارة على مرحلتين:
- تحليل في النطاقات الصغيرة كتحليلِ مبنى (مكونات المبنى التي تتكرر بمقاييس مختلفة الحجم)
- تحليل في النطاقات الكبيرة كتحليل على المستوى العمراني (الكتلة العمرانية القياسية لتحديد القياس الكسري للمبني داخل المنطقة العمرانية)
تاريخ الهندسة الكسرية في العمارة
العمارة هي مرآةُ المجتمع وصورةٌ عامةٌ له، وتَبرز قيمة العمارة في وقتنا الحاليّ عن طريق ثقافة ما نبنيه، فالمعماريّ يترجم ويفسّر الأفكار الواعية والباطنة للمجتمع، وقد تناولت المجتمعات القديمة فكرة الهندسة الكسريّة في العمارة، يمكن تعقّب ذلك في مساكن المايا القديمة، حيث حلّل برون في بحثه أنّ الهياكل الكسريّة لمساكن المايا تظهر داخل المجتمعات وعبر المناطق بطرقٍ مختلفة: في المواقع والمستويات الإقليمية، وضمن المواقع الأثرية، بالإضافة لذلك فإنّ التنظيم المكاني في الأنماط الهندسية والترتيب أيضًا كسري، يتضح من خلال توزيع تكرارٍ حجمي علاقات المرتبة الحجمية داخل المواقع الجغرافية (شكل5).
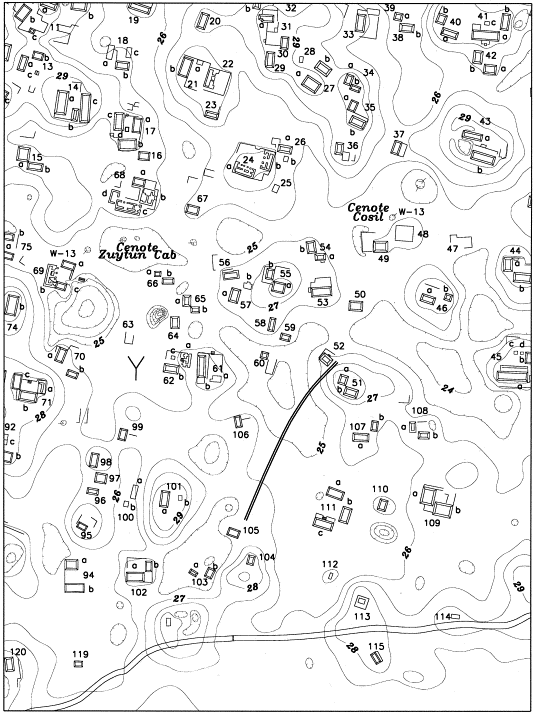
لذلك ترتبط الهندسة الكسرية في التكوين المعماري بالدراسة المنهجية لتطور التشكيلات المثيرة للاهتمام من أشكال الواجهات البعيدة للتفاصيل القريبة، وتحت هذا الفكر فهناك فتراتٌ محدّدة من التاريخ المعماري اشتهرت بالتشكيلات الكسرية مثل الطرز الكلاسيكية والآرت نوفو، حيث يمكن ملاحظة أنّ هذه المباني تميّزت بالتقسيمات الرياضية وبتدرّج التفاصيل التي تحمل التشابه الذاتي من أكبر المقاييس لأصغرها، ويقدم منزل فرانك لويد رايت (شكل6) مثالًا لتدرّج التفاصيل من الأكبر للأصغر، فغالبًا ما أشار رايت إلى الفكرة المركزيّة للتصميم على أنّ مصدرها الطبيعة.

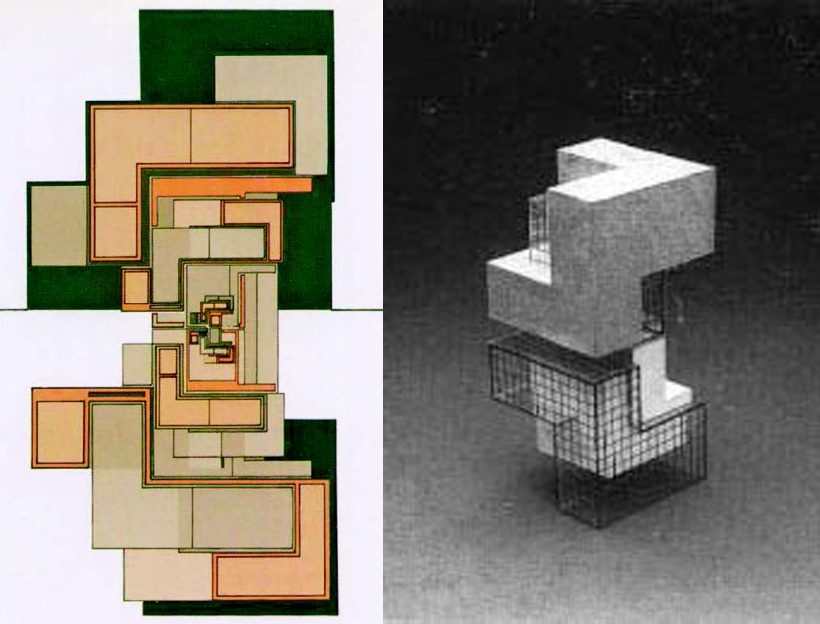
تمّ تقديم خصائص الكسريّات في العمارة في فترات الحداثة علي يد بيتر إيزنمان في عام 1978، ومن خلال منزل 11أ (شكل7) عرض إيزنمان مفهوم التدرّج الكسري.
تصميم منزل فينسيا (شكل 8) الذي قدّمه إيزنمان اتّبع ثلاثة مفاهيم تصميمية: الانقطاع والتكرار والتشابه الذاتي، فاستخدم حرف (L) المشتقّ من مربّعٍ تمّ تقسيمه لأربعة أجزاءٍ متساوية تمّ إزالة واحدٍ منها، وهذه الأجزاء تتجه للفراغ فلقد وصفها إيزنمان على أنّها غير مستقرة وبَينية، فالمقياس المنقوص الذي صمّمه ووضعه يمكنه أن يُنتج الشكل بمقاييس مختلفة الحجم، فمنزل 11أ على سبيل المثال يمكن إعادة تشكيله لتصميمات لانهائية، أي أنّه يحمل صفات التشابه الذاتي.

أمثلة الهندسة الكسرية في العمارة المعاصرة
مشروع ساحة اتحاد معامل العمارة بملبورن-Lab architectures’ project Federation square
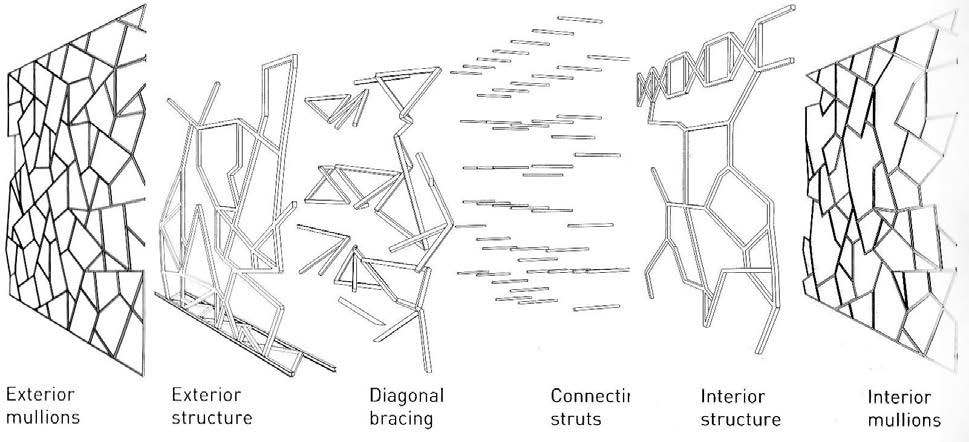
هذا المبنى المميّز بتشكيله المدني عن باقي المباني في الساحة تمّ تصميمه لتحقيق التعقيد وتأكيد قوة الشكل الهندسي (شكل 9)، فاختار المعماريّ الهندسة الكسريّة لإنشاء أنماط تصميميه من أجزاء بسيطة تسمح بالتكرار والاختلاف، تم تمثيل الواجهة الكسرية بواسطة نظام ثلاثي ذاتي التشابه متنامي.

تتكوّن وحدة البناء من الألواح الضخمة -خمسة تحديدًا- يتكون كلٌ منها من خمس بلاطات خرسانية، وتطلّ مجموعة المباني على الساحة لدمج الأنشطة الداخلية والخارجية.
صُمّمت واجهة المباني بمزيجٍ من ثلاثة مواد أساسيّة؛ الحجر والزنك والزجاج، وقد جعل التصميم المقياسي استخدام طريقة بناءٍ صناعية مسبقة الصنع أمرًا ضروريًا لعمليات الصيانة (شكل 10-11).
صُممت القاعة المفتوحة المزجّجة بنفس التكرارات (شكل12)، فالأنماط المتولّدة تكون إمّا بارزة أو غائرة لتحسين البنية المعقدة للمبنى.
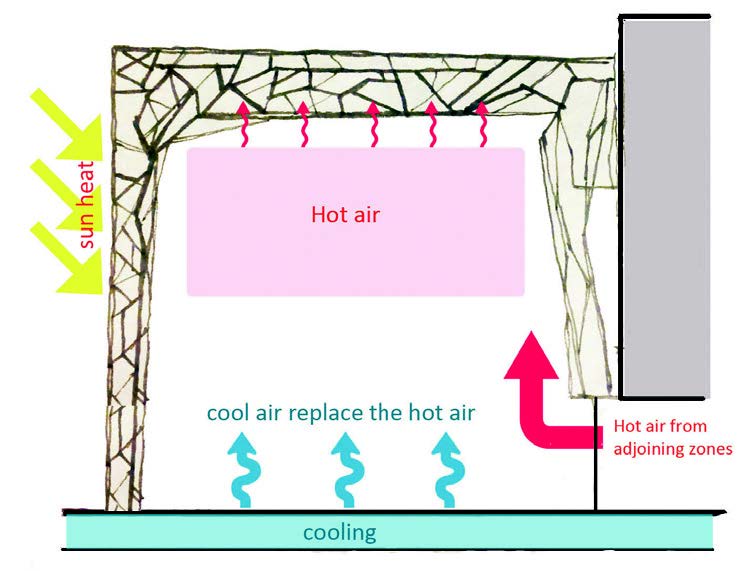
وقد تمّ تصميم الكسريات في المباني بصورة ثلاثية الأبعاد لتعمل كَحلّ بيئي للفراغات (شكل13).

المتحف المصري الكبير بمصر-The Grand Egyptian museum
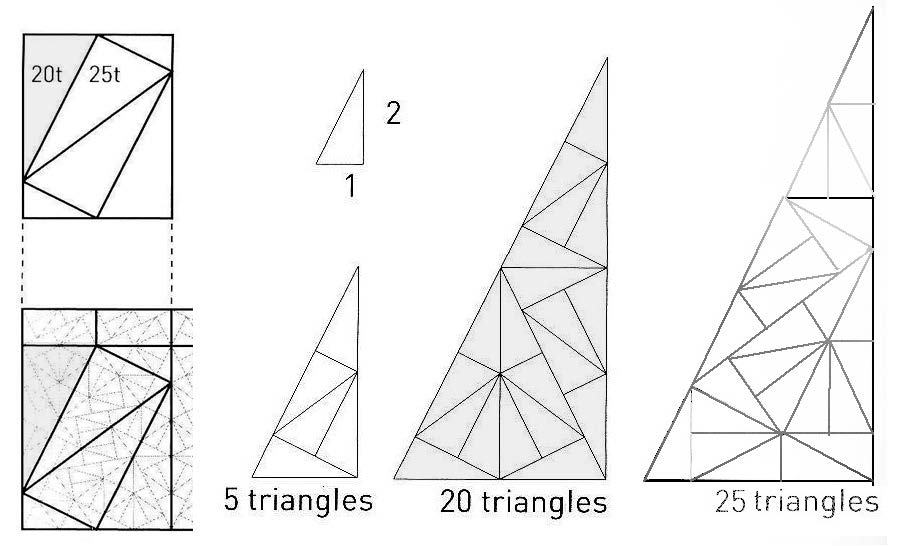
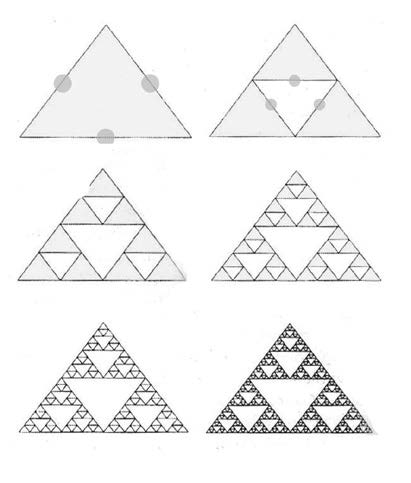
حمل المتحف المصريّ الكبير أفكارًا مشابهة لمباني ملبورن؛ فالتصميم الفائز لهينجان بينج تمّ تصميمه باستخدام أُطرٍ ضخمة تحيط بالمبنى تحمل كسريات مثلثة مستوحاة من (مثلث سيربينسكي-Sierpinski triangle)، تمّ استخدام تكرار العنصر علي واجهةٍ شفّافة مساحتها 750 متر طولًا و46 متر ارتفاعًا (شكل 14)، وقد تمّ إنشاء نظام سيربينسكي بواسطة واكلو سيربينسكي عام 1919.
يتم توليد الشكل الكسريّ عن طريق تكرار مثلث متساوي الأضلاع حيث ينقسم الشكل بواسطة عدد من التكرارات المتداخلة (شكل 15)

متحف فيكتوريا وألبرت بلندن-Victoria and Albert museum
البلاطات الكسريّة مصطلحٌ تمّ إطلاقه بواسطة المعماري دانيال ليبسكيند، حيث صمّم امتدادًا لولبيًّا لمتحف فيكتوريا وألبرت بلندن، واستخدم البلاطات كوحدات كسرية تجمع بين كونها عنصر يتم تكراره وجزء من عملية التبليط نفسها، تغطي هذه البلاطات طول الحائط اللولبي فتضيف للمبنى حركةً دائمة، تجعله يبدو غير مكتمل ويتطور باستمرار.

لمزيد من المعلومات برجاء الاطلاع علي الفيديوهات التالية:
http://https://www.youtube.com/watch?v=7_qwhmyGff8
https://www.ted.com/talks/ron_eglash_on_african_fractals/transcript?language=en#t-9973
https://youtu.be/IFA13ZC90e4?t=224
ترجمة وإعداد: ليلى جميل
مراجعة علمية: محمد رضا
تدقيق لغوي: هاجر زكريا
تحرير: سامح منصور
المصادر:
1- Osama A.,etal (PDF) FRACTAL GEOMETRY IN ARCHITECTURE: FROM FORMATIVE IDEA TO SUPERFICIAL SKIN DESIGN [Internet]. 2014 [cited 2018 Nov 29]. Available from: https://www.researchgate.net/publication/326033004_FRACTAL_GEOMETRY_IN_ARCHITECTURE_FROM_FORMATIVE_IDEA_TO_SUPERFICIAL_SKIN_DESIGN
2-Fathi M. THE ROLE OF FRACTAL GEOMETRY AND CHAOS PHENOMENON IN MODERN ARCHITECTURE. IJBPAS, December 4(12), Special Issue: 1493-1506 ISSN: 2277–4998 [Internet]. 2015 [cited 2018 Nov 20]. Available from: http://ijbpas.com/pdf/2015/December/1454497692MS%20IJBPAS%202015%20DEC%20SPCL%201156.pdf
3-Oakley D, Smith R. 2006 Building Technology Educators’ Symposium Proceedings. Lulu.com; 2008. 403 p.
4-Koç Ç, Sönmez M. THE ARCHITECT OF TODAY ON THE EDGE OF CHAOS; AN APPROACH THROUGH CHAOS THEORY. GAZI UNIVERSITY JOURNAL OF SCIENCE Part B: ART, HUMANITIES, DESIGN AND PLANNING [Internet]. 2017 [cited 2018 Nov 29];5(1):1-7–7. Available from: http://gujsb.gazi.edu.tr/article/view/5000211404

