إذا ذُكر مصطلح الشطرنج، ستجد ردور أفعال مختلفة من قِبل المحيطين بك، فتجد البعض قد أبدى إعجابه، وآخرين قد امتعضوا، وربما ستجد من سيتحمس لدرجة تجعله يطلب منك مبارزته في جولة ملحمية، ولذلك ستختلف انطباعات الكثير حول مدى استمتاعهم باللعبة. لكننا في هذه اللحظة بصدد الحديث عن لعبة لن يستطيع أحد مقاومة جاذبيتها وسحرها الخاص النابع من المبادئ الغامضة التي قامت عليها، إننا نتحدث عن شطرنج ولكن بإضافة سحر العلم لها خاصة «ميكانيكا الكم»، نحن بصدد الحديث عن الشطرنج الكميّة وكيف تختلف عن الشطرنج المألوفة لنا .
لذا رجاءًا لا تتذمروا من طول المقال، اقرأوا واستمتعوا بهذه القصة المثيرة.
يقص لنا مخترع ومصمم فكرة اللعبة نفسة كريس كانتويل- chris cantwell كيف بدأ العمل على ذلك النموذج من العاب الذكاء وجعله أكثر غرابة مما هو علية فيبدأ الحديث قائلًا: «منذ عامين وباعتباري طالب دراسات عليا في جامعة كاليفورنيا الجنوبية- USC فقد شرعت في العمل على لعبة ترتكز تقنيتها على علم ميكانيكا الكم وعندما أنتجت نسخة قابلة للعب منها؛ رشحني مشرفي العلمي تود برون- Todd Brun لأكون على اتصال مع سبيروس- Spiros Michalakis الباحث في مركز الفيزياء الوطني لدراسة المعلومات والمواد الكَمية “IQIM” والذي يعمل مع شركة جوجل في تصميم العاب مبنية على مبادئ الكوانتم مثل Qcraft والتي قُدّمت رسميًا من شركة Minacraft المعنية بألعاب العالم المفتوح والتي شرعت بإدخال مبادئ ميكانيكا الكم في العابها.»
يستطرد كريس قائلًا: «كان علي أن أثبت لسبيروس قدرة نموذجي الذي سأساهم به في تلك الألعاب، واعتدنا على تبادل أفكارنا الأولى كالعصف الذهني بيننا، في اجتماعنا الأول من كل أسبوع في كافيتريا chandler في جامعة كالتك، وبعد مِضي أكثر من عام، بدأنا نرى أن لعبة الشطرنج قد أخذت تتطور لصوره متقدمة، حتى أصبحت بصورة الشطرنج الكمية، وبدأنا نناقش فكرة عرض شريط فيديو يحتوي على عرض للعبة نقدمه أثناء الاحتفال بالإرث الذي ساهم به فاينمان أحد علماء الفيزياء النظرية الذي طور مجال الميكانيكا الكهروديناميكية في مجال ميكانيكا الكم في الحدث القادم في كالتك. وستشهد الأشهر القليلة المقبلة زوبعة بعد عرض هذا الفيديو، الذي سيتحول من مجرد معركة في الشطرنج الكمية إلى طفرة فى مستقبل البشرية.»
سنرى في هذا الفيديو مباراةً تدور بين الفيزيائي ستيفن هوكينج وبطل فيلم Ant-Man بول رود- poul Rudd من إخراج Alex winter هذه المباراة الملحمية تُدعى “أي شخص يستطيع ممارسة لعبة الكم” والذي عُرض لأول مرة في كالتك مساء يوم 26-1-2016 وانتشر سريعًا على الإنترنت كما لو كان فيروسًا. (يمكنك مشاهدة الفيديو من هنا)
إذا لم تكن قد شاهدته من قبل؛ فهذه اللحظة هي فرصة جيده لفعل ذلك.
دعونا نستعرض بعض الأسئلة عن ماهية تلك اللعبة؟ وما الذي نعنيه تحديدًا بالشطرنج الكَمية؟ وكيف تم بنائها على أساس فيزياء الكم؟
سنجد أن فيزياء الكم قد منحت كل قطعة من قطع الشطرنج، قوة مبدأ كمي من مبادئ ميكانيكا الكم، وقد اتخذت هذا المظهر الحديث مقارنة باستراتيجيات قطع الشطرنج المألوفة منذ مئات القرون، لذلك لن تحتاج أي معرفة بمبادئ الكم لممارسة اللعبة، ولكن بأخد الإعتبار بأن المعرفة بأساسيات الشطرنج المألوفة وفهمك لقواعدها واستراتيجياتها سيساعدك في البدء بممارسة اللعبة. ومع مرور الوقت؛ ستجد عقلك تدريجيًا قد اعتاد على بعض السلوك الغريب لحركات كل قطعة وفقًا لمبادئ الكم مثل (التراكب الكمي، التشابك الكمي، التداخل …إلخ).
تلك المعارك التي ستخوضها ستجعلك لاعبًا منظمًا، ستقدر على تحقيق مكسب فيها بنفس سهولة تحقيقه في لعبة XO.
من هنا؛ سيبدأ المقال بمناقشة مفهوم التراكب الكمي حتى تدرك آلية اللعب بسهولة، وما الدول الذي يلعبه في الشطرنج الكَمية مع الأخذ في الاعتبار وجوب مناقشة بعض المبادئ الكمية الأخرى مثل التشابك الكمي والتداخل وتأثير الرصد البشري على الجسيم ولكن في مقالات أخرى.
التراكب الكمي- superposition
بالنظر إلى الإلكترون بخصائصه الموجية، وبالإضافة لمعرفتنا بأحد خواص الموجات وهو التداخل البنّاء الذي يحدث عندما تكون قمتان أو قاعان لموجتان متراكبتين معًا؛ فنجد وفقًا لفزياء الكم أن الإلكترون يوجد في أكثر من موضع في نفس الوقت، وبعيدًا عن التفسير الفيزيائي المعقد؛ تسمى تلك الحالة بالتراكب الكمي، ولكن عند رصد الإلكترون فإنة يتخد موضعًا واحدًا فقط وهو الموضع الذي تم رصده فيه.
التشابك الكمي- entanglement
خاصية تتحكم في سلوك الجسيمات تحت الذرية، فإذا كان لدينا إلكترونان يفصل بينهما مسافة بأي قدر، فعند رصد أحدهما في موضع وتحديد اتجاه دورانه؛ فإننا نستطيع بكل سهولة استنتاج اتجاه دوران الإلكترون الآخر بأنه في الاتجاه المضاد للسابق.
إليك الآن نمط القواعد الذي يجب أن تسير عليها في الشطرنج الكمية
1- اللاعب لديه المقدرة على تنفيده نقلات مكمّاه (أي لها خاصية مما تم ذكره سابقًا) هذا بالإضافة إلى قدرته على تنفيذ نقلات الشطرنج المألوفة.
2- لدى اللاعب في كل دور حرية اختيار نوع حركة القطعة، سواء كانت نقلة مألوفة أو نقلة كَمية، بالرغم من أن النقلة الكَمية تخلق حالةً من التراكب الكمي على لوحة الشطرنج.
(إذا كنت قد رأيت فيلم ستار تريك؛ المقطع المتعلق بلعب الشطرنج ثلاثية الأبعاد 3D فيمكنك بسهوله تخيل الأمر السابق بطريقة مماثلة).
3- من الممكن لكل قطعة أن تتواجد في أكثر من مربع على لوحة الشطرنج وفقًا للتراكب، ومع ذلك فإنّ عدد احتمالات تواجد أي قطعة على مربع من المربعات غير ثابت وفقًا لقوانين الشطرنج الكّمية، وهو قابل للزيادة أو النقصان بمعنى أدق: (جميع احتمالات تواجد القطعة على اللوحة هي احتمالات حالة التراكب الكمي لا تستطيع تحديدها إلا بعد حركة الخصم) سيتم توضيحها أكثر تاليًا.
4- يُقَدّمْ في دور اللاعب فرصة واحده له لإعطاء قطعته خاصية التراكب الكمي.
5- أي نقلة سوف تؤثر على باقي القطع الموجوده في نفس الوقت.
6- في كل مره يقوم اللاعب بنقله كمية؛ فإن عدد احتمالات القطع الموجوده في حالة تراكب ستتضاعف.
دعنا نلقي نظرة على بعض الصور التي قد تزيد رؤيتنا وضوحًا:
تبدأ اللعبة بنفس الترتيب الموجود في الشطرنج المألوفة، وكل بيدق (جندي) سواء أبيض أو أسود؛ سوف يتحرك بنفس النقلات المألوفة، بينما تمتاز باقي القطع للمتنافسين بقدرتها على اختيار نوع حركتها إما حركه كَمية أو حركه مألوفة.
لتوضيح أكثر: النقله المألوفة تأخد نفس النمط الموجود في الشطرنج المألوفة، بينما النقله الكمية تخلق نوعًا من التراكب الكمي عند نقلها.
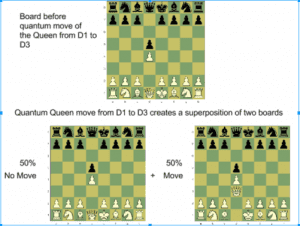
وسنرى الآن مثالًا لحركة كَميّة للوزير الأبيض
في المخطط السابق وعند حدوث اختيارنا للقيام بحركة كميّة للوزير الأبيض للإنتقال من d1 إلى d3 فإنه سيصبح متواجد في حالتين على اللوحة؛ فستجد في إحدى اللوحتين أنه لم ينتقل إلى d3 وفي اللوحة الأخرى قد انتقل، ونسبة حدوث كل منهما هي (%50 : %50)، ولكي يتم عرض جميع احتمالات تواجد الوزير على اللوحة -الأمر الذي سوف يجعله معقدًا للاعب، إذا ما قام بعدة نقلات كَميّة أخرى- ولكي نتحاشى هذا التشويش؛ فإن اللاعب سوف يرى أي نقلة للقطع المكمّاه بتواجدها في موضعين على نفس اللوحة، لذلك؛ إذا تم نقل الوزير بحركه كَمية؛ فسيرى الخصم هذا المشهد أمامه.
ملاحظة أخرى وهي أن الجزء الغير ملون فوق قطعة الوزير يوضح احتمالية التراكب الكمي (تواجد الوزير في موضعين فى نفس الوقت)، لكن خلال النقلة المقبلة لصاحب الفريق الأبيض؛ يجب عليه أن يختار حالة الوزير على اللوحة وكيف سينتقل إلى مربع آخر وفقًا للحالة التي سيختارها له.
دعنا نستعيد الحديث عن حركات الوزير، ربما تتسائل متعجبًا: ماذا سيحدث لو أردت تحريك قطعة وهي في حالة تراكب كمي؟
الإجابة هي أن الوزير بينما يكون متواجدًا في موضعين معًا، ستتاح فرصة الاختيار لاحقاً إما بنقل الوزير أو إبقاءه في موضعه الأصلي، أي أن لك الحرية في تنفيد خطوات كمية أو مألوفة على تلك القطعة حينها.
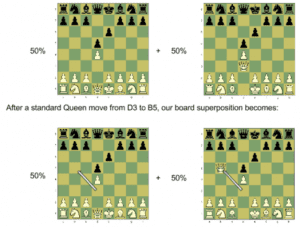
دعنا نرى محاولتنا لتنفيذ نقلة مألوفة للوزير الموجود في حالة تراكب كمي بدلًا من نقلهِ نقلةً كمية، وستجد أن النتيجة كما في الصورة التالية.
بعد نقل الوزير نقلة مألوفه من d3 إلى b5 فإن التراكب الكمي يحدث على الصوره التالية لحالتي الوزير، سيتأثر كل مربع على اللوحة بحالة تراكب كمي نتيجة تلك النقلة، فتجد أن فرصة انتقال الوزير من d3 إلى b5 تتساوى مع فرصة بقاءه في موضعه الأصلي وعدم انتقاله إلى أي مربع بنسبة (%50 : %50)
وسيرى اللاعب كما هو موضح فى الأسفل حدوث تراكب كمّي لموضع الوزير الجديد في المربع b5 مرة أخرى بنسبة (%50 : %50)، وسوف تجد أن ما حدث هو مجرد مثال على انتقال قطعة مكمّاه بواسطه نقلة مألوفة، بينما النقله الكَمية ستعمل مثلما ذكرنا من قبل.
ربما لاحظ البعض أن أي نقلة كَمية تعني لك فرصة تلاشي دورك التالي بتثبيت قطعتك كما هي، أي أن تمررها لخصمك ولكن المفاجأة أن هذا ليس من الأمور المثيرة التى يرجح فعلها معظم اللاعبين، لهذا السبب تم إضافة النقلات الكمية لكي تزيد من خيارات قطع الشطرنج، حيث أنه بواسطة النقلة الكمية تستطيع اختيار مربع هدف على اللوحة لتصل إلية سريعًا، مقارنةً بقدرتك على الوصول إلية بنقلتين من الشطرنج المألوفة.
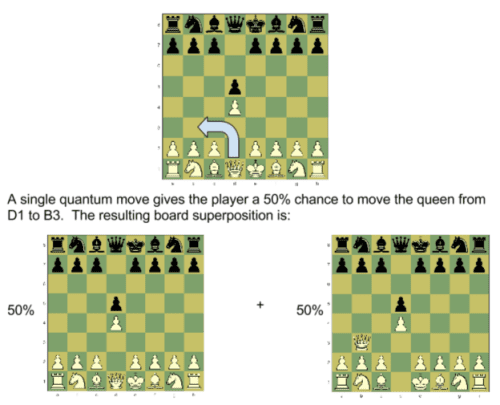
فعلى سبيل المثال؛ ووفقًا للشطرنج المألوفة، فإنك تستطيع اختيار هدف محدد للوزير لنقلة خطوتين إلى الأمام ثم خطوتين إلى اليسار مع مراعاة أن هذا يتطلب دورين متتاليين كالتالي:
نقل الوزير من d1 إلى d3 في الدور الأول، ثم نقلة من d3 إلى b3 (انظر في الصوره التالية للتوضيح)
بينما نجد وِفقًا للشطرنج الكَمية؛ أن النقلة الكمية تجعلنا قادرين على نقل الوزير من d1 الى b3 في دور واحد فقط بفرصة قدرها %50.
ستجد بعد النظر إلى الصورة السابقة للنقلة الكمية للوزير، حصولنا على احتمالية (%50) للانتقال إلى b3 إن تحقق، واحتمال (%50) أن لا شيء قد يحدث وسيظل الوزير في موضعه الأصلي، وإذا وضعت نفسك مكان اللاعب؛ فعليك أن ترى لوحة الشطرنج، كما هى موضحة بالأسفل، هناك فرصة قدرها (%50) أن يكمل الوزير ما يعادل نقطتين مألوفتين فى دور واحد (إذا تحرك حركة كمية)
لا تقلق فالأمر لا يسير بعشوائية كما تظن.
الحقيقة أن التراكب الكمي الذي يصيب القطع على مربعات لوحة الشطرنج يجعل من حركتها (حركة أُحادية) وهي كلمة مجازية لوصف كيف تسير الأمور بشكل كَميّ والتي بدورها تؤدي إلى أحداث مثيرة للانتباه.
الآن سوف أختم هذا المقال آملًا أن أكون قد أوضحت بعض الأفكار عن كيف يؤثر مبدأ التراكب الكمي في الشطرنج الكَميّة.
وسوف أعرض مبدأ التشابك الكمي في المقال القادم وربما سأذهب لما هو أبعد من ذلك بشرح التحريك الكمي.
إعداد: Muhammad Deshesh
مراجعة: Matalgah Hamzeh
المصدر: http://goo.gl/pSLUHr
#الباحثون_المصريون