
«دوائر فورد – Ford Circles» وعودة العلاقات القديمة بين الجبر والهندسة!
1- هاجس هيلبرت.
2- الرياضيات عند القدماء.
3- الملامح الأولى للانفصال.
4- أمنياتنا القديمة تتحقق.
5- جمع فيري.
6- الكسور غير القابلة للاختزال.
7- عينة من الكسور غير القابلة للاختزال في الفترة من 0 إلى 1.
8- دوائر فورد.
«هاجس هيلبرت»:
“هل ستلقى الرياضيات مصير العلوم الأخرى التي انتهى بها المطاف منقسمة إلى أفرع مستقلة من العلوم؟ أنا لا أعلم إذا كان هذا سيحدث فعلا ولكن أتمنى ألا يحدث. العلوم الرياضية في رأيي هي كل لا يتجزأ ومع اتساع المعرفة الرياضية يصبح ذلك خطرا يهدد الوحدة العضوية للعلم. إن الوحدة العضوية للرياضيات هي ملازمة لطبيعة هذا العلم، حيث أنها حجر الأساس لكل أنواع المعرفة المتعلقة بالظواهر الطبيعية”.
عملية فصل العلوم الرياضية عن بعضها كانت هاجسا يراود «ديفيد هليبرت – David Hilbert» عالم الرياضيات الشهير الذي دائما ما أصر على أنه في ظل هذا الزخم التطوري للعلوم الرياضية ستفضي بها مستقلة منفصلة لا أواصر بينها.
«الرياضيات عند القدماء»:
لأولئك القدماء الذين لم يخوضوا في عمليات الترميز المتتابعة لأرقام حسابية على وجه التحديد أو جبرية بصفة عامة. كان علم الحساب مغلفا في إطار هندسي خالص، فمثلا كانت تستخدم مساحة المستطيل للتعبير عن عملية رياضية أساسية مثل حاصل ضرب عددين والذي تكون أضلاعه عبارة عن قيمة هذين العددين في عملية الضرب.
«الملامح الأولى للانفصال»:
ولم ينفصل الجبر و علم الحساب عن الهندسة الرياضية إلا مؤخرا بعد التطور المذهل في العلوم الرياضية. وكانت أولى ملامح هذا الانفصال عن طريق التقديم المنهجي «للتأشير الجبري – Algebraic Notations» في القرن السادس عشر. ويسمى لغة الجبر، وهو باختصار جميع الرموز الجبرية التي يمكنك أن تتخيلها والتي تعبر عن الأرقام الجبرية كمتغيرات في صيغ ومعادلات رياضية: x ، y ،z ، ≪ ، ∛φ , ∄ ،≅ ، +، -،π وغيرها من الرموز. وفي القرن السابع عشر ابتكر الفيلسوف والرياضي «رينيه ديكارت – Rene Descartes» ،والذي يلقب بأبي الفلسفة الحديثة، نظام الإحداثيات الديكارتية التي شكلت النواة الأولى لفرع من علم الرياضيات يسمى «الهندسة التحليلية – Analytic Geometry» مدعيا أن أي مسألة هندسية يمكن حلها جبريا. والذي يعتبر ساريا من حيث المبادئ فقط وذلك لأن تقليص المسائل الهندسية غالبا ما سيقودنا إلى معادلات جبرية أثناء إيجاد طريقة لحلها. والتي تعتبر طرقا تقريبية للحلول الهندسية، ومازالت الرياضيات تعمل بطريقتها الخاصة. وفي أيامنا هذه يعتبر الجبر والهندسة علمين منفصلين تماما، ولكن الروابط القديمة بينهما يبدوا أنها بدأت في الظهور من جديد والتي هي مفاجئة في مقدار بساطتها متمثلة في دوائر فورد.
« أمنياتنا القديمة تتحقق!»:
بعفوية شديدة عند بداية دراستنا للكسور الاعتيادية في المراحل التعليمية الأولى، كنا نظن أن ناتج عملية جمع الكسور الاعتيادية عملية مباشرة تتضمن عملية جمع البسط مع البسط والمقام مع المقام.
من كان يتخيل أنه سيأتي اليوم الذي سنكتشف فيه أن الأخطاء التي كنا نرتكبها في عمليات جمع الكسور الاعتيادية والتي طالما وبخنا عليها مدرسوا الرياضيات فتحت الباب من جديد لربط مفاهيم الهندسة الرياضية بعلم الجبر.
نتذكر جميعا الكسور الاعتيادية والعمليات المزعجة عليها والتي كنا نتمنى أن تكون أكثر بساطة. فعملية الجمع للكسور A/B و C/D، والتي يجب أن نوجد قاسما مشتركا أكبر لكلا الكسرين تكون كالآتي:
A/B + C/D = A.D+C.B / B.D.
«جمع فيري – Farey Addition»:
ولكن ماذا لو تحققت أمنياتنا القديمة الآن وقمنا بعملية الجمع لكل من البسط والمقام بصورة مباشرة؟
A/B + C/D = A+C / B+D.
يا للروعة لا يوجد أسهل من ذلك! ستبتهج بسهولة المسألة وتمضي قدما إلى شيء آخر هذا غالبا ما سيفعله معظم الناس، ولكن الرياضيين سيتصرفون بطريقة مغايرة تماما.
فعندما يجد الرياضيون نمطا ملفتا للانتباه يبدءون التساؤل هل ما يحدث مجرد صدفة أم أن هنالك حقيقية عميقة تختبئ خلف هذا النمط؟
وبالفعل وجد الرياضيون نمطا مثيرا تتخذه نوعية معينة من الكسور تسمى الكسور «الغير قابلة للاختزال – Irreducible Fraction» عند جمعها بهذه الطريقة المباشرة وسميت عملية الجمع هذه باسم «جمع فيري – Farey Addition» أو «الجمع الوسيط – Medians Sum».
«الكسور الغير قابلة للاختزال – Irreducible Fraction»:
الكسر A/B يقال أنه غير قابل للاختزال إذا كانت الأعداد A وB أعدادا صحيحة وكانت أولية فيما بينها Coprime Numbers أي أن القاسم المشترك الأكبر بينهما هو الواحد الصحيح (أي أن البسط والمقام يشتركان وفقط في كون العدد واحد هو أكبر قاسم مشترك لكل منها).
على سبيل المثال: 14 و 15 هما عددان أوليان فيما بينهما حيث إذا قمت بتحليل أي منها إلى عوامله الأولية (3*5=15 , 2*7 =14)، لا يوجد بينهم قواسم أولية مشتركة أكبر من الواحد الصحيح. بينما 14 و21 ليسا أوليان فيما بينهما
(3*7 =21 , 2*7 =14) حيث يتشاركان قاسما أوليا مشتركا وهو الـ7 .
مثل 2/5 و 6/7 و 29/12 هي كسور غير قابلة للاختزال، بينما 18/12 ليست كذلك حيث يمكن تقليصها (18/12 = 9/6 = 3/2).
«في الفترة المغلقة من الصفر إلى الواحد»:
حسنا رجوعا إلى عملية «جمع فاري – Farey Addition» وإذا أردنا حصر جميع الكسور الغير قابلة للاختزال في الفترة المغلقة من الصفر إلى الواحد حيث أن الواحد والصفر هما كسور أيضا سيكون لدينا عدد كبير جدا من الكسور تصل إلى عشرات الآلاف ولذلك سنختار عينة منها حيث يكون المقام عددا محددا أي رقم وليكن أقل من 250 .. لا يوجد شيء مميز في هذا الرقم هو رقم مختار عشوائيا لتقليل العدد الكبير جدا من الكسور والتي يمكن أن تحصل عليها في الفترة المغلقة من الواحد إلى الصفر، وباستخدام برنامج حسابي وباختيار عينة عشوائية من هذه الكسور- كما هو مبين في الصورة- يتضح النمط الذي تسلكه هذه الكسور جميعا، حيث يمكن تمثيلها بعلاقة رياضية وهي جمع فيري، اختر أي كسر منها بطريقة عشوائية ستجد انه كسر وسيط بين الكسر الذي يسبقه والذي يليه. وكما هو موضح في الصورة الكسر المحدد بالخط الأحمر 48/73 هو الكسر الوسيط لكل من 119/181 و 121/184 (119/181 + 121/184 = 240/365 = 48/73).
وكذلك الكسر المحدد بالخط الأخضر 91/138 هو الكسر الوسيط لكل من 151/229 و 122/185 (151/229 + 122/185 = 273/414 = 91/138).
وهكذا يمكنك اختيار أي كسر منها بطريقة عشوائية وستجده منطبقا على جمع فيري.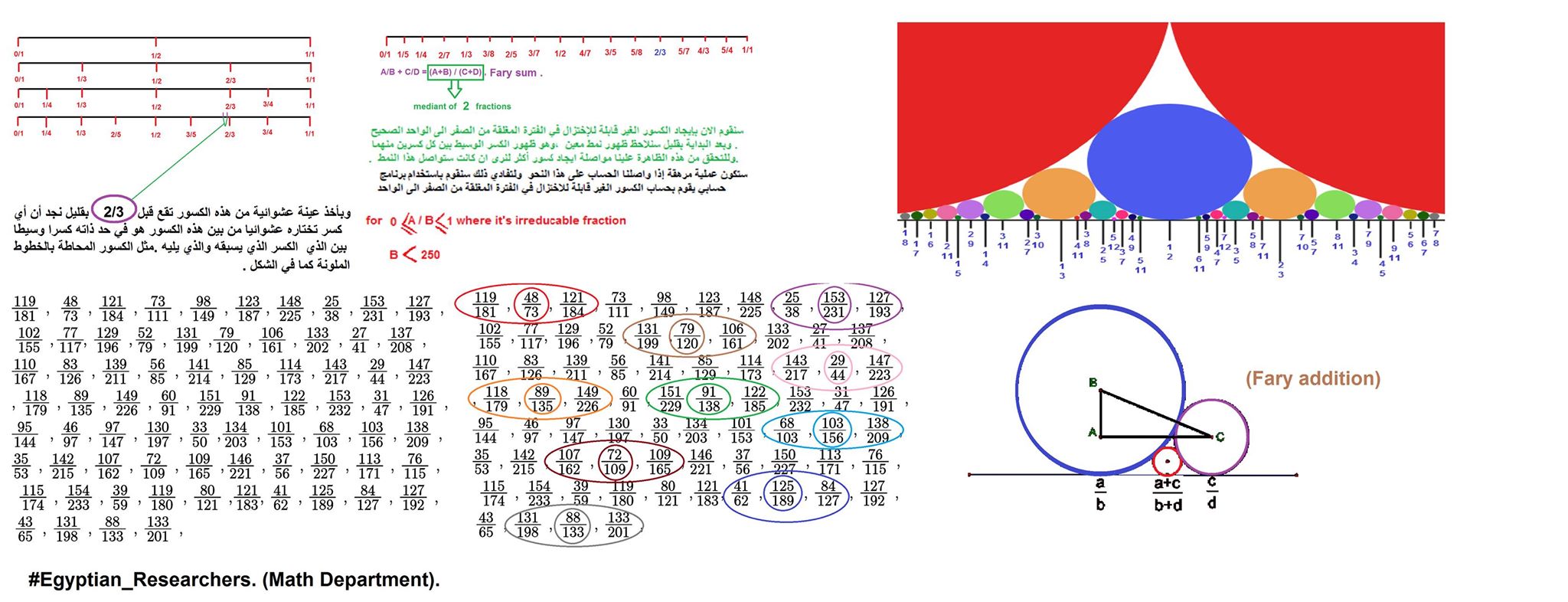
«دوائر فورد – Ford Circles »:
تعرف دائرة فورد على أنها الدائرة التي مركزها (a/b , 1/b2) و المماسة لخط الأعداد في النقطة a/b وقطرها مقلوب b2 (مقلوب مربع b) حيث أن a/b هو كسر غير قابل للاختزال إذا كل من a وb هي أعداد أولية فيما بينها Coprime Numbers.
وبتمثيل دائرة فورد لكل كسر غير قابل للاختزال سينتج لنا سلسلة لانهائية من الدوائر المماسة لبعضها والمماسة لخط الأعداد، ودوائر فورد هي حالة خاصة من التماس؛ حيث تكون الدوائر مماسة لبعضها ومماسة لخط الأعداد. لا يهم عدد الـa وb فمهما اخترت أعداد أكثر لن تتقاطع هذه الدوائر أبدا وكلها ستكون مماسة لخط الأعداد الممثل في المحور السيني، وهي مماسة لبعضها البعض بالتأكيد ولأي عدد نسبي هنالك دائما دائرة فورد يمكنها تمثيله.
إعداد:Ahmed Hosiny
نشر وتحرير:Mehmed Schaalan

