الحالات الطوبولوجية للمادة – جائزة نوبل في الفيزياء (2016)

على عكس التوقعات والتي كانت تصب في صالح تجربة LIGO التي اكتشفت موجات الجاذبية قبل عام (تم الإعلان عنها في فبراير 2016) إلا أن لجنة نوبل خرجت علينا اليوم وأعلنت أن الجائزة هذا العام ستذهب إلى فيزياء المادة المكثفة (Condensed Matter Physics) وبالتحديد إلى ثلاثة علماء قاموا بالدراسة النظرية لحالات المادة الطوبولوجية، هذا الموضوع غريب وربما لم يسمع به القارئ العربي العادي من قبل وسنحاول تبسيطه اليوم وبيان أهميته التي جعلته يستحق الجائزة الأشهر.

في البداية هذه ترجمة البيان الصحفي الذي أصدرته لجنة نوبل:

تُمنح نصف جائزة نوبل في الفيزياء 2016 إلى ديفيد ثاولز (David Thouless) من جامعة واشنطن، والنصف الثاني إلى فريدريك دانكن هالدين (Frederick Duncan Haldane) من جامعة برينستون وجون مايكل كوسترليتز (John M. Kosterlitz) من جامعة براون.

الفائزون هذه المرة فتحوا الباب لعالم مجهول تكون فيه المادة في حالات غريبة، فقد استخدموا أدوات رياضية متقدمة لدراسة حالات غير عادية للمادة كالموصلات الفائقة والموائع الفائقة والأغشية المغناطيسية. وبفضلهم يسعى العلماء في يومنا هذا إلى اكتشاف حالات أغرب من المادة، يأمل الكثير من الناس أن تكون لها تطبيقات مستقبلية في علوم المواد والإلكترونيات.

استخدام الفائزون لمبادئ الطوبولوجيا في اكتشافاتهم كان حاسمًا. فالطوبولوجي (Topology) هو فرع الرياضيات الذي يصف الخواص التي تتغير فقط بخطوات محددة، وباستخدامهم الطوبولوجي قاموا بإبهار الخبراء؛ ففي أوائل السبعينات أثبت مايكل كوسترليتز وديفد ثاولز أن التوصيلية الفائقة والميوعة الفائقة يُمكن أن تحدث في الطبقات الرقيقة، على عكس ما كان سائدا في ذلك الوقت. فقد بينوا أنها يُمكن أن تصبح موصلًا فائقًا، وأيضًا وضحوا الآلية التي تختفي بها خاصية التوصيل الفائق عند رفع درجة الحرارة.

وفي الثمانينيات قام ثاولز بتفسير تجربة سابقة تمت على طبقات رقيقة من مادة موصلة عُيِّن فيها التغير في التوصيلية الكهربية بخطوات من أعداد صحيحة، وبيّن ثاولز أن هذه الخطوات هي خطوات طوبولوجية. وفي الفترة نفسها كان دانكن هالدين قد اكتشف كيفية استخدام الطوبولوجي في دراسة خواص السلاسل المغناطيسية التي توجد في بعض المواد.

نحن الآن نعرف العديد من الحالات الطوبولوجية للمادة؛ ليس فقط في الطبقات الرقيقة، بل أيضًا في المواد العادية ثلاثية الأبعاد. وفي العقد السابق دفعت المواد الطوبولوجية البحث في فيزياء المادة المكثفة. وليس السبب أنها قد تُستخدم فقط في صنع جيل جديد من الإلكترونيات أو الموصلات الفائقة أو حتى في صنع الحاسوب الكمي، ولكن البحث الحالي الذي يكشف أسرار حالات المادة الغريبة هو بفضل جهود هؤلاء العلماء.

والآن بعد قراءة البيان الصحفي لنوضح بعض المفاهيم:

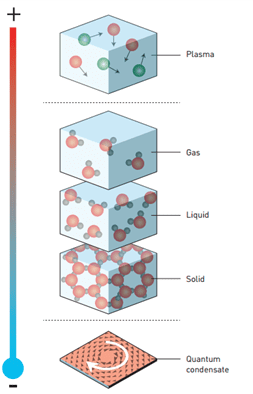
من المعروف أن حالات المادة العادية هي: صلبة، سائلة، غازية. والمادة يُمكن أن تكون في أكثر من حالة؛ فمثلًا الماء يكون سائلا أو غازا أو صلبا، والتغير في حالات المادة أو الـ Phase Transition شغَل بالَ علماء الفيزياء لسنوات طويلة، فيُمكنك تحويل حالة المادة بتغيير درجة الحرارة. فعلى سبيل المثال؛ لتحويل الماء السائل إلى غاز عليك تسخين السائل لدرجة حرارة معينة ،بعدها يتحول إلى بخار. ولتُعيد البخار إلى الحالة السائلة يجب تكثيفه بتقليل درجة الحرارة.

حسنا، هذا ربما تكون قد درسته في المدرسة أو الجامعة. ولكن ما لم تدرسه (أو مر عليك مرور الكرام) هو أنه إذا قُمنا بتبريد المواد إلى درجات حرارة منخفضة للغاية سنحصل على حالة غريبة من المادة. فعلى سبيل المثال؛ بعض المواد عند تبريدها لدرجات منخفضة تقترب من -273 سيلزيوس تختفي منها المقاومة الكهربية وتصبح موصلات فائقة. وأيضًا عند تبريد الهيليوم إلى -271 سيلزيوس يُصبح مائعا فائقا تختفي منه اللزوجة.

والآن لموضوع جائزة نوبل:

أحد أسباب منح جائزة نوبل اليوم لثاولز وكوسترليتز هو دراستهم لعملية تحوُّل المادة أو تحول الطور (Phase Transition) في الطبقات الرقيقة. ففي السابق كان العلماء يعتقدون أن نتيجة الاضطرابات الحرارية ستدمر النظام المتراصف في الطبقات الرقيقة، حتى عند الصفر المطلق، وإذا غاب النظام فلا يوجد تحول في الطور.

ولكن ثاولز وكوسترليتز قاما بدراسة هذا الموضوع ووجدا باستخدام الطوبولوجي أنه يوجد تحول في الطور، ولكنه ليس تحولا عادياً كالذي يحدث في المواد العادية، ولكنه شكل مختلف من أشكال التحول.

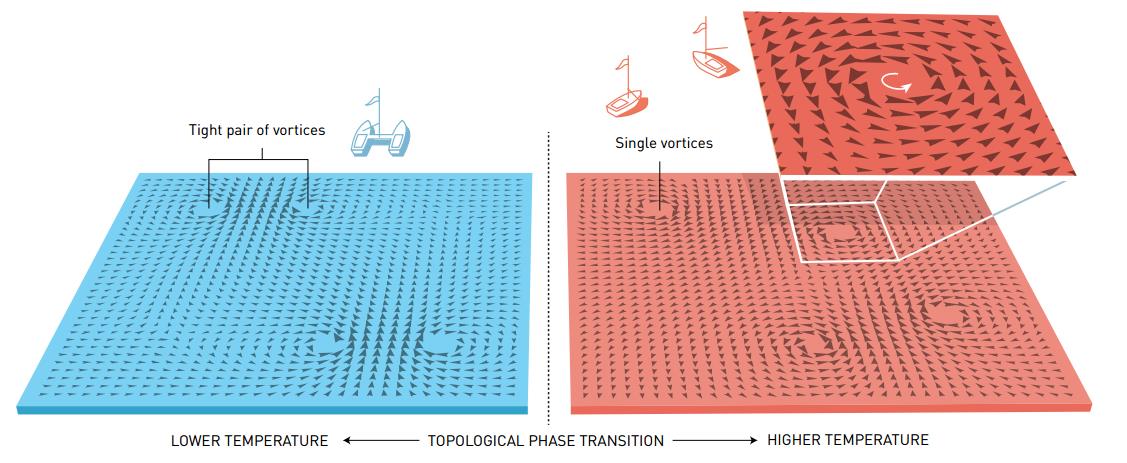
في المواد المسطحة (ثنائية الأبعاد) توجد دوامات صغيرة. عند الدرجات المنخفضة تكون هذه الدوامات أزواجًا مترابطة، وإذا رُفعت درجة الحرارة تنفصل هذه الأزواج بعضها عن بعض، وهذا هو التحول في الطور. ولنعود ونتذكر البيان الصحفي: «فالطوبولوجي (Topology) هو فرع الرياضيات الذي يصف الخواص التي تتغير فقط بخطوات محددة»، هذا هو التحول الطوبولوجي في الطور.

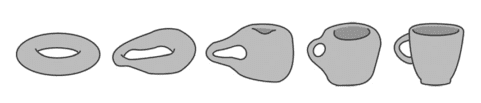
فالطوبولوجي هو العلم الذي يدرس الخواص التي تظل ثابتة حتى ولو مُطَّ الجسم أو شُوِّه، ولكن تتغير إذا قُسِّم. فمثلا الكرة والمكعب متكافئان طوبولوجيًا، والطوق وكوب القهوة متكافئان طوبولوجيًا أيضًا، فيُمكن تحويل الطوق إلى كوب قهوة والحفاظ على عدد الثقوب ثابتًا.

هذا ليس كل ما في الموضوع، ففي الثمانينيات قام ثاولز أيضًا بتفسير تجربة أجراها العالم الألماني كلاوس فون كليتزينج (Klaus von Kliztzin) -الحائز أيضًا على جائزة نوبل-. هذه التجربة أدت لظهور ما يعرف بتأثير هول الكمي (Quantum Hall Effect).

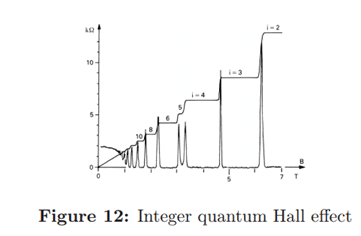
حين وضع كليتزينج طبقة رقيقة من مادة موصلة بين شريحتين من مادة شبه موصلة وتم تبريدها لدرجات حرارة منخفضة جدًا وتعريضها أيضًا لمجال مغناطيسي قوي، وجد كليتزينج أن توصيلية المادة الرقيقة تتغير بقيم محددة، وهذا غير عادي في الفيزياء. ولوحظَت النتيجة نفسها أيضا حتى مع تغير شدة المجال المغناطيسي ودرجة الحرارة وكمية الشوائب في المادة شبه الموصلة، فعند تغيير المجال المغناطيسي بقدر معين تتغير التوصيلية، ولكن بخطوات ثابتة.

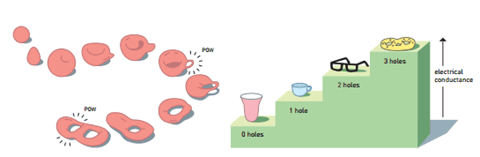
هذه الظاهرة كانت غريبة ولا يُمكن تفسيرها بالفيزياء المعروفة في ذلك الوقت، لذا جاء ثالوز بعصاه السحرية المسماة بالطوبولوجي وقدم الحل.

الإلكترونات تتحرك بحرية في الطبقة الموصلة الموجودة بين المادة الشبه الموصلة، وهي تكوّن ما يُطلق عليه المائع الطوبولوجي الكمي (Topological Quantum Fluid). هذا المائع أو الغاز يمتلك خواصًا غريبة على المستوى الكمي. هذه الخواص لا يمكن التأكد من أنها طوبولوجية إلا إذا نظرنا إلى المائع ككل، والطريقة الوحيدة للتأكد من ذلك هو قياس التوصيلية.

وإنجاز آخر قام به دانكن هالدين؛ أنه بيّن أن الموائع الطوبولوجية تتواجد أيضًا في الطبقات الرقيقة من المواد شبه الموصلة، حتى في غياب المجال المغناطيسي.

أدت هذه الأبحاث ودمج الطوبولوجي بفيزياء المادة المكثفة إلى ظهور أبحاث أخرى عن أنواع جديدة من المواد الطوبولوجية؛ منها: العوازل الطوبولوجية والموصلات الفائقة الطوبولوجية والعديد من المواد الغريبة التي ستساهم بالتأكيد في تقدم البشرية.

إعداد: Ahmed Mohamed
مراجعة: علي أدهم

مصادر:

(2016). Nobelprize.org. Retrieved 4 October 2016, from https://www.nobelprize.org/nobel_prizes/physics/laureates/2016/popular-physicsprize2016.pdf

Thouless, D., Kohmoto, M., Nightingale, M., & den Nijs, M. (1982). Quantized Hall Conductance in a Two-Dimensional Periodic Potential.Physical Review Letters, 49(6), 405-408. doi:10.1103/physrevlett.49.405

Avron, J., Osadchy, D., & Seiler, R. (2003). A topological look at the Quantum Hall effect. Phys. Today, 56(8), 38-42. doi:10.1063/1.1611351