المجسمات الأفلاطونية- Platonic solid

في الفضاء ثلاثي الأبعاد تتكون المجسمات الأفلاطونية أو المجسمات المنتظمة من مضلعات منتظمة متطابقة ويمثل كل مضلع من هذه المضلعات أحد أوجه المجسم ويسمى المجسم بعدد الأوجه المكونة له, وهناك خمسة مجسمات تحقق هذه الشروط وتسمى بالمجسمات الأفلاطونية وهى كما يلي:

1. رباعي الأوجه أو الهرم الثلاثي- Tetrahedron

1. سداسي الأوجه أو المكعب- hexahedron

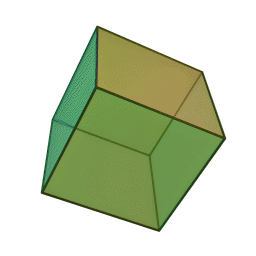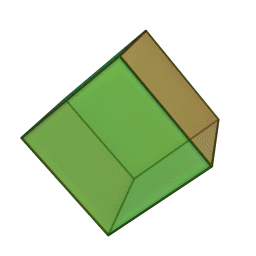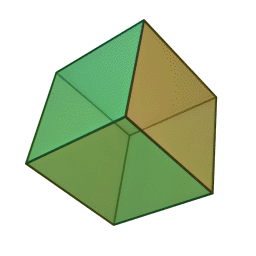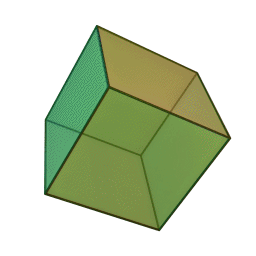
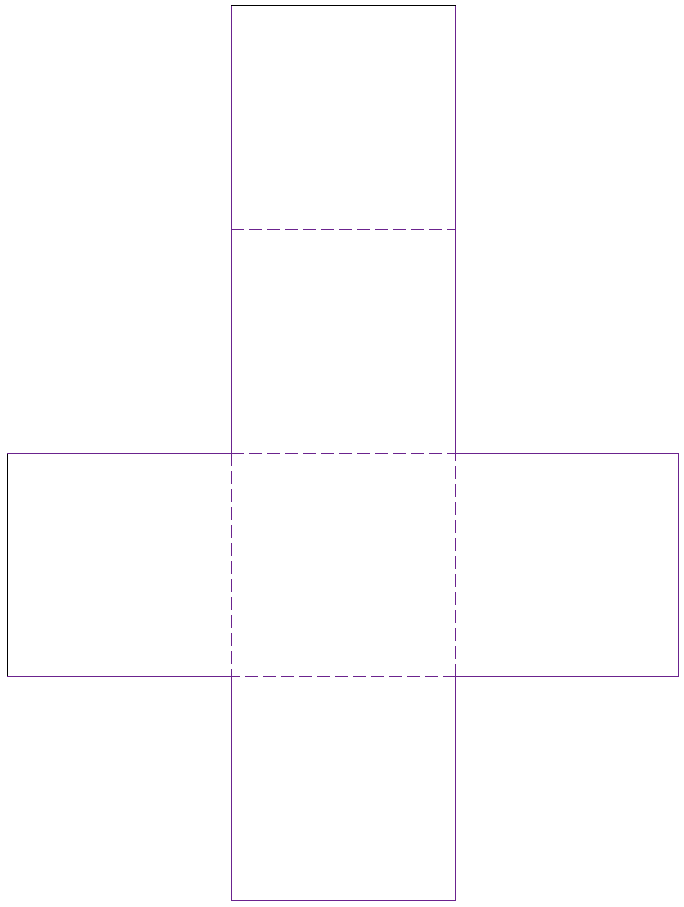
1. ثماني الأوجه – Octahedron

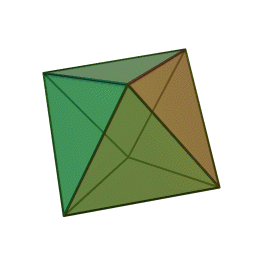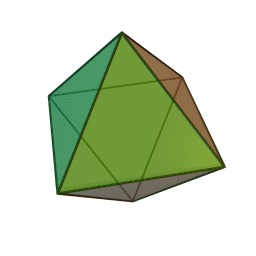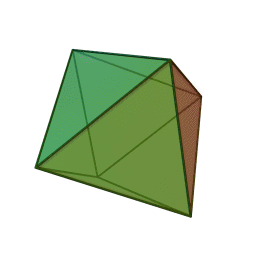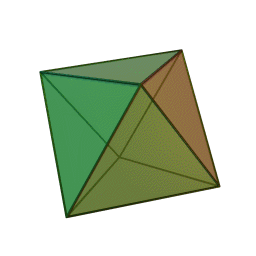
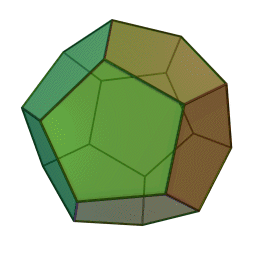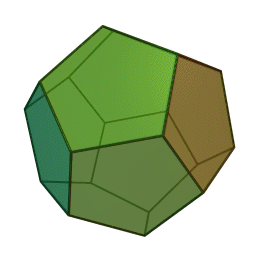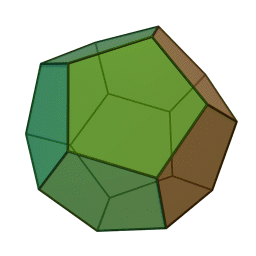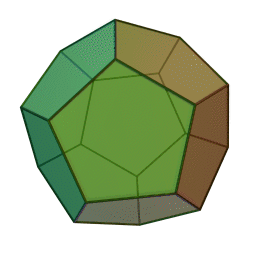
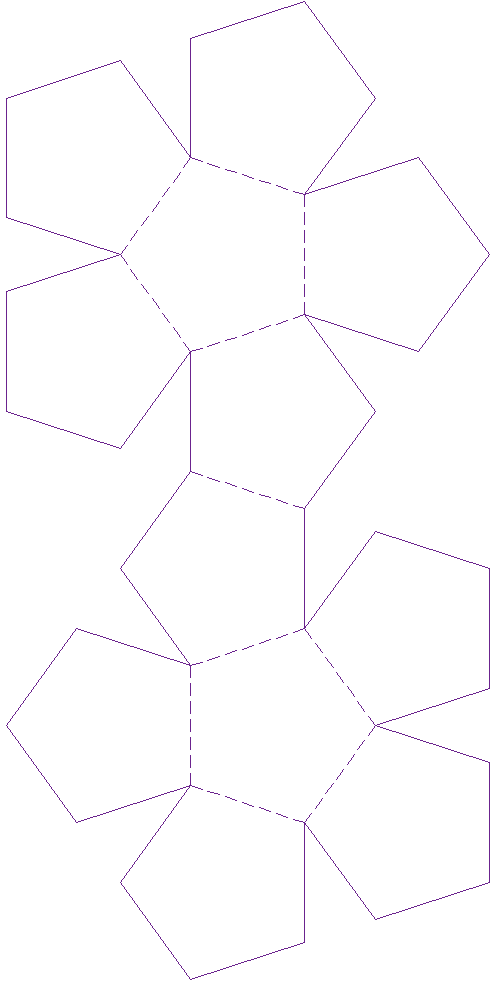
1. المجسم ذو الاثنا عشر وجه- Dodecahedron

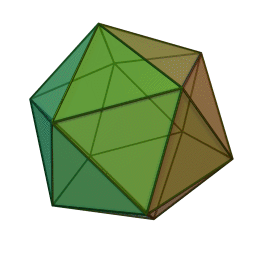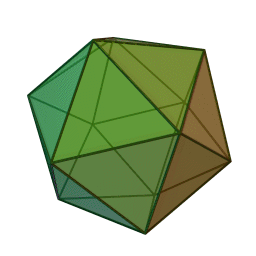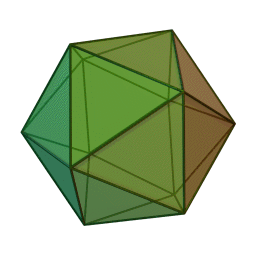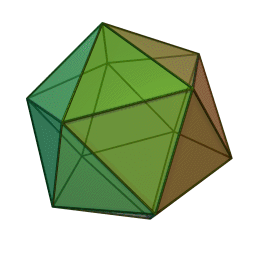
1. المجسم ذو العشرين وجه- Icosahedron

لقد قام علماء الهندسة بدراسة الجمال الرياضي والتماثل في هذه المجسمات لألاف السنين. وقد أطلقوا عليها اسم الفيلسوف اليوناني القديم أفلاطون هو الذي وضع الأساس النظري لها في حواره تيموس- Timaeus, عام 360 قبل الميلاد, والذي يرتبط بالعناصر الأولية الأربعة (الأرض, الهواء, الماء, النار) مع مجسم من المجسمات المنتظمة.

ارتبطت الأرض مع المكعب، الهواء مع المجسم الثماني، المياه مع المجسم العشريني ، والنار مع رباعي الأوجه.

Polyhedron		Vertices عدد الرؤوس )V(	Edges عدد الأحرف )E(	Faces عدد الأوجه)F(
tetrahedron		4	6	4
hexahedron (cube)		8	12	6
octahedron		6	12	8
dodecahedron		20	30	12
icosahedron		12	30	20

والعجيب في هذه المجسمات أنها تحقق ما يسمى صيغة أو معادلة أويلر Euler’s formula :

V   +   F   –   E  =   2

بمعنى أنه عند جمع عدد الرؤوس V مع الأوجه F ثم نطرح منهم عدد الأحرف E  فإن الناتج يكون دائما 2 مع المجسمات الخمسة.

وقد تزداد دهشتك وتعجبك وانبهارك بهذه المجسمات الرائعة عندما تعرف أن معادلة أويلر تكون صحيحة مع هذه المجسمات حتى بعد قطع أحد الرؤوس أو كل رؤوس المجسم.

ترجمة: Mahmood Yosef Mahmood

مراجعة: Abrar mahrous

تصميم:Ahmed  EL-tobshy

المصدر:

https://goo.gl/dL0IzI

https://goo.gl/l9B7XC

https://goo.gl/k7zi1h

#الباحثون_المصريون