بعد ما تعرضنا في الموضوع السابق لمكونات وخصائص الأنظمة المنطقية، واستعرضنا معًا تاريخ بدايات المنطق، نصل معًا إلى أول نظام منطقي فى التاريخ، وهو المنطق الصوري لأرسطو الذى عرضه أرسطو فى كتابه الشهير (The Organon).ويسمى نظام أرسطوبـ(Term Logic).
ويقوم هذا النظام على تحليل الأحكام (Judgments)إلى قضيتين (Premises) أو أكثر، كل منهم تتكون من مصطلحين نوعيين (Categorical Term) يسميان موضوع (Subject) ومحمول(Predicate)،وهم مرتبطان بعلاقة منطقية من بين4 أشكال للعلاقات المنطقية (Logical Form)، على شرط أن يكون هناك مصطلح مشترك بين القضيتين (Middle term)، ثم يتم استنتاج القضية الثالثة (العلاقة بين المصطلحين الفريدين فى المقدمتين “طرفى القضية”) الناتجة عن القضيتين الأوليتين عن طريق واحدة من 24 قاعدة للاستدلال (Inference Rules)حددها أرسطو،وفيما يلي مثالًا وتحليله:
«كل الفلاسفة مفكرون – بعض الإغريق فلاسفة – إذًابعض الإغريق مفكرون»
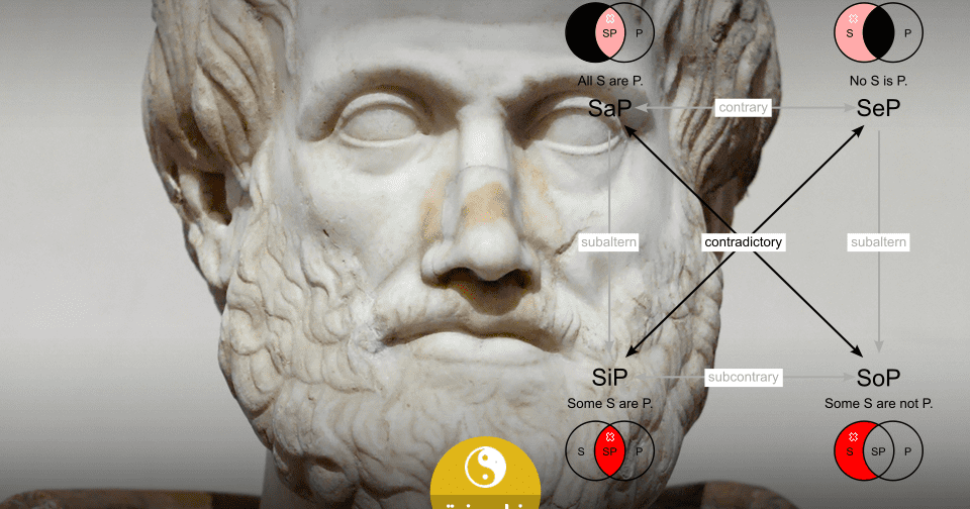
- يوجد 4 أشكال منطقية محددة (Logical Form) وقد تم رسمها فى ما يعرف بمربع أرسطو (The Square of Opposition) والذى يظهر إرتباطات الأشكال المنطقية الأربعة ببعضها البعض، وتعدأول خطوة للحصول على المقدمتين هي ترجمة جمل اللغة العادية الى واحدة من الجمل التالية:
أ. كلية مثبتة (كل س هو ص) مثل (كل الفلاسفة مفكرون) ويسمى هذا الشكل المنطقى (A)
ب. خاصة مثبتة (بعض س هو ص) مثل (بعض الفلاسفة مفكرون) ويسمى (I)
ج. كلية منفية مثل (كل س ليس هو ص) مثل (كل الفلاسفة ليسوا مفكرين) ويسمى (E)
د. خاصة منفية مثل (بعض س ليس هو ص) مثل (بعض الفلاسفة ليسوا مفكرين) ويسمى (O)
- مكونات الجمل وتنقسم إلى ثوابت منطقية (Logical Constants) و قيم متغيرة وهى:
أ. (كل وبعض) هي محددات للكمية التي تنطبق عليها الجملة، وهي من الثوابت المنطقية التي لا تتغير من جملة لأخرى بل يمكن أن تحذف إذا كان المتغير اسم محدد (أحمد مثلا).
ب. (س وص) هي متغيرات أشترط أرسطو أنها لابد وأن تعبرعن شئ فى الواقع فقد تحمل أي أسماء (أحمد مثلا) أو أنواع (إنسان مثلا) أو صفات (ذكي مثلا)، وأول متغير والذى يخضع للتحديد يسمى “موضوع” (Subject)، وثاني متغير يسمى “محمول” (Predicate) والمتغير الثالث هو المشترك بين القضيتين (Middle term).
ج.( هو وليس هو) هي العلاقة أو النسبة بين الموضوع والمحمول أي بين أول متغير وثانى متغير. وتستعمل الضمائر باختلافاتها وفقًا لنوع الموضوع (مثلا هى وليس هى ….إلخ.)
- كتب أرسطو الصور الممكنة للعلاقات بين الموضوع والمحمول والمشترك وأسماها أشكال الاستدلال (Figures). وفيها ثبت أرسطو النتيجة (القضية الثالثة) على الشكل (موضوع- محمول) وتنوعت أشكال المقدمات بكل صورها كالتالى:
أ. قضية أولى (مشترك- محمول) وقضية ثانية (موضوع- مشترك) وسميت هذه العلاقة (الشكل الأول)*مثال: كل الفلاسفة مفكرون – بعض الإغريق فلاسفة
ب. قضية أولى (محمول- مشترك) وقضية ثانية (موضوع- مشترك) وسميت هذه العلاقة (الشكل الثانى)
*مثال: كلالمفكرين فلاسفة – بعضالإغريقفلاسفة
ج. قضية أولى (مشترك – محمول) وقضية ثانية (مشترك – موضوع)وسميت هذه العلاقة (الشكل الثالث)
*مثال: كلالفلاسفةمفكرون – بعضالفلاسفة إغريق
د. قضية أولى (محمول – مشترك) وقضية ثانية (مشترك – موضوع)وسميت هذه العلاقة (الشكل الرابع)
*مثال: كلالمفكربن فلاسفة – بعضالفلاسفةإغريق
- قام أرسطو بحساب كل الصور (syllogism) الممكنة فوجد أن لديه الآن 4 أشكال استدلالية * 4 أشكال منطقية للقضية الأولى * 4 أشكال منطقية للقضية الثانية * 4 أشكال منطقية للنتيجة = 256 صورة. ويتم الرمز إليها بثلاث حروف كل حرف يمثل الشكل المنطقى لقضية من الثلاث قضايا ويتبعها رقم شكل الاستدلال،فمثلا الاستدلال التالي هو على شكل الاستدلال(رقم 1) وأول قضية على الشكل المنطقى (A) وثانى وثالث قضية على الشكل (I) فيرمز له بـ (AII-1)
كل الفلاسفة مفكرون- بعض الإغريق فلاسفة – إذًا بعض الإغريق مفكرون
- بحث أرسطو عن الصورالخاطئة منطقيًا(Invalid) بين الـ(256) صورة، حيث توجد صور نتيجتها الثالثة لا تستنتج منطقيًا من المقدمتين: ومثال على ذلك، الاستدلال التالي على الشكل (AIE-1)
كل الفلاسفة مفكرون- بعض الإغريق فلاسفة- كل الإغريق ليسوا مفكرين
- أخذ أرسطو يضع أمثلة تثبت خطأ بعض الصور المنطقية، مثل المثال السابق، وسمى تلك الطريقة بـ (Reductio Ad Impossibile) حتى أثبت خطأ 232 صورة وتبقى لديه 24 صورة فقط:
أ.على شكل الاستدلال الأول (AAA) (EAE) (AII) (EIO) (AAI) (EAO)
ب.على شكل الاستدلال الثانى (EAE) (AEE) (EIO) (AOO) (AEO) (EAO)
ج. على شكل الاستدلال الثالث (IAI) (AII) (OAO) (EIO) (AAI) (EAO)
د. على شكل الاستدلال الرابع (AEE) (IAI) (EIO) (AEO) (EAO) (AAI)
- وجد أرسطو أن كل الصور التي على شكل الاستدلال الأول (Figure 1) من الـ(24) صورة هي من البديهيات (Axioms)وهيجمل يظهر صدقهابدون أيإثبات بل بمجرد أن يعقلها الشخص.
- ثم أخذ يثبت بقية الصور الصحيحة منطقيًابأن يحولها لإحدى الصور التي على شكل الاستدلال الأول (Figure 1)،وبذلك فقد تحولت الصور الصحيحة منطقيًا من أشكال الاستدلال الأخرى لنظريات (Theorems) فى نظام أرسطو المنطقى، مثال:
(بعض س هو ص) تتحول إلى (بعض ص هو س) – مثال (بعض الفلاسفة مفكرون) و(بعض المفكرون فلاسفة)
(كل س هو ص) تتحول إلى (بعض س هو ص) – مثال (كل الفلاسفة مفكرون) و(بعض الفلاسفة مفكرون)
(كل س ليس هو ص) تتحول إلى (كل ص ليس هو س) – مثال (كلالقططليسوا كلاب) و(كلالكلاب ليسوا قطط)
- وضع أرسطو قواعد الاستدلال (Inference Rules) في نظامه المنطقي فى صورة(24) قانونًا، بمعنى أنه إذا استطعت ترجمة جمل اللغة العاديةإلى قضيتين كل منهما هي مقدمة من مقدمات الصور الـ(24)السليمة منطقيًا، فيمكنك بطريقة ميكانيكية استنتاج القضية الثالثة وأنت متأكد أنها صحيحة منطقيًا، الجدير بالذكر أن فى العصور الوسطى كانت كل صورة من الـ(24) الصحيحة تسمى على اسم فتاة لسهولة الحفظ،نعم! كان فلاسفة العصور الوسطى يحفظون الصور ال24 حفظا تامًا ويعتبرونها أساس أى استدلال سليم.
- الجدير بالذكر أن المنطق الرياضى جعل الصور الصحيحة 15 صورة فقط، وحذف كل الصور التي ظهرت بها “بعض” (الأشكال المنطقية O,I) في النتيجة بدون أن تظهر في أي من المقدمات؛ لأن المنطق الرياضي يعتبر أن “بعض” تعنى أنه لابد وأن يكون هناك شيئًا موجودًا واقعيًا (existential import)، على عكس “كل” التي قد تنطبق فى المنطق الرياضي على المجموعات الكلية الواقعية والخيالية التي قد لا تكون موجودة في الواقع مثل مجموعة طيور الرخ مثلًا، وبالتالي فلا يوجد “بعض” مع المجموعات الخالية لكن يوجد “كل”، فلابد إن أردت استعمال “بعض” فى النتيجة، أن أحدد في المقدمات أن تلك المجموعة بعضها موجود، نذكر أن ذلك الشرط يعتبرعكس ما قال به أرسطو أن المتغيرات هى مجموعات واقعية فقط وسنناقش هذا بالتفصيل عندما نصل للمنطق الرياضي.
وبهذا نكون انتهينا من تحليل المنطق الصوري الأرسطى الذي سيطر على العالم لقرابة 1900 عامًا، ولكن مع انصهار المنطق الأرسطي في الفلسفة الإسلامية بدأت بعض عيوبه في الظهور قبل أن تتبلورعلى يد بعض فلاسفة القرون الوسطى في أوروبا، ظهر أول عيب وهو قصور المنطق الأرسطي الشديد في التعبير عن حالات واقعية كثيرة مثل:
- الحالات الزمنية (Temporal) التي أضافها ابن سينا كعامل منطقيفي المنطق الصوري عن طريق استخدام مفاهيم مثل “في كل الأوقات” أو “في بعض الأوقات” أو “في معظم الأوقات” وهو النظام المنطقي الذي انتقل لأوروبا فى القرون الوسطى بإسم (Ampliation) والذي تطور بقوة في الستينيات من القرن العشرين (Modal Logic).
- الخصائص الوجودية في حالة الأفكارالمجردة، بمعنى أن المنطق الأرسطي لا يستطيع التعبيرعن الأفكار المجردة لأن الشكل المنطقي للقضايا يستلزم مصطلحات نوعية لأشياء موجودة واقعيًا، فلا يمكن مثلًا التعبير عن فكرة مجردة كـ”الكوب كلمة تتكون من ثلاثة حروف” لأن الكوب فى المنطق الأرسطي هو الشيء الذي نشرب منه.
- الشرطية، تلك الفكرة المنطقية التي أبدعها «الرواقيون»، ويعتبر وليم الأوكامي (William of Ockham) هو أول من وضع نظام يزاوج بين الشرطية والمنطق الصورى في كتابه كتابه (Summa Logicae).
- الروابط المنطقية (Logical Connectives) مثل “و” (and)، “أو” (or) وغيرهما.
ثم ظهرت المشكلة القاتلة للمنطق الأرسطي، ونلاحظ أن كل الأشكال المنطقية للقضايا يوجد بها محددات للكمية ولكن عددها واحد دائمًا وبالتالي إذا أردت استعمال محددتين للكمية أو أكثر فلن أستطيع، مثال “كل الفئران تخاف من بعض القطط” ومثال أخر “بعض الأشخاص لديهم كل الحظ”، وقد سميت تلك المشكلة بـ (Multiple Generality).
هذا الضعف الشديد فى منطق أرسطو، جعل الكثير ينقدونه نقدًاقائمًا على النظرة التجريبية (Empirical) كنقد«ابن تيمية»بأن المنطق تحصيل حاصل لا يحتاج لقواعد ومثله نقد «جون لوك» الفيلسوف الإنجليزى الشهير، والذي يعتبر أبو التجريبية، عام 1675 فقال “كأنك تقول أن الله لم يدخر وسعًافي جعل الإنسان مجرد مخلوق يمشي على قدمين، وترك لأرسطو مهمة أن يجعله عاقل.”وأدى ذلك النقد التجريبي لبزوغ طريقة جديدة من المنطق بعيدًا عن الاستدلال وهو الاستقراء (Inductive Logic)على يد «فخر الدين الرازى» والذى تحول إلى نظام منطقي كامل على يد«فرانسيس بيكون» والفيلسوف البريطاني الشهير«جون ستيوارت مل».
ورغم كل تلك العيوب، استطاع المنطق الأرسطي، بعد إضافة الأفكار السابق ذكرها له، البقاء كالنظام المنطقي الأوحد في أوروبا،ولكن ظلت المشكلات الأساسية في المنطق الأرسطي بلا حل وخصوصًا مشكلة (Multiple Generality)، لأن الحل كان يكمن فى تزاوج الرياضيات والمنطق. فكان لابد من الإنتظار حتى يأتي رياضي عقلاني منطقي يضع ثاني خطوات التخلص من طريقة الاستنباط الأرسطية وكان هذا الرياضي هو «ليبنتز» الذي وضع أساسيات المنطق الرياضي ولكن سنترك هذه القصة للمرة القادمة إن شاء الله.
إعداد: Ali Reda
المصادر والمراجع:
Simple Formal Logic byArnold vander Nat
Introductionto Logic by Harry J. Gensler
The Development of Logic by William Kneale and Martha Kneale
#الباحثون_المصريون