منحت الأكاديميّة الملكيّة السويديّة للعلوم جائزة نوبل في الفيزياء لعام 2021 للفيزيائيّ الإيطاليّ جورجيو باريسي من جامعة سابينزا الإيطاليّة في روما عن إسهاماته في فهم التفاعلات الفوضوية والتقلّبات الحادثة في الأنظمة الفيزيائيّة بدءًا من الأنظمة الذرّية الصغيرة وحتّى الأنظمة الفيزيائيّة الكبيرة بحجم الكوكب، مناصفة مع كلّ من الفيزيائيّ اليابانيّ سيوكورو مانابي من جامعة برينستون بالولايات المتّحدة الأمريكيّة، والفيزيائيّ الألمانيّ كلاوس هاسلمان من معهد ماكس بلانك للأرصاد الجويّة في مدينة هامبورغ بألمانيا عن إسهاماتهما في النمذجة الفيزيائيّة للمناخ على كوكب الأرض والتنبّؤ عالي الدقّة بالتغيّرات المناخيّة والاحتباس الحراري. تنطوي أعمال العلماء الثلاثة تحت مفهوم فيزياء الأنظمة المعقّدة التي يعتبر مجال المناخ مثالًا لأحد تطبيقاتها، والتي سنتناولها في هذا المقال بشيءٍ من التفصيل.

مفهوم فيزياء الأنظمة المعقّدة

نشأ مفهوم فيزياء الأنظمة المعقّدة نتيجةً لعجز الفيزياء التقليديّة وفيزياء الكمّ عن التنبّؤ بسلوك نظامٍ معيّنٍ انطلاقًا من دراسة سلوك كلّ جزءٍ من مكوّنات هذا النظام بمفرده، ففي بعض الأحيان تكون الخصائص الناشئة للأنظمة المعقّدة أكبر من مجموع أجزاء النظام الواحد، ممّا يتطلّب منّا اتّخاذ خطوةٍ إلى الوراء وإلقاء نظرةٍ عامّةٍ أكثر شموليّةً على النظام كلّه.

إنّ دراسة جزيء ماءٍ واحدٍ -على سبيل المثال- لا تفسّر وجود الماء في الحالة السائلة، ولا وجود بخار الماء في الحالة الغازيّة، ولا وجود الجليد في الحالة الصلبة. وهكذا تسعى فيزياء الأنظمة المعقّدة إلى دراسة قدرة المكوّنات الفرديّة لنظامٍ معقّدٍ كبيرٍ على العمل معًا لإحداث سلوكٍ فريدٍ من نوعه لا يمكن التنبّؤ به من خلال فهم سلوك كل جزءٍ من الأجزاء المكوّنة لهذا النظام على حدةٍ.

أما النظام المعقّد فهو ذلك النظام الذي يمكن إدراكه وقياسه من نواحٍ عديدةٍ بشكلٍ مباشرٍ ومن خلال دراسة الديناميكيّات الجماعيّة لكافّة مكوّناته. وهناك العديد من الأنظمة التي يمكن اعتبارها أنظمةً معقّدةً حولنا؛ بدءًا من جهازنا العصبيّ، ووصولًا إلى الأنظمة الاقتصاديّة، والاجتماعيّة، والأنظمة البيئيّة. تتميّز الأنظمة المعقّدة بالعشوائيّة والفوضى وصعوبة التنبّؤ بسلوكها على المدى الطويل. وإذا أخذنا المناخ كمثالٍ على هذه الأنظمة المعقّدة، فسوف نجد صعوبةً في التنبّؤ بحالة الطقس بعد عدّة عقودٍ من الآن، لأنّ التغيّرات المناخيّة تتّسم بالعشوائيّة، حيث تؤدّي الانحرافات الصغيرة في القيم الأوّليّة إلى اختلافاتٍ كبيرةٍ على المدى الطويل.

تاريخ فيزياء الأنظمة المعقّدة

تعود جذور الدراسات الحديثة للأنظمة المعقّدة إلى علم الميكانيكا الإحصائيّة الذي طوّره كلٌّ من جيمس سي. ماكسويل، ولودفيج بولتزمان، وچي. ويلارد چيبس ​​في النصف الثاني من القرن التاسع عشر، وهم من أطلقوا على هذا المجال اسم علم الميكانيكا الإحصائيّة في عام 1884.

كان تطوير مفهوم الميكانيكا الإحصائيّة ضروريًّا لوصف بعض الأنظمة، مثل الغازات والسوائل، والتي تتكوّن من أعدادٍ هائلةٍ من الجسيمات. بحيث يمكن باستخدام هذه الطريقة أن نأخذ الحركات العشوائيّة للجسيمات بعين الاعتبار، وكانت الفكرة الأساسيّة في الميكانيكا الإحصائيّة هي حساب متوسّط ​​تأثير الجسيمات بدلًا من دراسة كلّ جسيمٍ على حدةٍ. فعلى سبيل المثال، تُعتبر قيمة درجة حرارة الغاز معيارًا لمتوسّط ​​قيمة طاقة جزيئات الغاز. حقّقت الميكانيكا الإحصائيّة نجاحًا كبيرًا، إذ قدّمت تفسيرًا ميكروسكوبيًّا للخصائص الماكروسكوبيّة في الغازات والسوائل، مثل درجة الحرارة والضغط.

يمكن النظر إلى جزيئات الغاز باعتبارها كراتٍ صغيرةً تطير بسرعةٍ تزداد كلّما ارتفعت درجات الحرارة. وحينما تنخفض درجة الحرارة أو يزداد الضغط، تتكثّف الكرات أوّلًا لتصبح سائلًا، ثمّ تتحوّل إلى مادّةٍ صلبةٍ، وغالبًا ما تكون هذه المادّة الصلبة على هيئة بلّورةٍ، حيث تترتّب الكرات في شكلٍ منتظمٍ. ولكن، عندما يحدث هذا التغيير بسرعةٍ، فقد تتّخذ الكرات أشكالًا غير منتظمةٍ لا تتغيّر حتّى إذا تمّ تبريد السائل أو ضغطه، أو تبريده وضغطه معًا. وإذا كرّرنا التجربة، فإنّ الكرات سوف تتّخذ شكلًا جديدًا، على الرغم من حدوث التغيير بذات الطريقة تمامًا. فلماذا تكون النتائج مختلفة في كلّ مرّةٍ؟

يمكن اعتبار هذه الكرات المضغوطة في المثال السابق نموذجًا بسيطًا لموادّ مثل الزجاج العاديّ والموادّ الحبيبيّة، مثل الرمل أو الحصى. ولكن كان تركيز جورجيو باريسي خلال أبحاثه على نوعٍ مختلفٍ من الموادّ، وهو ما يُسمّى بالزجاج الدوّار، وهو نوعٌ من السبائك المعدنيّة التي تترتّب فيها الذرّات بحيث تُغيّر من الخصائص المغناطيسيّة للمادّة بطرقٍ عشوائيّةٍ ظاهريًّا لطالما حيّرت العلماء؛ بينما تمكّن باريسي في عام 1980، عن طريق استخدام الرياضيّات المعقّدة والنمذجة الحاسوبيّة، من اكتشاف أنماطٍ خفيّةٍ ونظريّاتٍ يمكنها أن تفسّر هذا السلوك، كما يمكن تطبيقها في العديد من مجالات البحث الأخرى مثل الرياضيّات، وعلم الأحياء، وعلم الأعصاب، والتعلّم الآليّ.

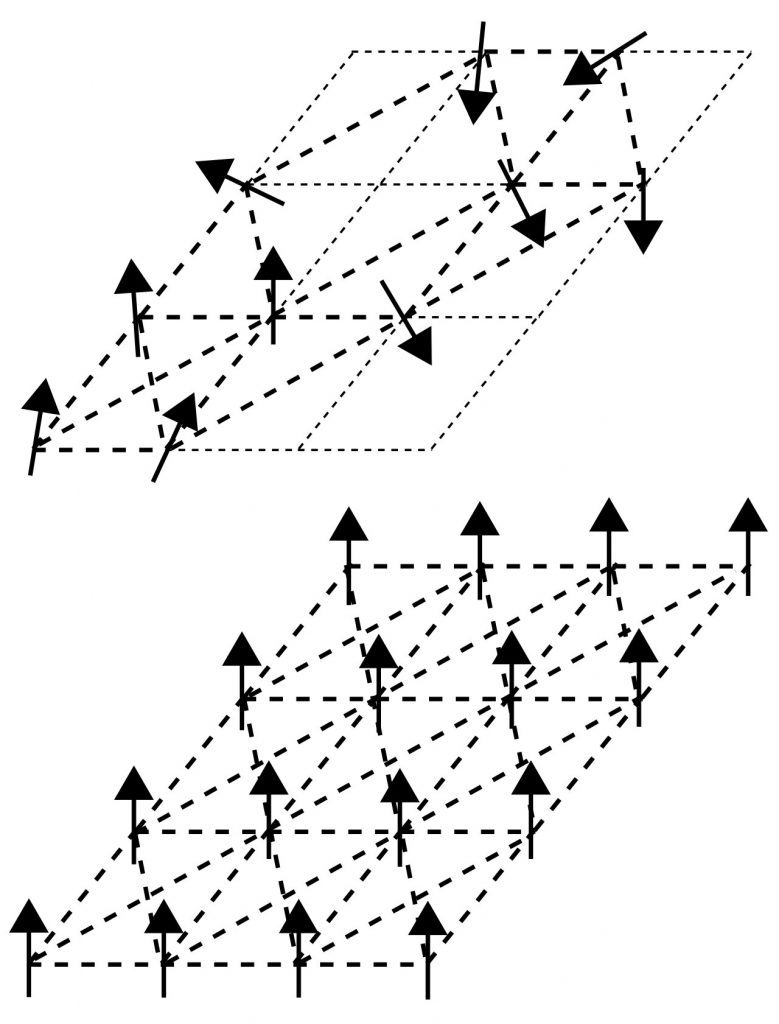
تتكوّن سبائك الزجاج الدوّار من خلط ذرّات الحديد بشكلٍ عشوائيٍّ في شبكةٍ من ذرّات النحاس. وعلى الرغم من وجود عددٍ قليلٍ من ذرّات الحديد في الخليط، إلّا إنّها تؤدّي إلى تغيير الخصائص المغناطيسيّة للمادّة بطريقةٍ جذريّةٍ ومحيّرةٍ للغاية. حيث تتصرّف كلّ ذرّة حديدٍ كمغناطيسٍ صغيرٍ، تتحرّك إلكتروناتها حركةً مغزليّةً، وتتأثّر بذرّات الحديد الأخرى القريبة منها. وتكون الحركة المغزليّة لجميع الإلكترونات في المغناطيس العاديّ في نفس الاتّجاه، ولكن في حالة الزجاج الدوّار، فإنّ بعض أزواج الإلكترونات تكون حركتها المغزليّة في نفس الاتّجاه، وبعضها في الاتجاه المعاكس.

يعتبر الزجاج الدوّار أحد أمثلة الأنظمة المضطربة حيث ينبغي على مختلف المكوّنات أن ترتّب نفسها بطريقةٍ تكون بمثابة حلٍّ وسطٍ بين عددٍ من القوى المتضادّة. ذكر جورجيو باريسي في مقدّمة كتابه عن الزجاج الدوّار، أنّ دراسة الزجاج الدوّار أشبه بمشاهدة المآسي الإنسانيّة في مسرحيّات شكسبير. إنّك إذا رغبت في تكوين علاقات صداقةٍ مع شخصين في ذات الوقت، وكلاهما يكره الآخر، فقد يكون الأمر محيّرًا. وكما هو الحال بصورةٍ أوضح في المأساة الكلاسيكيّة، حين يلتقي الأصدقاء والأعداء الألدّة على خشبة المسرح، فكيف يمكن تقليل التوتّر الموجود في جوّ المكان؟

تمثّل سبائك الزجاج الدوّار وخصائصها الغريبة نموذجًا للأنظمة المعقّدة. في سبعينيّات القرن العشرين، بحث العديد من الفيزيائيّين -ومن بينهم العديد من الحائزين على جائزة نوبل- عن طريقةٍ لوصف خصائص سبائك الزجاج الدوّار الغامضة والمحيّرة. كانت إحدى الطرق التي استخدموها هي حيلة النسخ المتماثلة، وهي تقنيّةٌ رياضيّةٌ تتمّ فيها معالجة العديد من النسخ والنسخ المتماثلة للنظام في نفس الوقت، بيد أنّ نتائج الحسابات الأصليّة جاءت غير مجديةٍ فيزيائيًّا.

حقّق جورجيو باريسي في عام 1979 تقدّمًا حاسمًا عندما أوضح كيف يمكن استخدام حيلة النسخ المتماثلة ببراعةٍ لحلّ مشكلة الزجاج الدوّار، حيث تمكّن من اكتشاف بنيةٍ خفيّةٍ في النسخ المتماثلة، ووجد طريقةً لوصفها رياضيًّا. استغرق الأمر سنواتٍ عديدةً حتّى تمّ إثبات صحّة حلّ باريسي رياضيًّا. استخدم باريسي خلال تلك السنوات طريقته في العديد من الأنظمة المضطربة وأصبحت طريقة باريسي بمثابة حجر الزاوية في نظريّة الأنظمة المعقّدة.

كانت اكتشافات باريسي الأساسيّة حول بنية سبائك الزجاج الدوّار متعمّقة جدًّا لدرجة أنّ تأثيرها لم يقتصر على مجال الفيزياء فحسب، بل أثّرت أيضًا على الرياضيّات، وعلم الأحياء، وعلم الأعصاب، والتعلّم الآليّ، حيث تتضمّن جميع هذه المجالات مشكلاتٍ مرتبطةً بالأنظمة المعقّدة بشكلٍ مباشرٍ.

درس باريسي أيضًا العديد من الظواهر الأخرى التي تلعب فيها العمليّات العشوائيّة دورًا حاسمًا في آليّة تكوين بنيتها التركيبيّة، وكيفية تطوّرها. وتعامل مع أسئلةٍ مثل: لماذا تتكرّر العصور الجليديّة بشكلٍ دوريٍّ؟ وهل يوجد وصفٌ رياضيٌّ أكثر عمومًا وشمولًا للفوضى والأنظمة المضطربة؟ وكيف تكون الأنماط الصوتيّة الناشئة عن تغريد سربٍ من آلاف الزرازير؟ قد يبدو هذا السؤال بعيدًا عن مسألة الزجاج الدوّار، إلّا إنّ معظم أبحاث باريسي قد تناولت كيف تؤدّي السلوكيّات البسيطة إلى سلوكيّاتٍ جماعيّةٍ معقّدةٍ. وهذا ما ينطبق على كلٍّ من الزجاج الدوّار وسرب الزرازير.