
في الهندسة الرياضية «مسألة أبولونيوس» هي عملية انشاء دوائر مماسة لثلاث دوائر معلومة في المستوى. وهي في الحقيقة تصف مدى براعة الرياضيين الإغريق في علم الهندسة المستوية، حيث صاغ أبولونيوس البيرجاوي (Apollonius of Perga) هذه المسألة وحلَّها في أحد أعماله التي ضاعت وهي «أطروحته-TANGENCIES». بشكلٍ عام فإنَّ ثلاث دوائر متباعدة لها ثمانية دوائر مختلفة تمسها. وهذه الدوائر الثمانية هي حل مسألة أبولونيوس.
يمكن تعميم هذه المسألة لتشمل إنشاء دائرة التماس لأي ثلاثة كيانات رياضية (النقطة والخط المستقيم والدائرة) مع التنويع فيما بينها لتعطي 10 مسائل تصف حالات تماس الدوائر مع أي ثلاثة كيانات رياضية معلومة.
-
هذه عشر حالات سنتحدث عنها وطرق حلَّها:
- انشاء دائرة مماسة لثلاث نقاط.
- انشاء دائرة مماسة لثلاثة مستقيمات.
- انشاء دائرة مماسة لنقطتين وخط مستقيم.
- انشاء دائرة مماسة لمستقيمين ونقطة.
- انشاء دائرة مماسة لنقطتين ودائرة.
- انشاء دائرة مماسة لدائرتين ونقطة.
- انشاء دائرة مماسة لمستقيمين ودائرة.
- انشاء دائرة مماسة لدائرتين وخط مستقيم.
- انشاء دائرة مماسة لنقطة ومستقيم ودائرة.
-
انشاء دائرة مماسة لثلاث دوائر معلومة.
-
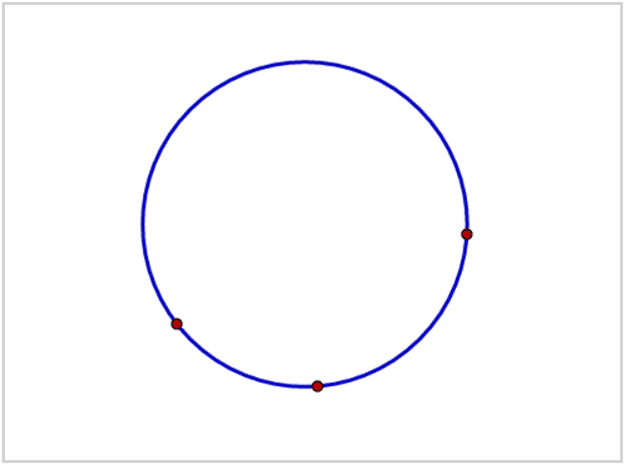
انشاء دائرة مماسة لثلاث نقاط (3 POINTS ppp):
*يوجد حل وحيد فقط لهذه المسألة.
-
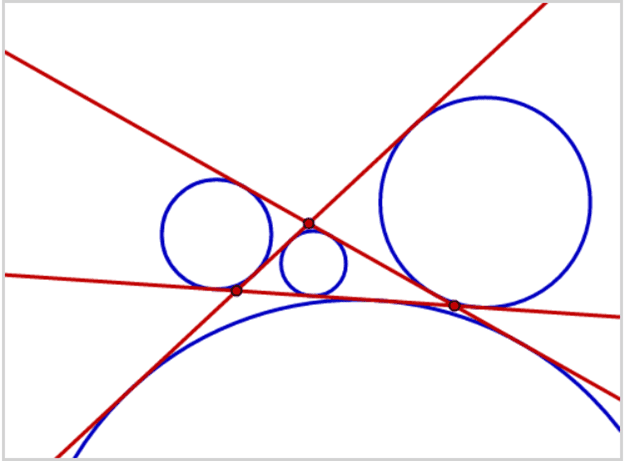
انشاء دائرة مماسة لثلاث خطوط (THREE Lines(LLL)):
*يوجد لهذه المسألة أربعة حلول على الأكثر.
-
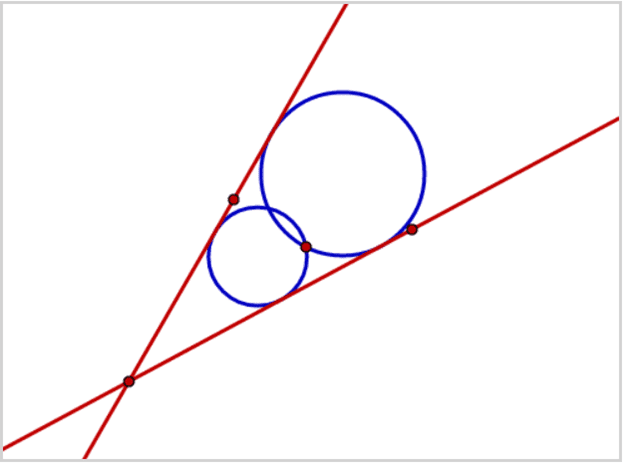
انشاء دائرة مماسة لنقطتين وخط مستقيم (PPL):
*يوجد لهذه المسألة حلَّان على الأكثر.
-
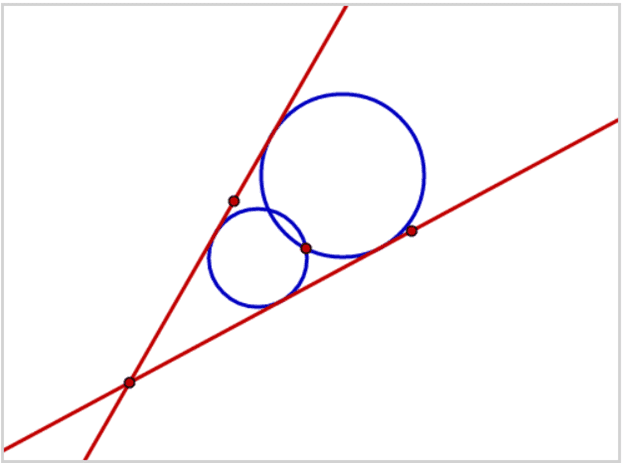
انشاء دائرة مماسة لمستقيمين ونقطة (PLL).
*يوجد لهذه المسألة حلَّان على الأكثر.
-
انشاء دائرة مماسة لنقطتين ودائرة (PPC):
*يوجد لهذه المسألة حلَّان على الأكثر.
-
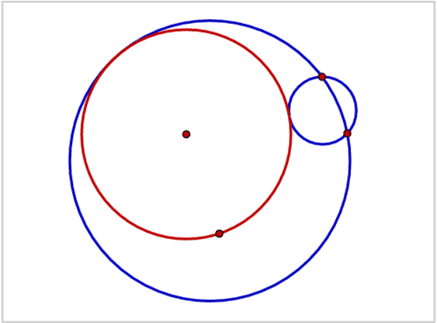
انشاء دائرة مماسة لدائرتين ونقطة (PCC):
*هذه المسألة لها أربعة حلول على الأكثر.
-
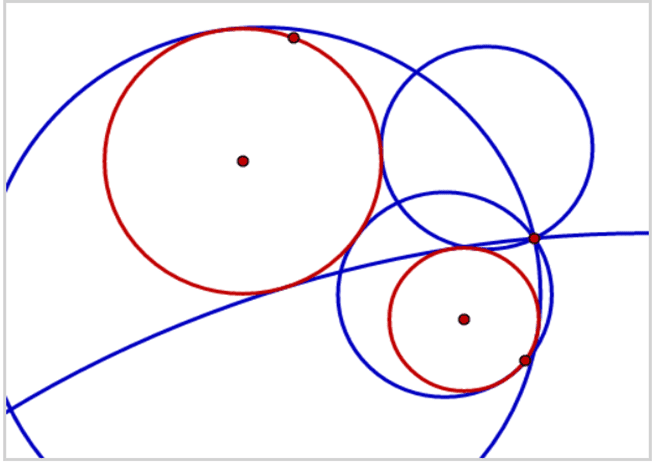
انشاء دائرة مماسة لمستقيمين ودائرة (LLC):
*يوجد لهذه المسألة ثمانية حلول على الأكثر.
-
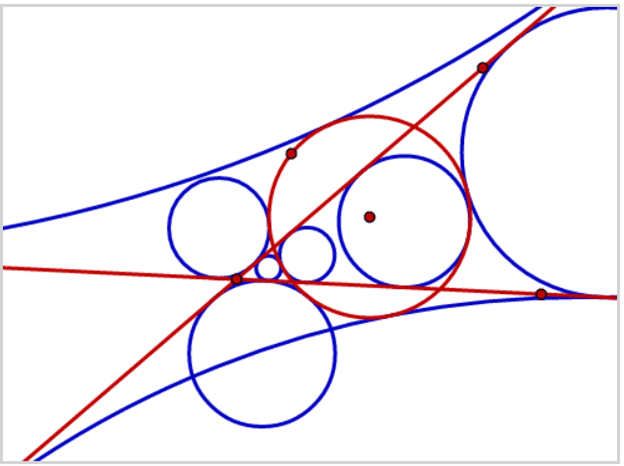
انشاء دائرة مماسة لدائرتين وخط مستقيم (LLC):
*يوجد لهذه المسألة ثمانية حلول على الأكثر.
-
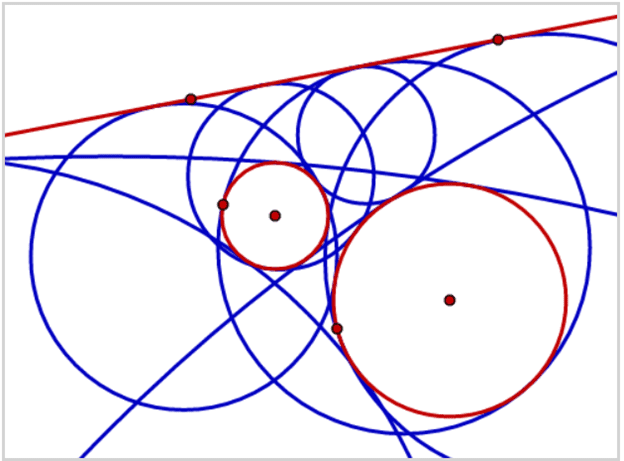
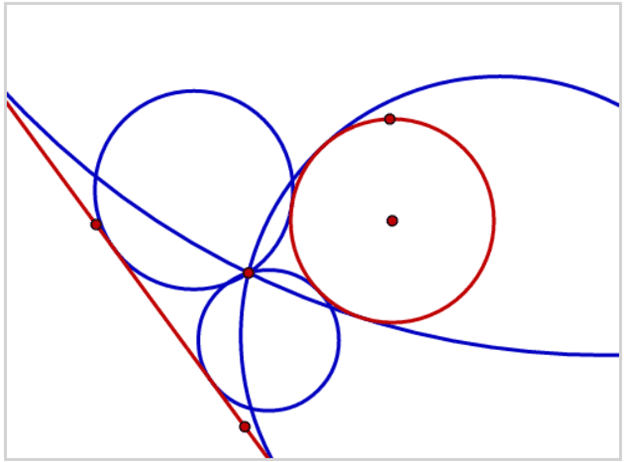
انشاء دائرة مماسة لنقطة ومستقيم ودائرة (PLC):
*يوجد لهذه المسألة أربعة حلول على الأكثر.
-
انشاء دائرة مماسة لثلاث دوائر معلومة (CCC):
*يوجد لهذه المسألة ثمانية حلول على الأكثر.
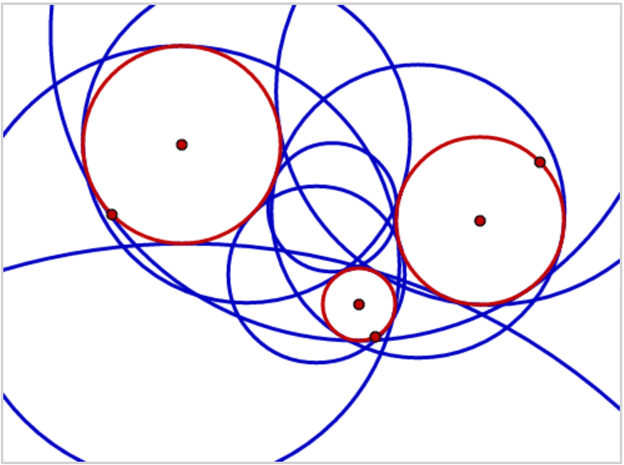
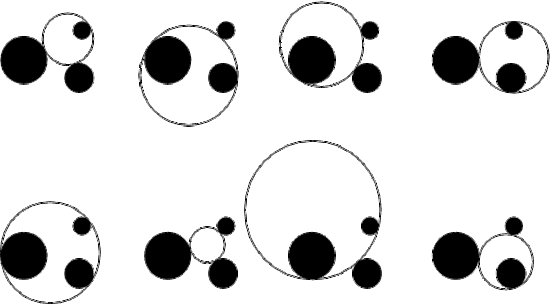


في الهندسة العكسية تُعامل الخطوط المستقيمة على أنَّها دوائر، وأنصاف أقطارها لانهائية ومركزها عند اللانهاية. بصفة خاصة إذا اعتبرنا الأضلاع الثلاثة لمثلث ما دوائر لانهائية المراكز والأقطار، فإنَّ «الدائرة الداخلية-incircle» و«الخارجية-excircle» للمثلث هي حلول لمسألة أبولونيوس. ومن الممكن ألَّا يكون لهذه المسألة أي حلول إذا كانت الدوائر الثلاثة المعطاة هي دوائر (concentric)؛ أي أنَّها تتشارك في نفس المركز. وكذلك من الممكن أن يكون لها عدد لانهائي من الحلول إذا كانت الدوائر الثلاثة تتلامس في نقطة معينة، والفضل في ذلك يرجع للرياضي«wilson stothers» لإظهاره تلك الإمكانية.
كما هو معتاد في الهندسة الإغريقية؛ فإنَّ عملية إنشاء هذه الدوائر تتم بالطرق التقليدية باستخدام المسطرة والفرجار.
إذا تلامست دائرتان في نقطة معينة فإنَّ نقطة التلامس تقع على الخط المستقيم المار بمركزيهما، حيث من الممكن أن تتلامس الدائرتان من الداخل أو من الخارج. يحدث ذلك تحديدًا عندما تقع أحد الدائرتين داخل الدائرة الأخرى. فإذا تلامسا خارجيًا كانت المسافة بين مركزيهما مساوية لمجموع نصفي قطريهما. أمَّا إذا تلامسا داخليًا: فإنَّ المسافة بين مركزيهما تساوي الفرق بين نصفي قطريهما.
*يمكننا استخدام الهندسة التحليلية لتوضيح حالات التماس لدائرة معينة مع 3 دوائر أخرى معلومة كالآتي:
فلنفترض أنَّ أنصاف أقطار الدوائر الثلاثة هي r1, r2, r3 وأنَّ مراكزها هي (x1, y1), (x2, y2), (x3, y3) على الترتيب. نبحث الآن عن الدائرة التي نصف قطرها r الذي هو غير معلوم ومركزها (x, y) الذي هو أيضًا غير معلوم. شرط التماس سيتحقق من خلال ثلاث معادلات تربيعية (من الدرجة الثانية) كالآتي:
| (x – x1)2 + (y – y1)2 = (r ± r1)2 (x – x2)2 + (y – y2)2 = (r ± r2)2 (x – x3)2 + (y – y3)2 = (r ± r3)2 |
كما تلاحظ هذه الثلاث معادلات خطية لثلاثة مجاهيل باللون الأحمر، كما أنَّ إشارات أنصاف أقطار الدوائر الثلاثة المعلومة في هذه المعادلات الثلاثة من الممكن اختيارها لتمثل كل واحدة منها معادلة منفصلة، إذًا فالمسألة من الممكن أن تحتوي على عدد 2*2*2 = 8 من الحلول. ولكن عدد هذه الحلول ليس 8 دائمًا. في الحالة العامة فإنَّ عملية طرح أحد هذه المعادلات الثلاثة من المعادلتين المتبقيتين ستنتج لنا نظامًا مكونًا من معادلتين خطيتين (2linear equations)، والذي فيه من الممكن التعويض عن قيم x و y بدلالة r وبعد التعويض سينتج لنا معادلة تربيعية أخرى بدلالة r ممَّا يعني أنَّه يمكننا استبدال كل القيم المجهولة x وy وr بدلالة الجذور التربيعية التي تمثل حلًا لهذه المعادلة، وبالتالي سنحصل على أطوال أنصاف الأقطار والمحل الهندسي لمراكز الدوائر المجهولة والتي تمس جميعها الدوائر الثلاث المعلومة التي تمثل حل مسألة أبولونيوس في النهاية؛ أيَّ أنَّه من الممكن تمثيل هذه الدوائر المتماسة باستخدام المسطرة والفرجار.
إعداد: Ahmed Hosiny
مراجعة لغوية: أمنية أحمد عبد العليم
تصميم: ندى أحمد

