تختصّ العلوم الميكانيكيّة -كفرعٍ من فروع الفيزياء- بالتّنبّؤ بحركة الأجسام في الزّمكان المحيط بها. ويمكن تحقيق ذلك عن طريق وضع نماذج تستطيع تفسير حركة تلك الأجسام من خلال الملاحظة وإيجاد نمطٍ ما للحركة. وتلك النّماذج لا تمثّل ترجمةً لحقيقة الكون وحركة الأجسام، ولكنّها تبسيطٌ للواقع كي نستطيع فهم حركة الأجسام من حولنا، ولخلق أنظمتنا الخاصّة.

وأيًّا كان النّموذج المتّبع، يتحتّم علينا اختيار نظام الإحداثيّات المناسب الّذي نستطيع من خلاله بناء القوانين والتّنبّؤ بحركة النّظام. فعلى سبيل المثال، في ميكانيكا نيوتن عادةً نلتزم بنظام الإحداثيّات الكارتيزيّ، وهنا يأتي نجاح قوانين نيوتن، فبقوانين بسيطةٍ للغاية أصبح لنا القدرة على فهم سلوك العديد من الأنظمة والأجسام إذا ما توفّرت لدينا بعض الشّروط الأوّليّة، وإذا ما استطعنا تحديد القوى الخارجيّة الواقعة على الجسم.

قوانين نيوتن

وتعتمد قوانين نيوتن في المقام الأوّل على السّبب والنّتيجة؛

• فالقانون الأوّل لنيوتن ينصّ على الآتي: «يظلّ الجسم على حالته الأصليّة، إمّا السّكون أو الحركة الثّابتة في خطٍّ مستقيمٍ ما لم يؤثّر عليه مؤثّرٌ خارجيٌّ يغيّر من حالته».
• بينما ينصّ القانون الثّاني على ما يلي: «إذا أثّرت قوّةٌ على جسمٍ فإنّها تكسبه تسارعًا، يتناسب طرديًّا مع القوّة وعكسيًّا مع الكتلة».
• أمّا القانون الثّالث فينصّ على أنّ «لكلّ قوّة فعلٍ قوّة ردّة فعلٍ مساويةٌ لها في المقدار ومعاكسةٌ في الاتّجاه يعملان على خطٍّ واحدٍ ويؤثّران على جسمين مختلفين»

وتتّبع قوانين نيوتن في ذلك منظور السّبب والنّتيجة، إذ تقدّم لك قوانين نيوتن قاعدةً صلبةً للتّعامل مع المتّجهات في الإحداثيّات الكارتيزيّة لبعض الأنظمة، مثل وصف موضع مقذوفٍ مُلقًى من مستوًى مائلٍ بزاويةٍ (α) وبزاوية إطلاقٍ (θ) مع المستوى، فقوانين نيوتن في هذه الحالة يمكنها أن تخبرك بإحداثيّات المقذوف في أيّ فترةٍ من الزّمن بعد الإطلاق.

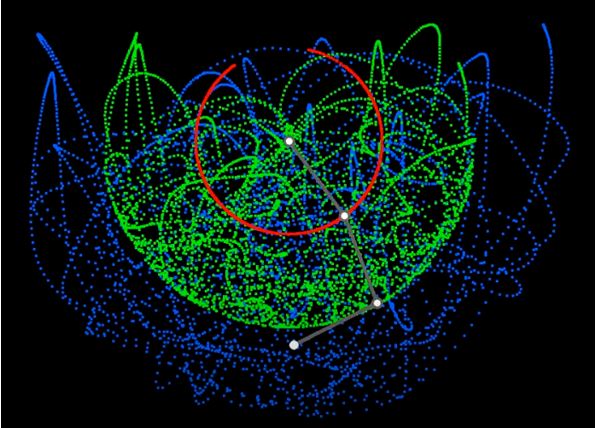
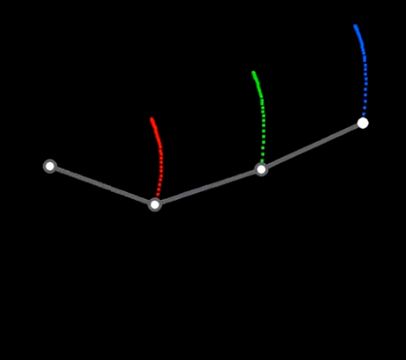
ولكن ماذا نفعل حينما نجد أنفسنا أمام نظامٍ أكثر تعقيدًا؟ فإن اعتمادنا على قوانين نيوتن في تلك الحالة سيزيد الأمور تعقيدًا. ولنأخذ على سبيل المثال نظام البندول الثّلاثيّ، في هذا النّظام بندولٌ يدور حول نقطةٍ ثابتةٍ، وبندولٌ يدور حول طرف البندول الأوّل، وبندولٌ ثالثٌ يدور حول طرف البندول الثّاني، والمطلوب هو إيجاد معادلات حركة النّظام. وتعطينا الصّورة التّالية فكرةً عن مدى تعقيد النّظام، علمًا أنّ مسار البندول الأوّل مُبيَّنٌ باللّون الأحمر، والثّاني بالأخضر، والثّالث بالأزرق.
والنّاظر إلى هذا النّظام قد يرى أنّه يصعب وصفه بالمعادلات، لكنّ إسهام أحد العلماء جعل الأمر أكثر سهولةً.

قوانين لاجرانج

أتى إلينا العالم الفرنسيّ الإيطاليّ جوزيف-لويس لاجرانج (بالفرنسيّة: Joseph-Louis Lagrange) في أواخر القرن الثّامن عشر، بإسهاماتٍ عدّةٍ في الفيزياء والرياضيّات. وهو من الرّوّاد الأوائل في علم حساب المتغيّرات (بالإنجليزيّة: Calculus of Variations) ومن روّاد الميكانيكا الكلاسيكيّة أيضًا.

وجد لاجرانج أنّ سبب قصور قوانين نيوتن يعود إلى نقطتين:

• أوّلًا نظام الإحداثيّات المستخدم،
• وثانيًا الاعتماد على المتّجهات (بالإنجليزيّة: vectors) في الحصول على النّتائج.

ومن هنا بُنيت قوانين لاجرانج على ثلاثة عناصر بديلةٍ، لتصبح لدينا قوانين قابلةٌ للاستخدام بسهولةٍ مع تلك الأنظمة الأكثر تعقيدًا.

مبدأ الفعل الأدنى (بالإنجليزيّة: The principle of least action)

استنبط عالم الرياضيّات الشّهير فيرما (بالفرنسيّة: Fermat)، نتيجةً لملاحظته لمسار الضّوء، مبدءًا ينصّ على أنّ الأجسام في الطّبيعة تسلك أقصر الطّرق. ذلك الاستنتاج كان نتيجةً لملاحظته الثّاقبة لانتقال الضّوء بين نقطتين في أقصر الطّرق وأسرعها، بالنّسبة للزّمن. وسُمّي ذلك المبدأ بمبدأ أقصر الأوقات (بالإنجليزيّة: the principle of least time). ولكن عن طريق العالم لويس موبيرتوي (بالفرنسيّة: Louis Maupertuis) وجدنا أنّ الأمور ليست بتلك البساطة. وأنّه «عندما يحدث تغيّرٌ ما في الطّبيعة، فإنّ كمّيّة الفعل المستخدمة تكون أقلّ ما يمكن»، ومن هنا نصل لمبدأ الفعل الأدنى.

يعتمد هذا المبدأ على أنّ الأجسام في الطّبيعة تميل إلى اتّخاذ المسار الّذي تبذل فيه أقلّ شغلٍ أو طاقةٍ، وذلك خلال فترةٍ زمنيّةٍ لحظيّةٍ، على أن تكون الحركة مستمرّةً (بالإنجليزيّة: continuous)، وفي ذلك  يستخدم المبدأ كميّاتٍ قياسيّةٍ (بالإنجليزيّة: scalar)، بدلًا من المتّجهات. فلتعيين حركة الجسم، نستخدم كميّات الطّاقة المبذولة بدلًا من القوى الخارجيّة المؤثّرة كما في قوانين نيوتن. فعلى سبيل المثال، لتعيين حركة جسمٍ مقذوفٍ، نحسب طاقة الحركة (T) ونطرح منها طاقة الوضع (U) الخاصّة بالجسم عند نقاط المسار المختلفة للحصول على قيم (L).

L=T-U

تعبّر قيمة (L) عن أقلّ قيمةٍ للفرق، وتلك القيمة تمثّل القيمة الفعليّة لحركة الجسم عند نقطة، أُطلق على تلك القيمة فيما بعد اسم لاجرانج (Lagrangian). ونحصل على قيمة الحركة الكليّة من تكامل قيم (L).

الإحداثيّات المعمَّمة (بالإنجليزيّة: Generalized Coordinates)

كما هو معلومٌ، فإنّ نظم الإحداثيّات لدينا كثيرةٌ، فهناك النّظام الكارتيزيّ، والقطبيّ، والاسطوانيّ، والكرويّ. ومن المعلوم لدينا أيضًا أنّ حلّ إحدى المسائل باستخدام نظامٍ ما، قد يكون أسهل من استخدام باقي الأنظمة الأخرى. ولنأخذ مثلًا النّظام الكارتيزيّ لوصف موضع نقطةٍ معيّنةٍ في الفراغ، فموضع النّقطة يعتمد على ثلاثة متغيّراتٍ (x, y, z). أمّا عن الإحداثيّات المعمّمة فلا بدّ أن تحقّق شرطين لكي تُوصف بأنّها معمّمةٌ:

• الأوّل أن تكون مستقلّة، ومعنى ذلك أنّه إذا علمنا قيمة إحدى المتغيّرات المعمّمة؛ فباقي المتغيّرات المعمّمة يمكن أن يكون لها أيّ قيمةٍ.
• الثّانية أن تكون الإحداثيّات أقلّ ما يمكن لحلّ المسألة الواحدة حيث أنّ عدد الإحداثيّات المعمّمة هو أقلّ عدد إحداثيّاتٍ يمكنه وصف المعادلة. [1]

يمكن توضيح ماهيّة تلك الإحداثيّات بالمثال التّالي، فلنفترض أنّنا نريد وصف موضع نقطةٍ على سطح كرةٍ، أيّ الإحداثيّات تكون إحداثيّاتٍ معمّمة؟ هل هي الإحداثيّات الكارتيزيّة؟ والإجابة بالطّبع لا، لأنّه إذا حدّدنا قيمة الإحداثيّ (x) والإحداثيّ (y) فهناك قيمةٌ واحدةٌ فقط يمكن أن يأخذها الإحداثيّ (z) وهي الّتي تحقّق المعادلة:

x²+y²+z² =r²

حيث (r) هو طول نصف القطر. لكن يمكننا أن نصف موضع النّقطة بشكلٍ كاملٍ من خلال متغيّرين، الأوّل هو زاوية السّمت والثاني هو زاوية الارتفاع. والملحوظة الأولى أنّ 2 هو أقلّ عددٍ من المتغيّرات يمكنه وصف موضع نقطةٍ على سطح دائرةٍ، والملحوظة الثّانية أنّنا إن حدّدنا قيمةً محدّدةً لزاوية السّمت، نرى أنّ زاوية الارتفاع يمكنها رغم هذا التّحديد أن تأخذ أيّ قيمةٍ ممكنةٍ. ولهذا تعتبر زاوية السّمت (φ) وزاوية الارتفاع (θ)، الإحداثيّات المعمّمة لهذه المسألة. وهذا المثال يوضّح لنا أنّ هذه الإحداثيّات تكون قياسيّةً. كما يجب أن نشير إلى أنّ ما يميّز الإحداثيّات المعمّمة أنّه في الحالة العامّة يمكن الاعتماد على قيم الإحداثيّات المعمّمة للحصول على قيمٍ للإحداثيّات الأخرى. فالإحداثيّ (x) في المثال السّابق يعتمد على كلٍّ من (θ) و (φ)، والإحداثيّات المعمّمة يُرمز لها على سبيل التّعميم بالرّمز (q_i) حيث أنّ (i) يمكنها أن تأخذ القيم 1 أو 2 أو 3… إلخ. فمثلًا في المثال السابق يكون (q₁=φ) و (q₂=θ).

كما أنّ السّرعة المعمّمة (بالإنجليزيّة: Generalized Velocity) ما هي إلّا مشتقّة الإحداثيّات المعمّمة بالنّسبة للزّمن ويرمز لها بالرّمز (q’_i).

القيود ودرجات الحريّة (بالإنجليزيّة: Constrains and Degrees of freedom)

لكلّ نظامٍ فيزيائيٍّ عددٌ محدّدٌ من درجات الحرّيّة، وهو نفسه عدد أقلّ إحداثيّاتٍ مستقلّةٍ يمكنها وصف موضع كلّ جزءٍ من النّظام الفيزيائيّ. ولنصف موضع جسمٍ في الفراغ، علينا أن نحدّد قيمة الإحداثيّات الثلّاثة له (x, y, z). ولعددٍ كبيرٍ (N) من الأجسام نحتاج (3N) من الإحداثيّات لوصف موضع كلٍّ منهم. لكن هل دائمًا علينا الالتزام بهذا العدد من درجات الحريّة؟ الإجابة هي لا. ففي بعض الأحيان يمكننا وضع قيودٍ على وصف النّظام؛ مثلًا أن نصف حركة جسمٍ على طاولةٍ، في هذه الحالة وضعنا قيدًا على قيمة (z)، وهو أنّ (z=c) حيث (c) هي قيمةٌ ثابتةٌ تساوي ارتفاع سطح الطّاولة. والقيد هو علاقةٌ بين الإحداثيّات. ففي حالة الكرة يمكننا كتابة القيد على الصّورة (0= x²+y²+z^{2 _} r²). وبشكلٍ عامٍّ فإنّ عدد درجات الحريّة لنظامٍ يحتوي على (N) جسمٍ يساوي (3N-K) حيث (K) يساوي مجموع القيود لكلّ جسمٍ. ففي حالة الجسم الّذي يتحرّك على الطّاولة يكون عدد درجات الحريّة: (3×1 – 1 = 2). [1]

لاجرانج ومعادلات الحركة

لقد قام العالم لاجرانج بتغيير الطّريقة الّتي ننظر بها إلى النّظام الفيزيائيّ لكي نصل إلى معادلات الحركة الخاصّة به. فبدلًا من تحليل القوى واستخدام قانون نيوتن الثّاني، تعتمد معادلات لاجرانج على قيمةٍ مستوحاةٍ من اسمه وهي لاجرانج. وأمّا عن معادلات الحركة فهي على الصّورة:

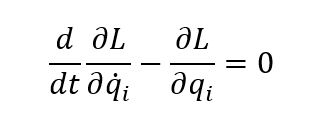
ونرى في المعادلة، الاشتقاق الجزئيّ للاجرانج، مرّةً بالنّسبة إلى الإحداثيّات المعمّمة ومرّةً بالنّسبة إلى السّرعة المعمّمة. ونلاحظ أنّ عدد المعادلات الّتي يمكنها وصف النّظام تساوي عدد درجات الحريّة. ولنأخذ معًا مثال البندول الثّلاثيّ ونطبّق عليه قانون لاجرانج. في حالة البندول الثّلاثيّ فإنّه يمكن وصف النّظام بشكلٍ كاملٍ بثلاثة متغيّراتٍ فقط، وهم الزّوايا الّتي يصنعها كلّ بندولٍ مع العموديّ: (θ₁) و (θ₂) و (θ₃)_. والخطوة الأولى لإيجاد معادلات الحركة الثّلاث هو إيجاد قيمة كلٍّ من طاقة الوضع والحركة للنّظام، ومنه نوجد قيمة اللّاجرانج. ومن ثَمّ نكتب المعادلات الثّلاثة على الصّور:

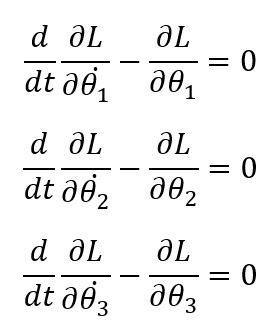
وتبسيط مثل تلك المعادلات لن يتطلّب من طالبٍ في المرحلة الجامعيّة الكثير من الوقت، ليعطينا في النّهاية 3 معادلاتٍ تفاضليّةٍ من الرّتبة الثّانية. وبشكلٍ عامٍّ فإنّ طريقة لاجرانج لنظامٍ له (N) درجة حريّةٍ تعطينا (N) معادلةٍ تفاضليّةٍ من الرّتبة الثّانية تصف النّظام. [1]

لكنّ النّظام الفيزيائيّ الموصوف بهذه الطّريقة كان في نظر العالم وليم هاميلتون (بالإنجليزيّة: William Hamilton) يحتاج إلى تعديلٍ، لتصبح طريقته قابلةً للتّطبيق في مجالاتٍ أوسع. فبالتّعديلات الّتي أضافها هاميلتون، أصبح بالإمكان أن تستخدم تلك الطّريقة بشكلٍ مباشرٍ في ميكانيكا الكمّ والميكانيكا الإحصائيّة وفروعٍ أخرى من الفيزياء. والطّريقة باختصارٍ؛ أنّه استعاض عن اللّاجرانج (L) بدالّةٍ أخرى تعرف باسمه: هاميلتون، ويُرمز لها بالرّمز (H). والفارق الجوهريّ بين الدّالتين، أنّ الدّالّة (H) لا تعتمد على السّرعة المعمّمة، كما الحال في اللّاجرانج، إنّما تعتمد على ما يسمّى بالعزم المعمّم (بالإنجليزيّة: Generalized Momentum) حيث أنّ العزم المعمّم (ρ_i) يعرف أنّه المشتقّ الجزئيّ للدّالة (L) بالنّسبة للسّرعة المعمّمة. أما عن ماهيّة الهاميلتون، فهو في معظم الحالات يساوي مجموع الطّاقة الحركيّة وطاقة الوضع (الطّاقة الكليّة). وعلى عكس لاجرانج، فإنّ لكلّ درجة حريّةٍ في النّظام، لا بدّ من كتابة معادلتين تفاضليّتين لوصف النّظام، ممّا يجعل الأمر في كثيرٍ من الأحيان أكثر قابليّةً للحلّ.

القصّة لم تنته عند هذا الحدّ، فللعالمين المذكورين في هذا المقال أعمالٌ كثيرةٌ، وميكانيكا لاجرانج وهاميلتون تحتاج إلى كتبٍ لوصف إنجازاتها ونتائجها، لكنّنا عرضنا سريعًا كيف أنّ هذين النّظامين يمكنهما ببراعةٍ حلّ أعقد المشكلات: مثل البندولات المتعدّدة، والبندول المثبّت على جرّارٍ. كما يمكن لهذين النّظامين أيضًا حلّ الأنظمة البسيطة مثل المقذوف، إلا أنّ استخدام معادلات نيوتن سيكون أكثر منطقيّةً في هذه الحالة.