تُعتبر معادلة أويلر أحد أجمل الصيغ الرياضية إن لم تكن أجملها على الإطلاق ، إلى الحد الذي سماها بعض علماء الرياضيات بالمعادلة الإلهية. فهي تحتوي على أشهر خمسة ثوابت رياضية وهي :
الواحد الصحيح (1)
الصفر (0) .
عدد أويلر (e) .
العدد التخيلي ( i ).
وأيضًا تمثل عمليتين رياضيتين أساسيتين وهما
الجمع (+) .
الضرب (ₓ) .
والغرض الأساسي من استعراض معادلة أويلر واستنتاجها ،لتوضيح الطرق المختلفة لتمثيل الأعداد العقدية ،سواءا كان :
1- تمثيل جبريا .
2- تمثيل مثلثيا أو قطبيا .
3- تمثيل أُسِّيا (تمثيل اويلر) .
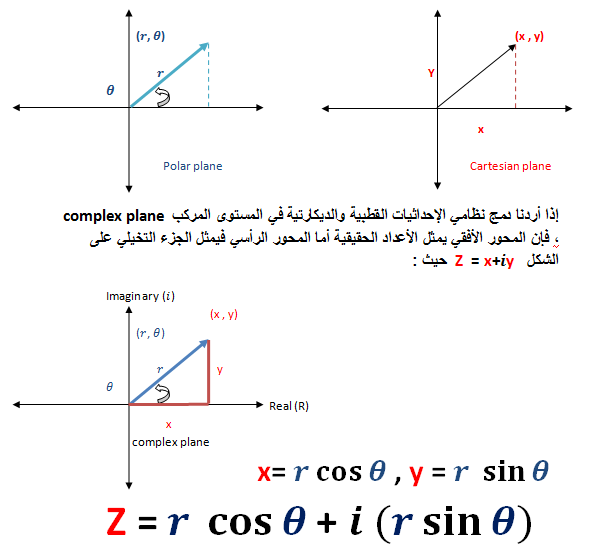
بدايةً سنبدأ بتوضيح مفهوم موقع نقطة ما في مستوى ثنائي الأبعاد.
لأي نقطة في مستوى ثنائي الأبعاد يمكن تمثيلها بنظامين من الإحداثيات :
- نظام الإحداثيات الديكارتية Cartesian coordinates
- نظام الإحداثيات القطبية Polar coordinates

إعداد :Ahmed Hosiny
مراجعة: Mohamed Sayed Elgohary
تصميم : Ayman Samy
#الباحثون_المصريون