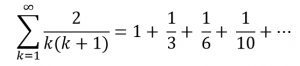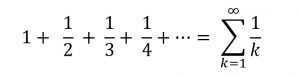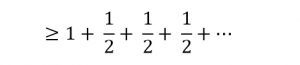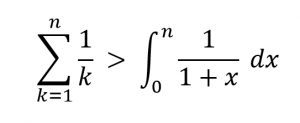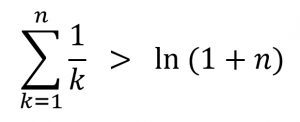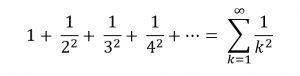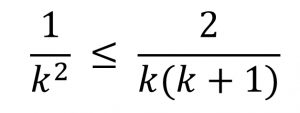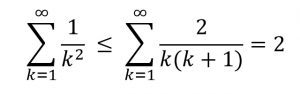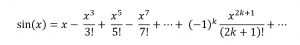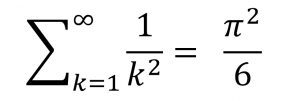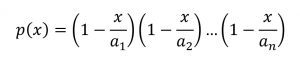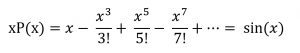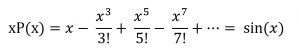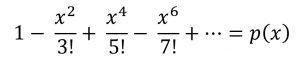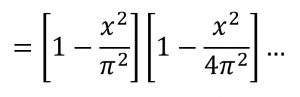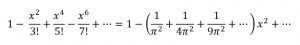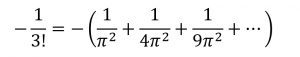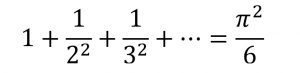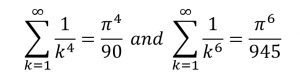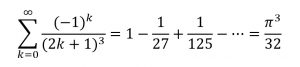يسمى المجموع اللانهائي على الصورة ![]() بالمتسلسلة اللانهائية، تظهر هذه المتسلسلات بكثرة في الرياضيات الحديثة، والكثير حول هذا الموضوع تم تطويره أثناء القرن السابع عشر. وقد أكمل «ليونهارد أويلر – Leonhard Euler» دراسة المتسلسلات اللانهائية واستطاع أن يقوم بحل مسائل هامة.
بالمتسلسلة اللانهائية، تظهر هذه المتسلسلات بكثرة في الرياضيات الحديثة، والكثير حول هذا الموضوع تم تطويره أثناء القرن السابع عشر. وقد أكمل «ليونهارد أويلر – Leonhard Euler» دراسة المتسلسلات اللانهائية واستطاع أن يقوم بحل مسائل هامة.
واحدة من أهم المتسلسلات هي المتتابعة الهندسية a + ar + ar2 + …… + arn أساس هذه المتتابعة هو ![]() ، وحل هذه المتتابعة
، وحل هذه المتتابعة ![]() ، ومن هنا يمكن بسهولة استنتاج أن
، ومن هنا يمكن بسهولة استنتاج أن ![]()
كانت هذه واحدة من أوائل النتائج العامة التي عُرفت أثناء القرن السابع عشر. ومن المتتابعات التي عرفت أيضًا
فإذا اعتبرنا 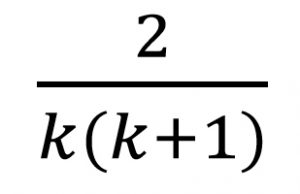 هو الحد العام k, فإن الحد k+1 هو
هو الحد العام k, فإن الحد k+1 هو ![]() ، وباستخدام اختبار النسبة
، وباستخدام اختبار النسبة ![]() ينتج أن
ينتج أن ![]() ، وبالقسمة على k2 بسطًا ومقامًا وأخد النهاية ينتج 1 أي يفشل الاختبار. فإذا قمنا بالحل على طريقة رابي
، وبالقسمة على k2 بسطًا ومقامًا وأخد النهاية ينتج 1 أي يفشل الاختبار. فإذا قمنا بالحل على طريقة رابي ![]() ، وبتوحيد المقام داخل القوس ثم ضرب البسط في k ثم قسمة كلًا من البسط والمقام على k2 وأخد النهاية تكون النتيجة 2، أي أن هذه المتسلسلة تقاربية. قد يخدعنا ذلك بأنه يمكن استبدال مجموع لانهائي من الحدود بعدد محدد ولكن هذا ليس حقيقيًا بالنسبة للمتسلسلة الشهيرة المعروفة بـ «المتسلسلة المتناسقة – Harmonic Series»
، وبتوحيد المقام داخل القوس ثم ضرب البسط في k ثم قسمة كلًا من البسط والمقام على k2 وأخد النهاية تكون النتيجة 2، أي أن هذه المتسلسلة تقاربية. قد يخدعنا ذلك بأنه يمكن استبدال مجموع لانهائي من الحدود بعدد محدد ولكن هذا ليس حقيقيًا بالنسبة للمتسلسلة الشهيرة المعروفة بـ «المتسلسلة المتناسقة – Harmonic Series»
اكتشاف أن هذه المتسلسلة تتباعد يرجع إلى الفرنسي «نيكول اورسمي – Orseme»، حيث قام بصياغة الإثبات التالي حوالي عام 1350
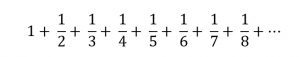
حيث قام بخلق متسلسلة أخرى بحيث يكون كل حد فيها يساوي أو أقل من الحد المناظر له في المتسلسلة الأصلية، بحيث يكون كل حد مساوي لل ![]() مرفوع لأكبر أس، وباستخدام اختبار المقارنة إذا استطعنا أن نثبت أن المتسلسلة الصغرى (المخلقة) تباعدية إذًا بالضرورة أن المتسلسلة الأصلية تباعدية أيضًا.
مرفوع لأكبر أس، وباستخدام اختبار المقارنة إذا استطعنا أن نثبت أن المتسلسلة الصغرى (المخلقة) تباعدية إذًا بالضرورة أن المتسلسلة الأصلية تباعدية أيضًا.
لكن في الحقيقة هذه المتسلسلة تتباعد بشكل إلى حدٍ ما بطيء، ولحساب سرعة التباعد بدقة نستخدم إثبات حديث عن طريق اختبار التكامل، والذي يعتمد على مقارنة الشكل البياني للدالة بحدود المتسلسلة، وعن طريق تكامل الدالة نستطيع المقارنة مع حدود المتسلسلة.
في حالتنا هذه نقارن حدود المتسلسلة بالمساحة تحت التمثيل البياني للدالة ![]()
ولكن هذه الدالة ![]() غير محدودة ولذا نستطيع جعل
غير محدودة ولذا نستطيع جعل ![]() ممتدة بالحد الذي نريده.
ممتدة بالحد الذي نريده.
يمكن تعريف المتسلسلة الهارمونية بأنها «مجموع مقلوبات الأعداد الطبيعية»، المتسلسلة الشبيهة لها هي «مجموع مربعات مقلوبات الأعداد الطبيعية»
ولنبدأ في طرح بعض الأسئلة أولًا هل هذه المتسلسلة تقاربية؟ وإذا كانت كذلك ترى ما هو المجموع؟ ولكن في البداية نلاحظ أن![]()
ومن هنا يمكن أن نستنتج بسهولة أن
وبالمقارنة مع المتسلسلة الأولى التي قمنا بحلها يمكن أيضًا استنتاج أن
المتسلسلة تتقارب لكن إيجاد القيمة العددية للمجموع كان صعبًا للغاية؛ حتى أن برنولي فشل في إيجاد القيمة وكذلك منجولي وليبينز. ومن ثم أصبح إيجاد المجموع معروف بـ«معضلة بازل – Basel problem» والآن سنناقش كيف استطاع أويلر حل هذه المعضلة.
ولكن قبل حل هذه المعضلة سنتطرق إلى النظرية التي استخدمها أويلر والتي مكنته من كتابة الدالة ![]() على طريقة «المفكوك – infinite polynomial»
على طريقة «المفكوك – infinite polynomial»
وتسمى هذه بمتسلسلة القوى للدالة ![]() ، حيث أن حدودها x مرفوعة للقوى. ومن الممكن تقريب الدالة
، حيث أن حدودها x مرفوعة للقوى. ومن الممكن تقريب الدالة ![]() إذا كانت x صغيرة. وباستخدام الحدود الأولى من المتسلسلة من الممكن التقريب
إذا كانت x صغيرة. وباستخدام الحدود الأولى من المتسلسلة من الممكن التقريب![]()
توصل أويلر عام 1735 إلى النتيجة التالية
الحقيقة أن هذه النتيجة مميزة ولكنها صادمة أيضًا. لم يتوقع أحد ظهور القيمة ![]() – وهي النسبة بين محيط الدائرة إلى قطرها – كناتج جمع. بدأ أويلر مع مفكوك
– وهي النسبة بين محيط الدائرة إلى قطرها – كناتج جمع. بدأ أويلر مع مفكوك ![]() من الدرجة n مع وضع بعض الخصائص:
من الدرجة n مع وضع بعض الخصائص:
ثم قدم السيد أويلر ادعاءً أن ‹‹ما يجري على المفكوكات النهائية يجري على المفكوكات اللانهائية›› وبتطبيق هذا الادعاء
الناتج صفر عندما ![]() لكل k=1,2,… حيث تكون قيمة sin(x) مساوية للصفر. والآن نستطيع أن نستخدم الادعاء
لكل k=1,2,… حيث تكون قيمة sin(x) مساوية للصفر. والآن نستطيع أن نستخدم الادعاء
كان أويلر جريئًا في ادعاءه حيث أننا حصلنا في النهاية في حالتنا هذه على إجابة صحيحة، والخدعة التي قام بها أويلر هي كتابة P(x) بطريقتين مختلفتين حيث يقوم باستغلال ذلك من خلال الطرف الأيمن، وعلى الرغم من حاصل الضرب اللانهائي سيصير معقدًا إلا أننا نضمن وجود الحد الثابت 1 ونستطيع تجميع معاملات x2 أيضًا بدون عناء
ومن مقارنة معاملات x2 نجد أن
وبأخذ ![]() عامل مشترك وضرب وسطين طرفين نستنتج بسهولة أن
عامل مشترك وضرب وسطين طرفين نستنتج بسهولة أن
لكن أويلر لم يتوقف عند هذا الحد بل استطاع أيضًا بنفس الطريقة استنتاج أن
وباستخدام هذه الطريقة نستطيع إيجاد 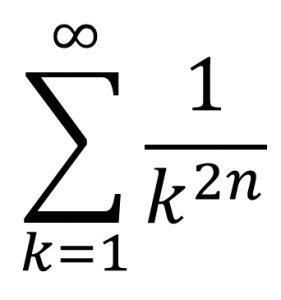
ولكن ماذا إذا كان الأس عددًا فرديًا؟
الإجابة: أننا لا زلنا لا نعرف. لكن تظل هذه معضلة مفتوحة نبحث لها عن حل، بالطبع حاول أويلر إيجاد حل لكنه فشل. ومع ذلك تمكن من حل هذه الواحدة
إعداد: Marwa Sleem
مراجعة وتصميم: Mohamed Qamar-Edddine
المصدر: https://goo.gl/wY1iXz
#الباحثون_المصريون