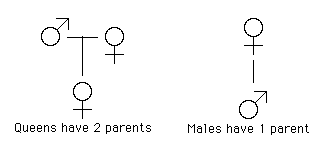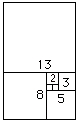متسلسلة فيبوناتشي والنسبة الذهبية
الجزء الثاني: الحيوانات
التكاثر عند الأرانب
كانت المشكلة الأصلية التي حاول فيبوناتشي التحقق منها في العام 1202 م هي كيفية تكاثر الأرانب بسرعة في ظروفٍ مثالية. وقد قام بتجربةٍ خيالية غير واقعية على زوجٍ من الأرانب؛ ذكر وأنثى.
لنفترض أن الزوج المولود حديثًا من الأرانب وهو عبارة عن ذكرٍ واحد، وأنثى واحدة، ووُضِعَا في حقل. ستكون هذه الأرانب قادرةً على التزاوج في عمر شهرٍ واحد، وفي نهاية الشهر الثاني ستنجب الأنثى زوجًا آخر من الأرانب. وبافتراض أن الأرانب التي لدينا لا تموت أبدًا، وأن الأنثى تُنجب دائمًا زوجًا واحدًا جديدًا؛ ذكر واحد، وأنثى واحدة. كان هذا اللغز الذي قدمه فيبوناتشي.
كم سيكون عدد أزواج الأرانب في سنةٍ واحدة؟
في نهاية الشهر الأول، تتزاوج، ولكن لا يزال هناك زوج واحد فقط في الحقل.
في نهاية الشهر الثاني تنجب الأنثى زوجًا جديدًا، وحتى الآن هناك زوجان من الأرانب في الحقل.
في نهاية الشهر الثالث، الأنثى الأصلية تنتج الزوج الثاني، وبالتالي يكون لدينا 3 أزواج في الحقل.
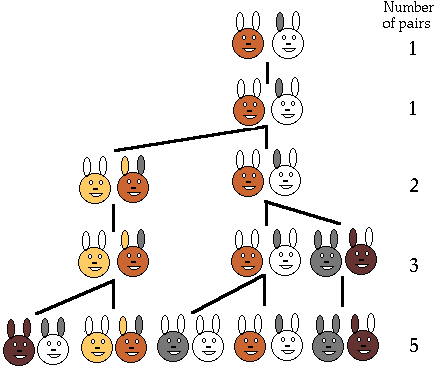
في نهاية الشهر الرابع، تكون قد أنجبت الأنثى الأصلية زوجًا جديدًا آخر، والأنثى التي وُلِدَت قبل شهرين تُنتج أول زوجٍ لها أيضًا، وبالتالي يكون لدينا في الحقل 5 أزواجٍ من الأرانب. كما هو مُوضَّح بالشكل التالي:
عدد أزواج الأرانب في الحقل في بداية كل شهر سيتبع متسلسلة فيبوناتشي 1، 1، 2، 3، 5، 8، 13، 21، 34، …
وإذا افترضنا أن (F(n تعني «عدد من الأزواج من الأرانب في الحقل في بداية الشهر n»، وبالتالي فإن
F(n) = F(n-1) + F(n-2) , F (2) = 1 , F (1) = 1
وهو بالضبط تعريف أرقام فيبوناتشي
أولًا: نبدأ الشهر الأول مع زوجٍ واحدٍ وهو المولود حديثًا، لذا فإن: F (1) = 1
خلال الشهر الثاني هناك أيضًا زوج واحد فقط؛ لأنها لم تنمو بما فيه الكفاية حتى الآن لتنجب، لذا فإن: F (2) = 1
وبما أننا نفترض أنها تتزاوج في سن شهرين ثم تنجب زوجًا جديدًا في بداية الشهر 3. لذلك، وبعد الشهر الثاني، كم سيكون عدد الأرانب؟ أي ما هو (F(n؟
جميع الأرانب مقارنةً بالشهر الذي سبقه سيكون هناك (F(n-1 منهم على قيد الحياة، لذلك هناك ما لا يقل عن (F(n-1 منهم. أي زوج من الأرنب يكون على قيد الحياة بعد شهرين من الآن قادر على إنتاج زوجٍ جديد، ونحن نفترض أنها سوف تنجب دائمًا زوجًا واحدًا جديدًا شهريًا. وهكذا فإن عدد الأزواج المولود حديثًا هو نفس عدد الأزواج بعد شهرين: (F(n-2. وبالتالي فإن كل الأرانب التي على قيد الحياة من الشهر الماضي أو المولودة حديثًا هذا الشهر، تكون كالتالي:
(F(n) = F(n-1) + F(n-2 إذا كان: n > 2 وهي مجرد تعريف أرقام فيبوناتشي بدءًا من 0 , 1.
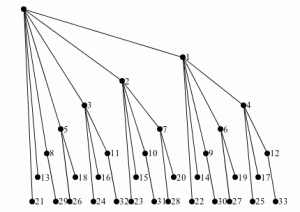
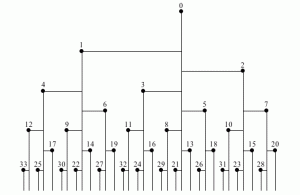
الرسومات السابقة تُمثِّل نفس المعلومات. وقد تم ترقيم الأرانب للتمكن من مقارنتها وعدها، على النحو التالي:
جميع الأرانب التي وُلِدَت في نفس الشهر هي من نفس الجيل وموجودة في نفس المستوى في الشجرة.
وقد تم ترقيم الأرانب ترقيمًا مميزًا، حتى أنه في نفس الجيل يتم ترقيم الأرانب الجديدة في ترتيب رقم آبائهم. وبالتالي 5 و6 و7 هم الأطفال من 0 و1 و2 على التوالي.
الأرانب المصنفة بأنها تحمل رقم فيبوناتشي هي من الأرانب الأصلية (0) في أعلى الشجرة.
مشكلة الأرانب هذه ليست واقعية جدًا، كما قلنا حيث كما يبدو أن الذكور والإناث من نفس الأباء تتزاوج معًا، وهذا وراثيًا يؤدي إلى مشاكل. يُمكننا تجنب هذا بأن الأنثى من أي زوج تتزاوج مع أي ذكر وتنتج زوجًا آخر. وهناك مشكلةٌ أخرى وهي لا تحدث في الحياة الواقعية، وهي أن كل ولادة هي بالضبط اثنان من الأرانب، ذكر واحد وأنثى واحدة.
التكاثر عند الأبقار
أبقار هنري دودني (Dudeney’s cows)
صاحب الألغاز الإنجليزي هنري دودني 1857- 1930 كتب العديد من الكتب الممتازة عن الألغاز. في واحد من الألغاز استبدل أرانب فيبوناتشي بالأبقار، مما يجعل المشكلة أكثر واقعية عمَّا لاحظناه سابقًا. وقال أنه تجنب المشاكل عن طريق الملاحظة الحقيقية، والاهتمام فقط بعدد الإناث.
وقد استبدل الشهر بالسنة، والأرانب بالثيران «الذكور»، والأبقار «الإناث»، في مشكلةٍ برقم 175 في كتابه «536 لغزٍ ومشكلةٍ غريبة – 536 puzzles and Curious Problems»
تُنتج البقرة العجل الأول لها في سن العامين، وبعد ذلك تنجب عجلًا واحدًا آخر كل عام، وبالتالي فإن عدد العجول يتبع متتالية فيبوناتشي، على افتراض أنها لا تموت
وأوضح كيف تتكاثر الأبقار باستخدام متتالية فيبوناتشي.
مثلًا: 1 سنة = 1 بقرة
سنتان = 1 بقرة
3 سنوات = 2 من الأبقار
4 سنوات = 3 من الأبقار
5 سنوات = 5 من الأبقار
6 سنوات = 8 من الأبقار
هذا هو تبسيط أفضل لمشكلة واقعية تماما الآن.
لذلك دعونا ننظر إلى حالةٍ أخرى من واقع الحياة والتي تُمثِّل تمامًا متسلسلة فيبوناتشي، وهي نحل العسل.
نحل العسل وشجرة العائلة
هناك أكثر من 30000 نوعٍ من النحل. واحد من هذه الأنواع يعرفه معظمنا جيدًا وهو نحل العسل، يعيش في مستعمرةٍ تُسمَّى خلية، ولديهم شجرة عائلة غير عادية. في الواقع، هناك العديد من الميزات غير العادية عن نحل العسل، وفي هذا القسم سوف نُظهر كيف تَحسِب أرقام فيبوناتشي أسلاف (آباء وأجداد) النحل.
بعض الحقائق غير العادية حول نحل العسل مثل:
ـ ليست لدى كل نحلة اثنين من الآباء؛ أب وأم!
ـ في مستعمرة نحل العسل هناك واحدة مميزة من الإناث تُسمَّى الملكة.
ـ هناك العديد من النحل العامل من الإناث أيضًا ولكن بخلاف الملكة؛ لأن النحلة العاملة لا تُنتج البيض.
ـ هناك بعض النحل لا يعمل، وهو من الذكور.
ـ يتم إنتاج الذكور من البيض غير المُخصَّب للملكة، لذلك ذكور النحل ليس لها أب ولكن أم فقط!
ـ جميع الإناث تُنتَج عندما تتزاوج الملكة مع الذكر، ويكون لها أبوين. وعادةً ما ينتهي بها المطاف كعاملات، ولكن يتم تغذية بعضها بمادةٍ خاصة تُسمَّى «غذاء ملكات النحل» مما يجعلها تنمو لتكون ملكاتٍ مُعدَّة لبدء مستعمرةٍ جديدة عندما يُشكِّل النحل سربًا ويترك الخلية بحثًا عن مكانٍ لبناء خلية جديدة.
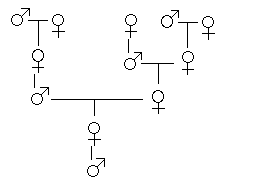
دعونا ننظر إلى شجرة عائلة النحل الذكور.
لديه أم واحدة أنثى.
لديه 2 من الأجداد، حيث أن والدته من أبوين، ذكر وأنثى.
لديه 3 من آباء الأجداد، جدته من أبوين ولكن جده واحد فقط… وهكذا.
والجدول التالي يُوضِّح عدد الآباء والأجداد لكلٍّ من النحلة الأنثى والذكر:
عدد الأباء |
عدد الأجداد |
عدد آباء الأجداد |
عدد أجداد الأجداد |
عدد آباء أجداد الأجداد |
|
ذكور النحل |
1 |
2 |
3 |
5 |
8 |
إناث النحل |
2 |
3 |
5 |
8 |
13 |
الحلزون الذهبي
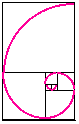
يَظهَر الشكل الحلزوني في العديد من الكائنات الحية وفي الطبيعة من حولنا كما في الأصداف البحرية. ويمكننا رسم الحلزون عن طريق رسم مربعين متجاورين، مساحة كلٍّ منهما 1، ثم نرسم مربعًا آخر مجاور لهما مساحته 2، ثم نرسم مربعًا مجاور لهما مساحته 3، ثم نرسم مربعًا آخر مجاور لهما مساحته 5، ثم نرسم مربعًا آخر مساحته 8… وهكذا، وينتج مستطيل تكون النسبة بين طوله وعرضه هي النسبة الذهبية، ثم بعد ذلك نرسم قوسًا بدايةً من رأس المربع الأصغر على شكل ربع دائرة في اتجاه عقارب الساعة فيكون الناتج هو الحلزون الذهبي. والصور التالية توضح ذلك:
لا يقتصر النمو في شكل حلزوني في عالم الحيوان فقط على الأصداف البحرية. ولكنه موجود في العديد من الأشياء في الطبيعة. ويمكن رؤية أمثلة من المنحنيات تستند إلى الحلزون؛ كما في أنياب الفيلة والماموث المنقرض ومخالب الأسود والحيوانات مثل الغزلان والماعز، والكباش عند نمو قرونها في أشكالٍ حلزونية تستند إلى النسبة الذهبية. نِسَب الوجه والجسم في العديد من الثدييات تتوافق مع النسبة الذهبية، وتشمل النمور والحيتان والدلافين وأسماك القرش، وطيور البطريق أيضًا تحمل النسبة الذهبية في أبعاد الجسم.
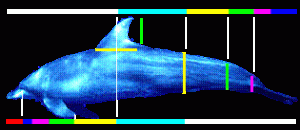
كما أن الطيور مُصمَّمة بطريقة أكثر جمالًا وأناقةً من حيث وزن الجسم، والهيكل العظمي، وطول الجناحين، وشكل وقوة المنقار، وموقع عيونهم والرؤية، وغيرها من الحواس التي تُوفِّر لهم القدرة على عمل أشياء محددة، وكذلك الأسماك تتبع النسبة الذهبية في أجزاء جسمها، والزعانف والذيل وتمثل النسبة الذهبية من أبعاد جسم الدلفين، أبعاد الزعنفة الظهرية هي نسبة ذهبية كما هو موضح في الصور، الأجزاء الصفراء والخضراء والحمراء والزرقاء، سمك ذيل الدلفين يتوافق مع المقطع الذهبي وكذلك الخط من الرأس إلى الذيل. وأسماك نجمة البحرهي الشكل الدقيق الذي يُمثِّل النسبة الذهبية. والصور تظهر هذا بوضوح.