

هو منحنى على شكل القلب، ينتج عن مسار نقطةٍ ثابتة على محيط دائرة، وهذه الدائرة تدور دون انزلاق حول دائرةٍ أخرى ثابتة لها نفس نصف القطر. وهذا الاسم مُشتق من الكلمة اليونانية (kardioedides)، وتتكون من القلب (kardia) وشكل (edides). وهذا المنحنى يشبه قطاعًا عرضيًّا من التفاحة.
أول من درس منحنى القلب هو Ole Christensen Roemer عام 1674 في محاولته للوصول إلى أفضل تصميم لأسنان التروس، ومع ذلك لم يأخذ المنحنى هذا الاسم حتى استخدمه عالم الرياضيات الإيطالي Johann Castillon في ورقة بحثية بعام 1741.
المعادلة القطبية لمنحنى القلب:
a هي نصف قطر الدائرة، θ هي الزاوية القطبية
 r = (a + a cos θ) r = (a – a cos θ)
r = (a + a cos θ) r = (a – a cos θ)
ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ
 r = (a + a sin θ) r = (a – a sin θ)
r = (a + a sin θ) r = (a – a sin θ)
والمعادلة الكارتيزية له هي:
(x2 + y2 + ax)2 = a2 (x2 + y2)
والمعادلة البارامترية هي:
x = a cos t (1 – cos t) , y = a sin t (1 – cos t )
مساحة سطح Cardioid تُعطى من العلاقة التالية:
π a2 A = 6
سنلاحظ أن مساحة منحنى القلب تساوي 6 أضعاف مساحة الدائرة التي نتج عنها هذا المنحنى.
طول القوس الناتج من هذا المنحنى يُمكن حسابه بالعلاقة التالية:
L = 16 a
حيث a نصف قطر الدائرة.
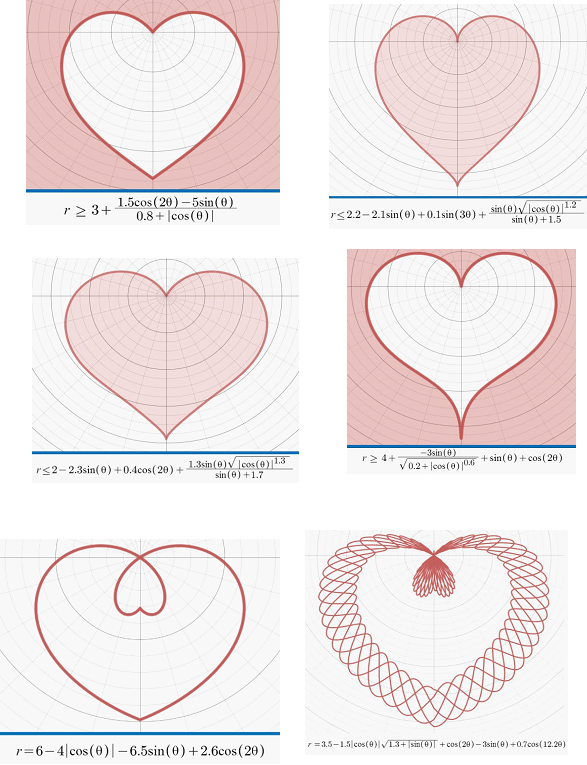 عادةً ما يتم تمثيل منحنى القلب في نظام الإحداثيات القطبية، ولكن يمكن تمثيله في نظام الإحداثيات الكارتيزية. وهذه بعض الأشكال للمنحنى القلبي ومعادلاتها كما يلي:
عادةً ما يتم تمثيل منحنى القلب في نظام الإحداثيات القطبية، ولكن يمكن تمثيله في نظام الإحداثيات الكارتيزية. وهذه بعض الأشكال للمنحنى القلبي ومعادلاتها كما يلي:
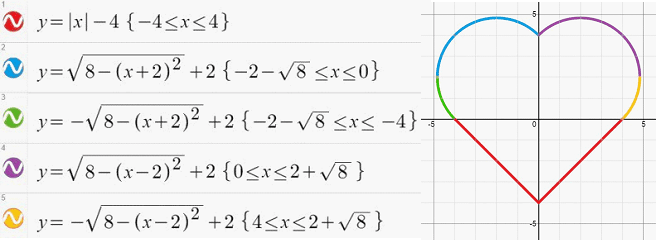 يوجد خمس معادلات إذا تم رسمها على مستوى الإحداثيات الكارتيزية معًا يتكون شكل القلب وهي كما في الشكل التالي:
يوجد خمس معادلات إذا تم رسمها على مستوى الإحداثيات الكارتيزية معًا يتكون شكل القلب وهي كما في الشكل التالي:
ترجمة وتصميم: Mahmood Yosef Mahmood
مراجعة:
Mohamed Sayed Elgohary
المصدر:

