إن أردنا أن نذكر واحدةً من أهم السِّماتِ والخصائصِ المُلفتة في الفيزياء الحديثة وعلم الكونيات فلن نجد أفضل من فكرة «اللانهائية»، تلك التي تلوح كالبدر في ليلةٍ ظلماء، فتراها تارةً في هذا الجانب، وتارةً في ذاك، حتى ليخيل إليك أنها تطوف معك حيثما اتجهت. ومن أشهر وأظهر ما يُضرب به المثل في هذا الباب، ذلك القول بوجود عددٍ لا نهائي من المجرات في هذا الكون الفسيح، أو ذاك الرأي الذي يذهب إلى أن الأكوان متعددةٌ، وأنها تتكاثر كما يتكاثر النمل، فلا يُحصى لها عدد، ولا يُدرك لها غاية، حتى لكأن كل كونٍ منها عالمٌ قائمٌ بذاته، يختلف عن غيره كما يختلف المرءُ عن توأمه.
إذا ما تأملت في قضيّة اللانهاية في عالم الجسيمات الدقيقة، لا سيما في البحث عن إكمال النظريات الفيزيائية في حقل فيزياء الجسيمات – أو ما يُعرف أحيانًا بفيزياء الطاقة العالية -، فإنك واجدٌ نفسك أمام مسألةٍ جديرة بالتفكر. ألا وهي: هل تستطيع هذه النظريات أن تبقى منسجمةً ومتناسقةً في ذاتها حين نغوص في عمق هذا العالم الدقيق وتلك المسافات التي تلامس اللانهاية في صغرها؟ ذلك أن الطرائق والأساليب الراهنة كثيرًا ما تفضي إلى اختلافات واضحة وانحرافات جليّة في الكميات الفيزيائية. وهنا يتجلى ارتباط اللانهاية بالسعي المتواصل نحو توحيد علم الفيزياء كله في نظرية واحدة أساسية، تجمع في جوهرها جميع الظواهر، سواءً كانت معروفة أو مجهولة، وعلى اختلاف المسافات، من الصغير الذي لا يُرى إلى الكبير الذي يعجز العقل عن تصوره، دونما حد أو قيد يمنع من تطبيقها. ومن ثمَّ يبرز السؤال الذي يلح على الأذهان: هل تُحتِّم هذه النظرية وجود اللانهاية الحقيقية في الطبيعة؟ أم أن اللانهاية تبقى مجرد فكرة ذهنية ومفهوم رياضي تصوري لا يتجاوز عقولنَا ولا يتعدى تصوراتنا؟
إذا تأملنا في مسألة اللانهاية من جهة الواقع العملي، نجد أنها تستحق أن يُمعن فيها النظر ويُطال فيها التفكير. ولعل كثيرًا من الفيزيائيين يُخدَعون برمز اللانهاية (∞)، فيحسبون أن ظهورها في النظريات العلمية أمرٌ مألوفٌ، لا يثير قلقًا ولا يستدعي ريبةً، وأنها جزءٌ من نظام الكون الذي نعيش فيه. لكن الحال غير ذلك؛ فاللانهاية ليست مجردَ رقمٍ كبيرٍ جدًا؛ بل هي ليست رقمًا من الأساس. إنها في حقيقتها وبطبيعتها وتعريفها أمرٌ يتعذر الوصول إليه، فلا سبيل لإدراكها مهما طال الزمان ومهما استخدمت من الوسائل والطرق. ولذا، لا يجوز أن نعتقد أن اللانهاية تتحقق فعليًا في هذا الكون المادي، لا ولا حتى في تلك الأكوان المتعددة التي يفترضها البعض. وقد أجاد ديفيد هيلبرت وأحسن قولًا حين كتب يقول:
«في حين أنّ مفهوم اللانهاية يُعدُّ أمرًا ضروريًا لأغراض رياضية مختلفة، إلا أن اللانهاية لا يمكن أن تتحقق في أيِّ مكان في الواقع الفعلي مطلقًا، بغض النظر عن التجارب التي ستقوم بها، أو الملاحظات التي ستستعين بها، أو المعرفة التي سيتم الاحتكام إليها.»
يمكننا أن نتأمل في العلاقة الثنائية التي تجمع بين الصفر – أو اللاشيء – من جهة، وبين اللانهاية من جهة أخرى، حيث يظهر هذا الارتباط جليًا في قانون الهوية الأولي في الرياضيات. فإذا قلنا إن 1 ÷ 0 = ∞، وإذا لم يتحقق أحد جانبي هذه المعادلة في الطبيعة، فلن يتحقق الجانب الآخر أيضًا. وبناءً على هذا الفهم، يمكننا القول إن الصفر ذاته لا يمكن أن يوجد فعليًا في هذا العالم المادي. فالصفر، حين نفهمه على أنه غيابٌ تامٌ لأي شيء في الزمكان، يتناقض مع ما نعرفه عن طبيعة الكون، إذ يؤكد مبدأ عدم اليقين في ميكانيكا الكم، ونتائج نظرية المجال الكمي، أن “العدم المطلق” لا يمكن أن يتحقق، وأن الفراغ ليس بالعدم بأي حال من الأحوال.
ومن هنا، نرى أن بعض الفرضيات الفيزيائية الأخيرة التي تشير إلى احتمال وجود اللانهاية فعليًا في الواقع المادي تتعارض بشكل صارخ مع رؤية هيلبرت. هذا التعارض يتفاقم عند النظر إلى بعض القضايا التي لا تزال دون حل في الفيزياء الحديثة، مثل تشعبات ونتائج نظرية المجال الكمي، وافتراض وجود المتفرِّدات «singularities» في نظرية النسبية العامة. فاللانهاية، مثلها مثل الصفر تمامًا، فكما أن الصفر غير قابل للتحقق في الواقع المادي، تظل اللانهاية بدورها مفهومًا نظريًا لا يتجاوز حدود الفكر إلى عالم الواقع.
حالة الاتساق
أشار هيلبرت إلى أنواعٍ شتى من اللانهاية، لكن إذا أردنا أن نقتصر حديثنا عن تلك اللانهايات التي تتعلق بعالم الفيزياء، فإننا نقف عند نوعين مختلفين اختلافًا جوهريًا. أما النوع الأول، فهو ذاك الذي سنرمز له بالرمز VL(∞)، وهو اللانهاية التي تُستخدم للإشارة إلى رقم أو مقدار كبير جدًا، لكنها تظل مجرد تمثيلٍ رياضيٍّ أو تعويضٍ عدديٍّ دون أن تصل إلى الحقيقة المادية. وأما النوع الثاني، الذي سنرمز له بالرمز ESS(∞)، فهو اللانهاية التي تحمل في طياتها تناقضاتٍ تتعارض مع طبيعتها، كما يتجلى ذلك في المثال المعروف بفندق هيلبرت.
ولمّا كانت الفيزياء تستند على استخدام اللانهاية في بعض مسائلها، فقد اقتصرت على النوع الأول VL(∞)، ولم تلتفت إلى النوع الثاني ESS(∞)، ذلك أن النوع الأول يخدم أغراضنا في القيام بالعمليات الحسابية الرياضية من حيث تقريب النتائج إلى درجة كبيرة جدًا، دون أن يعني ذلك أن شيئًا في الطبيعة يحمل في ذاته لانهاية فعلية. ولنا في متسلسلة فورييه «Fourier series» خير مثالٍ على ذلك، حيث يتطلب الأمر لتمثيل دقيق لدالة ترددات موجة معينة استعمال عدد لا نهائي من الحدود، ولكن هذا لا يعني بالضرورة وجود عدد لا نهائي من الترددات في النظام الفيزيائي الحقيقي. ففي حالة الوتر المهتز، نجد أن هذا الأمر مردّه إلى طبيعة المادة الذرية ونظرية الكم التي تضع لنا حدودًا لا يمكن تجاوزها.
ولا ضير في استعمال عددٍ لا نهائي من الحدود في الحسابات إذا كان الخطأ الناتج عن ذلك ضئيلًا جدًا، خاصةً إذا كان قيامنا بالتجارب قد يؤدي إلى أخطاء أكبر. ولكن السؤال الذي يفرض نفسه في الرياضيات التطبيقية هو: كم عدد الحدود التي ينبغي إضافتها للحصول على دقة كافية لوصف النظام الفيزيائي الواقعي؟ أو بصيغة أخرى: كم عدد التوافقيات التي يجب أن تُضمّن في معادلة لصنع جهاز ينتج الصوت ليُظهر لنا نغمةً أقرب ما تكون إلى آلة الكمان الحقيقية؟
حتى الآن، كانت جميع استخدامات اللانهاية في الفيزياء من النوع الأول وليس من النوع الثاني. لقد وجدَ الفيزيائيون أنه من المناسب استخدام هذا النوع من اللانهاية كمفهومٍ رياضيٍّ حيث تعتبرُ فيه اللانهايةُ شيئًا يقتربُ «limit» أو يؤولُ إلى أعدادٍ كبيرةٍ جدًّا، مع الأخذِ في الاعتبار أنَّ الواقعَ الماديَّ لا يحتوي على لانهايةٍ لأيِّ شيءٍ على الإطلاق. مثالٌ على ذلك هو متسلسلةُ فورييه «Fourier series»: فبينما يتطلبُ التمثيلُ الرياضيُّ عددًا لا نهائيًا من الحدود للحصول على تمثيل دقيق للدالة التي تمثل ترددات موجة معينة، فإن هذا لا يعني في الواقع أن هناك عددًا لا نهائيًا من الترددات الفيزيائية التي تحدثُ في النظام الفيزيائيِّ الحقيقي. في حالة الوتر المهتزِّ، يعود ذلك إلى الطبيعة الذرية للمادة ونظرية الكم. لكن لا ضرر في استخدامِ عددٍ لا نهائي من الحدود في حساباتنا إذا كان الخطأ صغيرًا جدًا، خاصةً إذا كانت نسبةُ الخطأ أقلَّ بكثيرٍ من نسبةِ الخطأِ التي تحدثُ في التجاربِ الواقعية. لكن السؤالَ المثيرَ في الرياضيات التطبيقية هو: كم عددُ الحدودِ التي يجب إضافتها وكتابتها للحصول على نتيجة دقيقة بما يكفي لوصف النظام الحقيقيِّ الواقعي؟ وكم عددُ التوافقيات التي يجبُ تضمينُها في جهاز توليف الصوت لجعلِه يبدو كآلةِ الكمان الحقيقية؟
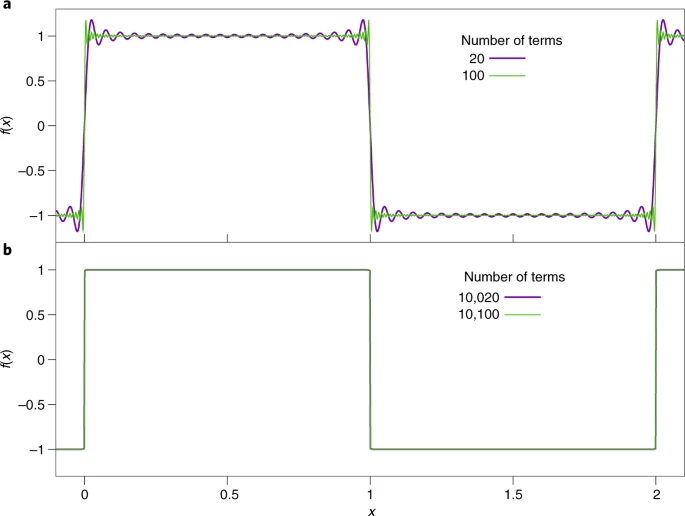
b) عندما يكون عدد الحدود كبيرًا بما يكفي لإعادة إنتاج الوظيفة الحقيقية بدقة أعلى مما يمكن اكتشافه تجريبيًا، فإن إضافة المزيد من الحدود لن يغير النتيجة بطريقة يمكن قياسها.
في معظم الحالات، يتم استخدام اللانهاية VL(∞) كرمز يُمَثل عددًا كبير جدًا، وبطريقة تجعل ممارستنا الفيزيائية لا تعتمد بشكل كبير على القيمة الفعلية لهذا الرقم الكبير، بشرط أن تكون القيمة الفعلية كبيرة جدًا بما يكفي حاجاتنا الفيزيائية التجريبية. على النقيض من ذلك، فإن الطبيعة المتناقضة للانهاية الواقعية ESS(∞) تتمثل في العلاقات التالية:
(∞)ESS + a = (∞)ESS
b x (∞)ESS = (∞)ESS
إذا كانت a و b ضمن جميع الأرقام الحسابية، فإنه لا يوجد أي رقم محدود على الإطلاق يمكنه أن يجعل تلك العلاقة صحيحة. ولأن اللانهاية يمكن كتابتها بهذا الشكل في هاتين المعادلتين ويتم قبولهما، لهذا السبب على وجه التحديد، فإنها لا يمكن أن تتحقق اللانهاية في الواقع المادي الفيزيائي؛ لأنها – إن صحت – فستفشل في الخضوع لقوانين حفظ الطاقة الفيزيائية. وعلى النقيض من ذلك، يتميز الصفر – الذي يماثل اللانهاية – بالعلاقات الآتية:
(0)ESS + a = a
b x (0)ESS = (0)ESS
إذا كانت a و b ضمن جميع الأرقام الحسابية، فلا بد أن يكون الصفر في المعادلة الأولى أمرًا غيرَ مادي؛ لأنه – حتى وإن كان موجودًا بمعنى مادي ما – فلن يكون له أي تأثير مادي على الإطلاق. لذلك فهو غير موجود في العالم المادي الفيزيائي. وهكذا، فكما فرضنا عددًا كبيرًا جدًا ورمزنا له بالرمز VL(∞)، فيمكننا أن نفرض عددًا صغيرًا جدًا ونرمز له بالرمز (0)VS ويمكن أن نعتبره في الفيزياء كالصفر أو العدم المطلق إذا كان سيلبي حاجاتنا لأجل الأغراض العملية والتجريبية. لقد تم مؤخرًا اقتراح فكرة معادلة بشكل أساسي بواسطة الباحث جيسين Gisin.
ولذلك، فإن الفيزياء القائمة الحالية لا يبدو أن اللانهاية الواقعية ESS(∞) أو العدم المطلق (0)ESS لا يبدو أنهما يلعبان فيها أي دور على الإطلاق. رسالتنا الرئيسية إذن التي نريد قولها هي أنه لا يمكن أن توجد لانهاية متحققة بالفعل في الفيزياء أو علم الكونيات، بل ولا حتى على المستوى الأساسي: وهو ما يجب أن يؤخذ كمعيار يوجهنا في اختيار النظريات. وهذا يقودنا إلى اقتراح معيار الاتساق في أي نظرية أساسية في الفيزياء:
(∞)VL ≅ (∞)ESS ↔ (0)ESS ≅ (0)VS
وهذا يعني أنه في النظرية الأساسية لا ينبغي أن يكون هناك على المستوى العملي صراع بين هاذين المفهومين للانهاية الكبيرة واللانهاية الصغيرة.
في حسابِ التفاضلِ والتكامل، كان العالِمُ الألمانيُّ لايبنتز «Leibniz» والفرنسيُّ كاوتشي «Cauchy» قد عرّفا في الأصلِ مشتقةَ (أي تفاضلَ) الدالةِ على أنَّها حاصلُ قسمةِ عددين متناهيين في الصغر. وبعيدًا عن هذا الحدس، لم يتمكنْ لايبنتز ولا كاوتشي من منحِ مصطلحِ “متناهيين في الصغر” معنًى محددًا. وفي الواقع، أدانها عالمُ الرياضياتِ الألمانيُّ جورج كانتور «Georg Cantor» في القرن التاسعَ عشرَ، ووصفَها بأنَّها «بكتيريا الكوليرا» في الرياضيات
تمَّ حلُّ تلك المفارقاتِ والمعضلاتِ التي لا مفرَّ منها في طريقةِ التفكيرِ تلك، عندما قدَّم كارل فايرشتراس «Karl Weierstrass» ما يُشارُ إليه الآن باسمِ طريقةِ إبسيلون-دلتا (ε,δ)، وهو إجراءٌ محددٌ يأخذُ فيه المرءُ بعينِ الاعتبارِ متسلسلاتٍ من النتائجِ التي تقتربُ دائمًا من النتيجةِ النهائيةِ بشكلٍ متناقصٍ باستمرار، ولكنها لا ولن تصلَ إلى الصفرِ فعليًا. وبعد هذا الحلِّ، تم تحديدُ فكرةِ المشتقةِ بشكلٍ جيد، بحيثُ ينطبقُ معيارُ الاتساقِ الذي حددناه على عملياتِ الاشتقاقِ التي نقومُ بها. حوَّل هذا الاكتشافُ حسابَ التفاضلِ والتكاملِ إلى علمٍ تحليليٍّ منضبطٍ في واحدةٍ من أعظمِ التحولاتِ في تاريخِ الرياضيات. لاستخدامِ هذه المفاهيمِ في الفيزياءِ والهندسة، فإنَّ كلَّ ما نحتاجه هو قيمٌ صغيرةٌ كافيةٌ لـ ε وδ تمكنُنا من الحصولِ على النتيجةِ بالدقةِ المطلوبةِ التي تناسبُنا
يتوافقُ هذا الانتقالُ في حسابِ التفاضلِ والتكاملِ إلى تلكَ الدقةِ التحليليةِ في الرياضياتِ مع الانتقالِ في الفيزياءِ من استخدامِ المفهومِ الرياضيِّ لللانهايةِ (∞) إلى كونه رمزًا أو إشارةً إلى «عددٍ محدودٍ» ولكنه عددٌ كبيرٌ (N)، والذي يحلُّ بشكلٍ عمليٍّ محلَّ اللانهاية. نؤكِّدُ أنه في كلِّ الحالاتِ والمواضعِ الفيزيائيةِ التي يُستخدم فيها رمزُ اللانهايةِ (∞) في أيِّ سياق، يُنظرُ إليه كأنَّه عددٌ كبيرٌ جدًا (N)، والذي سيكونُ كافيًا لنا لإجراءِ كلِّ حساباتِنا وتجاربِنا؛ وذلك لأنَّ الواقعَ الماديَّ الفيزيائيَّ الحقيقيَّ يتجسَّدُ في هذا الرقم.
الانهاية الصغيرة جدًا
إنَّ كلَّ النظريات الفيزيائية الناجحة حتى الآن، بما في ذلك نظرية المجال الكمومي على وجه الخصوص، تقوم على افتراض أن الزمكان كمٌّ مُتَّصِلٌ (continuum). إن التناقضات وعدم الاتساق الذي نواجهه يرجع سببه إلى محاولتنا لتعميم تلك النظريات المعروفة لدينا على الأشياء الكبيرة جدًا أو الصغيرة جدًا، حينها تظهر لنا تلك التناقضات وعدم الاتساق بشكل كبير، وهو ما يدل على أن فرضنا بأن الزمكان كم متصل لا يبدو أنه فرض قابل للتطبيق في الواقع العملي. ولهذا السبب، تفترض معظم المناهج المستخدمة في نظرية الجاذبية الكمومية أن الزمكان كمٌّ مُنفصلٍ إلى حد ما، وأن هناك أصغر وحدة لقياس الطول (0)VS (يُفترض عادةً أنه طول بلانك ≈ 10-33 متر)، والذي لم تعد فيه النظرة إلى الزمكان باعتباره كمًّا متصلًا نظرة لا تبدو منطقية أو مقبولة. ومع ذلك، ففي محاولاتنا المستمرة للتوفيق بين نظرية الكمّ ونظرية النسبية العامة لأينشتاين لم يظهر أي اتفاق حتى الآن حول كيفية الوصول إلى هذا قيمة تلك المسافة الأصغر على الإطلاق.
في نظرية المجال الكمومي، يُفترض أن الجسيمات الأولية كأنها أشباه نقاط (point-like)، وهذا الفرض يؤدي بعد ذلك إلى اضطرابات في حساباتنا. ولكن السؤال المهم: هل توجد هذه الجسيمات في الواقع فيزيائيًا؟ أم أن تلك الكميات والجسيمات توجد بعدد كبير جدًا جدًا VL(∞) في مساحة أو في حجم محدود ونهائي في هذا الزمكان الذي هو عبارة عن كَمَّات منفصلة؟
للتعامل مع اللانهائيات، تم تطوير إطار رياضي متقن يُعرف باسم نظرية استبدال اللانهايات «Renormalization Theory» على مدار السنوات السبعين الماضية لإزالة افتراض الطاقات اللانهائية (UV) من الكميات الفيزيائية لتجنب تلك التناقضات وعدم الاتساق في حساباتنا. ومع ذلك، يبدو من الواضح أن هذه ليست الكلمة الأخيرة. في الواقع، وعلى الرغم من النجاحات المذهلة نظرية استبدال اللانهايات، يبدو أن النموذج القياسي لفيزياء الجسيمات (standard model) لا يمكن تطبيقها على الطاقات الكبيرة جدًا، وبالتالي فهو في حاجة إلى استكمال وتحسين لتطبيقه على مستوى الطاقات الكبيرة جدًا. وهذا الكلام ينطبق بشكل أكبر على نظرية أينشتاين، التي لا يمكن استبدال اللانهايات بها. لذلك يبدو أن الأمل الوحيد في تحقيق فرضيتنا – في المعادلة الثالثة – في إطار نظرية المجال الكمومي هو إيجاد نظرية حيث يتم إلغاء كل اللانهائيات بشكل إعجازي.
إن المناهج الحالية في التعامل مع الجاذبية الكمومية تحاول معالجة مشكلة اللانهائية بطرق مختلفة. إن نظرية الأوتار، التي تعتبر على نطاق واسع المرشح الأكثر وعدًا لإكمال الفيزياء فيما يخص مجال الطاقات العالية، تفعل ذلك من خلال إذابة أو إزالة تلك الجسيمات التي تشبه النقاط وتعوضها ببديل عنها إلى أشياء أخرى ممتدة (أوتار)، كما تعتمد على خاصية رياضية دقيقة، وهي الثبات المعياري، للكميات التي تفترضها في الطاقات العالية. وفي حين توجد دلائل تشير إلى أن الزمكان الكلاسيكي قد ينشأ بصورة ما مِن أحد الصياغات غير المضطربة والأكثر جوهرية (والتي لا تزال غير معروفة حتى الآن)، فإن نظرية الأوتار في شكلها الحالي لا تستطيع أن تفسر على وجه التحديد ما يحدث للمكان والزمان على مستوى بلانك. وعلى النقيض من ذلك، تفترض الجاذبية الكمومية الحلقية «Loop Quantum Gravity» منذ البداية بنية منفصلة تحول المكان (والزمان) إلى ما لا نهاية له من شبكات الحلقات، وهي السمة التي تتطلبها بشكل أساسي في عملية التكميم. وبالتالي، فإنها تعتمد على اللانهاية الواقعية ESS(∞) وتعطي لها مكانة مركزية في صياغة النظرية ذاتها. وقد منعت هذه الخاصية حتى الآن هذا النهج من استعادة الزمكان باعتباره كما متصلًا وتوفيقه مع معادلات أينشتاين بأي صورة تقريبية يمكن أن توصلنا إلى حلول فعالة. وهناك أفكار أخرى (مثل الأمان المقارب Asymptotic Safety).. رغم ذلك كله، فإننا لا نزال بعيدين عن الاقتراب أو الوصول إلى اتفاق على الحل الصحيح لتلك المشكلات.
اللانهاية الكبيرة جدًا
بدلاً من مواجهةِ المشكلاتِ التي تنشأُ نتيجةَ الادعاءِ بأنَّ الفضاءَ لا نهائيٌّ، مما يؤدي بالضرورةِ إلى غيابِ أيِّ حدودٍ للمسافاتِ المكانيةِ بينَ مختلفِ أجزاءِ الكونِ، فإنه في هذه الحالةِ لا يمكننا الاعتمادُ على مفهومِ اللانهايةِ بالشكلِ الذي يُرمَزُ له بـ VL(∞): حيثُ إنَّ الزعمَ بوجودِ عددٍ لا نهائيٍّ من المجراتِ في نموذجِ الكونِ هو تشويهٌ صارخٌ للحقيقةِ، إذ إنَّ الكونَ الماديَّ الذي نعرفهُ يقتصرُ على عددٍ محدودٍ من المجراتِ. والنقطةُ المحوريةُ هنا، كما تمَّ الإشارةُ إليها سابقًا وممثلةً في المعادلةِ الأولى، هي أنَّ مفهومَ اللانهايةِ ليسَ مجردَ تمثيلٍ لعددٍ كبيرٍ جدًا؛ بل هو كيانٌ ذو طبيعةٍ مختلفةٍ تمامًا لا يمكنُ مقارنتُه بالأعدادِ الكبيرةِ. ومع هذا الادعاءِ، ستفشلُ معادلتُنا الثالثةُ (التي تشترطُ الاتساقَ) مرةً أخرى. فهل عددُ المجراتِ في الكونِ لا نهائيٌّ؟ الجوابُ هو لا، إذا كانت المقاطعُ المكانيةُ للكونِ محدودةً، وهذا صحيحٌ بشكلٍ ضروريٍّ إذا كانت تلكَ المقاطعُ منحنيةً إيجابيًا، ولكنَّهُ ممكنٌ أيضًا في حالةِ المقاطعِ المسطحةِ أو المنحنيةِ بشكلٍ سلبيٍّ. إنَّ حجةَ هيلبرتَ تقودُنا إلى استنتاجٍ مفادهُ أنَّ الكونَ يجبُ أن يكونَ في الواقعِ محدودًا من حيثُ المساحةُ، وأنَّ كميةَ المادةِ فيهِ محدودةٌ، وكذلكَ عددُ المجراتِ وعددُ الكائناتِ الحيةِ.
بالتأكد من حق البعض أن يعترضوا قائلين: حتى لو افترضنا حقيقةً أن الكون هو لانهائي بالفعل، فإنه لا يمكننا أبدًا إثبات ذلك؛ لأننا – وإن تجاهلنا المشكلة الأساسية بأن هناك حدودًا لرؤيتنا البصرية – وافترضنا أنه بإمكاننا رؤية عدد لا نهائي من المجرات، فلن نستطيع بأي حال من الأحوال عدّها؛ فمهما بلغ عدد المجرات التي قمنا بعدّها، فلن نكون قد أحرزنا أيَّ تقدم في إظهار أو إثبات أن هناك بالفعل عددًا لا نهائيًا من الكيانات. ستظل هناك لانهائية بانتظار العدّ. هذه هي طبيعة اللانهاية المتحققة بالفعل ESS(∞). إن مثل هذه الادعاءات التي لا يمكن اختبارُها يجب أن تُعامل بشكّ وتحرز شديدين: فهي مثال آخر على الادعاء بنتائج يُزعم أنها علمية ولكنها غير قابلة للاختبار ولا التحقق منها.
أكثر الادعاءات جموحًا وتطرفًا هي تلك التي تتعلق بفكرة وجود عدد لا نهائي من الأكوان «multiverse». فهل هناك بالفعل عدد لا نهائي من الأكوان المتوسعة التي تشبه كوننا، ولكنها تختلف في تفاصيل مثل قيمة الثابت الكوني أو ثابت البنية الدقيقة؟ نظرًا لوجود حدود لرؤيتنا البصرية كما ذكرنا سابقًا، لا يمكننا إثبات صحة هذا الادعاء من خلال الملاحظة المباشرة (ولا حتى غير المباشرة). يعتمد هذا الرأي إما على تفكير فلسفي مرتبط بمسائل أنثروبية، (مثل محاولة تفسير سبب ملاءمة الكون للحياة)، أو على ادعاءات بأن الفيزياء الحالية – خاصة المتعلقة بنظرية التضخم الكوني – تتطلب وتقتضي بالضرورة وجود هذه الأكوان. ومع ذلك، فإن الفيزياء التي يُزعم أنها تدعم هذه الفكرة ليست مثبتة بشكل جيد ولا مختبرة ومجربة بشكل كافٍ، بل هي ليست تجريبية من الأساس. بالإضافة إلى ذلك، تواجه حساب الاحتمالات التي يُفترض أنها تدعم هذه الفكرة مشاكل كبيرة؛ لأن وجود عدد لا نهائي ESS(∞) من الأكوان يجعل من المستحيل الوصول إلى أي حساب احتمالي دقيق وواضح.
الادعاءات بوجود عدد لا نهائي من النسخ المماثلة لنا في أكوان أخرى هي إدعاءات لا يمكن إثباتها بحال، سواء كانت تستند إلى فكرة أن الكون الذي نراه هو كون لانهائي، أو إلى وجود أكوان متعددة لا نهائية. ولا تختلف هذه الحال عن غيرها من الحالات الأخرى التي يُلجأ فيها إلى مفهوم اللانهائية المتحققة بالفعل، فإن هذا كله ليس علمًا يمكن اختباره ولا تجريبه؛ إذ يعتمد على اللانهاية المتحققة في الخارج ESS(∞) وخصائصها المتناقضة. لذلك، فإنه لا يلبي المعيار الثالث (وهو الاتساق) الذي نقترحه كشرط للصحة أو القابلية للتطبيق.[1]
| الدور | الاسم |
|---|---|
| إعداد | خالد أ. الشهالي |
| ترجمة | محمد رضا |
| مراجعة علميَّة | خالد أ. الشهالي |
| تدقيق لغويّ | خالد أ. الشهالي |
| تحرير | خالد أ. الشهالي |
| تصميم | خالد أ. الشهالي |

