«العالم المسطح ــflat land»«مدخل إلى البعد الرابع»
الرياضيات ليس لها حدود وغير مقتصرة فقط على عالمنا بل تتخطاه مبتعدة إلى توصيف عوالم أخرى ليس بمقدورنا إدراكها واقعيا ولكننا يمكننا أن نتصورها في مخيلتنا قياسا على عالمنا ثلاثي الأبعاد .
« البعد الرابع من منظور رياضي »
ربما سمعت هذا المصطلح من قبل «البعد الرابع ــ fourth dimension» . حيث اقترن ذكره بأحد أكثر الاكتشافات العلمية أهمية في تاريخ المعرفة الإنسانية والتي لاقت صدى كبيرا في الأوساط العلمية إلى يومنا هذا وهو اكتشاف نسبية الزمن حيث أنه لم يعد قيمة مطلقة بل أصبح كمية متغيرة أخرى تضاف إلى الأبعاد الهندسية الثلاثية في عالمنا لتوصيف نقطة ما في الفراغ توصيفا دقيقا .
البعد الرابع الذي سنتناوله الآن هندسيا هو بعد مكاني إضافي ، وجوده يمثل وجود الفراغ رباعي الأبعاد أو بتفصيل أكثر يمكننا تسميته الفراغ الإقليدي رباعي الأبعاد .ويمكننا توصيفه عن طريق تعميم مفاهيم وأسس الفراغ الإقليدي ثلاثي الأبعاد .
ولفهم أفضل سنشرع في توضيح بعض أساسيات الفراغ الإقليدي ثلاثي الأبعاد:
- النقطة:
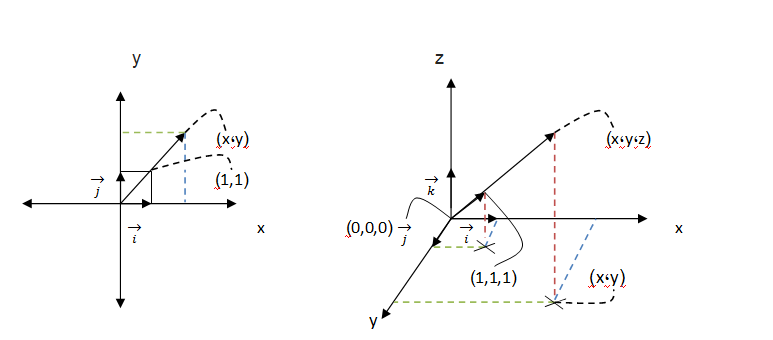
هي فقط فكرة تخيلية وهي عبارة عن كائن رياضي عديم الأبعاد والمساحة والحجم وتمثل مفهوما أساسيا في الهندسة والرسومات الإشعاعية و تمثل معلومات عن الموقع فقط دون أي خواص رياضية أخرى. وهي وحدة البناء الأساسية لكل الأشكال الهندسية .وفي الرياضيات يمكن تعريف الفراغ على أنه عدد لانهائي من النقاط .في الهندسة المستوية(الفراغ ثنائي الأبعاد) يرمز للنقطة بثنائية مرتبة من الأعداد (y,x) وفي الفراغ ثلاثي الأبعاد بثلاثية مرتبة من الأعداد(z,y,x) حيث يمثل العدد الأول الإحداثي الأفقي والعدد الثاني الإحداثي الرأسي والعدد الثالث إحداثي مستوى عمودي على كل من الإحداثيين السابقين.
- المستقيم:
هو خط مباشر له طول لانهائي وعرضه يؤول للصفر ويمكن تمثيله بعدد لانهائي من النقاط ويمكن توصيفه أيضا بأنه ناتج تقاطع مستويين لانهائيين غير متوازيين .
- القطعة المستقيمة:
القطعة المستقيمة عبارة عن مجموعة نقاط مصفوفة على بعد واحد.ومحدودة بمقدار معين من أطوال القياس.
- البعد:
البعد هو اتجاه و يمكننا تصوره على انه خط ، ولكنه متجه أي شعاع ، ولكي يتميز عن باقي الخطوط العادية باعتباره خط استثنائي لابد وان يكون عموديا على أي من الأبعاد الأخرى التي تستخدم لتوصيف نقطة ما، سواء كانت على نفس البعد فهي عمودية على البعد الصفري أو مستوية أو في فراغ ثلاثي الأبعاد أو رباعي أو أكثر . أو بمعنى آخر يعرف لمكان أو جسم بالحد الأدنى للإحداثيات اللازمة لتحديد نقطة في داخله.وهو عبارة عن خط مستقيم يحتاج شرط التعامد على خط مستقيم آخر (بعد آخر) ليشكل الحد الأدنى من الإحداثيات لتوصيف لنقطة معينة .
- الأشكال الهندسية المسطحة:
هي الأجسام الثنائية الأبعاد كالمثلث والمربع والدائرة تتألف من مجموعة قطع مستقيمة تقع في مستوى واحد يمكن تمثيله ببعدين هندسيين.
- المُتَّجَهْ:
يمكن تمثيله رياضيا بسهم يتجه من نقطة إلى أخرى حيث تمثل قاعدة السهم نقطة البداية ورأس السهم تمثل نقطة النهاية.ويتحدد كل متجه بثلاثة عناصر رئيسية المقدار وهو كمية قياسية تمثل بطول المتجه والاتجاه ويمكن تحديده في المستويات ثنائية الأبعاد بزاوية ميله على أحد البعدين الأفقي أو الرأسي وفي الفراغ ثلاثي الأبعاد يمكن تمثيله باستخدام زوايا أويلر ونقطة التأثير.نقطة بداية السهم.
متجه الوحدة:


بعد هذا التوضيح يمكننا الآن الانتقال إلى مقدمة كتاب «الأرض المسطحة ــflatten earth » هي رواية قصيرة للكاتب الانجليزي« إدوين أبوت ــEdwin Abbott »1844» .والتي تمثل مدخلا شيقا للعالم متعدد الأبعاد. هي حقيقة تجربة رياضية مَرِحَة توضح المِحَنْ والمعاناة للكائنات ثلاثية الأبعاد في البعد الثنائي أو المسطح . حيث يبدأ حديثه قائلاً:
نحن نعيش في عالم ثلاثي الأبعاد حيث أن كل شيء له طول وعرض وارتفاع ولكن ماذا لو كان عالمنا ثنائي الأبعاد؟ فلنذهب معا في هذه الرحلة المثيرة لنتعرف سويا على خصائص هذا العالم والذي سيمكننا من استيعاب مفهوم البعد الأكبر (الرابع) فلنتخيل أن هذا العالم سحق بواسطة آلة رصف الطرق لتجعل هذا العالم كله منحصرا في مستوى ثنائي الأبعاد (افتراضيا بالطبع ! ) كيف سيبدو هذا العالم ؟ وكيف سنشعر وسنرى الأشياء والمجسمات المختلفة التي اعتدنا على رؤيتها مثل الكرة والهرم والمكعب والمخروط والاسطوانة وغيرها؟
حسنا الآن من هم قاطني العالم ثنائي الأبعاد؟ وما هي قواعده ؟
هنالك عدد كبير جدا نعرفهم بالطبع وهي جميع الأشكال الهندسية المستوية المألوفة لنا جميعا مثل المربع والمثلث والمستطيل والخماسي وغيرها من الأشكال المضلعة إلى أن تؤول هذه الأضلاع إلى عدد لانهائي فنحصل على المنحنيات المستوية وأشهرها الدائرة .
وكل هذه الأجسام تعيش في عالم ثنائي الأبعاد وترى بعضها البعض كقطع مستقيمة. فهي تألف البعد السيني والصادي( x,y) وتبرمج عقلها على أن الكون كله مُؤَلَّفٌ من بعدين فقط. وتستطيع التحرك يميناً ويساراً, وشمالاً وجنوباً. لكنها لا تستطيع أن تتحرك, ولا أن تتخيل, الاتجاه الأعلى والأسفل. و إذا أخبرها أحد عن وجود عالم آخر فيه كائنات ثلاثية الأبعاد ويتم توصيفها ببعد إضافي آخر ( x,y,z )لا أحد منهم يسعه تخيل الأجسام ذات الثلاثة أبعاد مثل المكعبات والأهرام والكرات, ولا يستطيع أن يراها.
رغم أنها موجودة في عالم حقيقي . وسرعان ما سينكرون وجوده إذا ادعى احدهم بوجوده وذلك لأنه ببساطة ليس جزءا من عالمهم أو تجربتهم ولكن كل ما يحتاجونه فهم أحد هذه الكائنات الثلاثية إذا ظهر في عالمهم ، هو بعض المفاهيم البسيطة .
إذا نظرت لهذا المستوى من أعلى ستجد إسقاطات هذه الأشكال واضحة كما نعرفها ولكن داخل العالم المسطح هم لا يرون بعضهم إلا على صورة قطاعات مستقيمة ..الباهتة منها علامة للبعيد و الواضحة منها علامة للقريب ، والأطوال لتمييز المساحات ، والألوان للاختلافات بين الأشكال . فهم يُوَصِّفُون الأوضاع تماما بناءا على معطيات عالمهم . ويوما ما ظهر مجسم ثلاثي الأبعاد في عالمهم إنه حقا مجسم مميز وهو الكرة . ولكن كيف سيلاحظ وجودها من يعيش في المستوى الثنائي ؟ كيف ستبدو له المجسمات الثلاثية من داخل حجرته المستوية الصغيرة ؟ كان أحد قاطني العالم المستوي وهو المربع ، بطل هذه القصة ، جالسا بالصدفة فلاحظ وجود شيء غريب لم يعهده من قبل . لقد رأى دائرة ظهرت من العدم وأخذت تكبر وتصير أكبر مع مرور الوقت ثم استقرت لحظيا على طول معين ثم بدأت تصغر وتصغر حتى اختفت تماما مرة أخرى .! وتكرر حدوث ذلك مرة أخرى ..! هنا أصيب المربع بالذعر ولم يعد يعلم إن كان ما يراه حقيقي فعلا أم مجرد خيالات ؟ . فجأة سمع المربع صوتا يناديه : مرحبا أيها المربع ..! كيف حالك ؟ . زاد خوف المربع الآن أنها ليست خيالات ولكن ما يمر به حقيقي وهو بصدد التعرف على هذه الدائرة الخارقة التي لها قدرة عجيبة على تغيير شكلها زيادة ونقصانا.
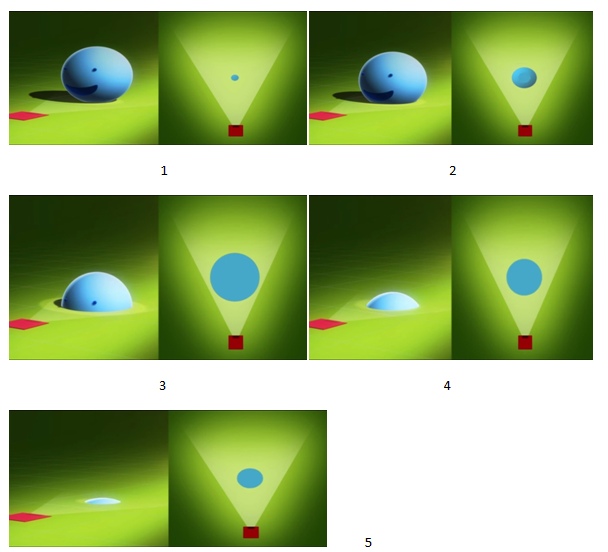
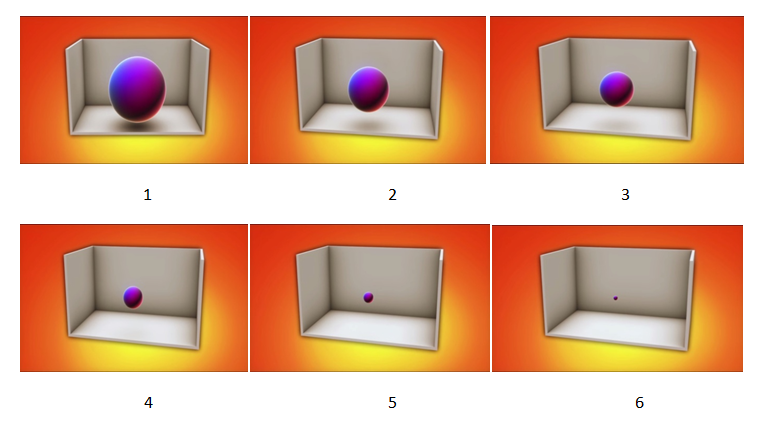
قال لها أنا بخير كيف حالك أيتها الدائرة العجيبة! فضحكت الكرة في غرور قائلة أنا لست بذلك الصغر! .حقيقةَ أنا عبارة عن عدد لانهائي من الدوائر مختلفة الأقطار . ويسمونني الكرة وأنا لا أنتمي إلى عالمكم الصغير ثنائي الأبعاد أنا من عالم آخر أكبر بكثير من عالمكم ، يسمى العالم ثلاثي الأبعاد. وأستطيع رؤية عالمكم وأشكالكم بطريقة أفضل مما ترون أنفسكم. يا للعجب ..! ذهول المربع الآن لا يُوصَف لابد وانه يوم حظه ليتعرف إلى كائنات من عالم آخر . قال لها إذاً ما الذي يحدث بالضبط لماذا أراكي بهذه الطريقة تظهرين وتختفين فجأة ؟ . أدركت الكرة ما يقصده المربع فقالت له أنا حقيقة عندما أزور عالمكم فإني أقطعه عابرة من أحد وجهيه إلى الوجه الأخر المقابل له. وأثناء مروري منه لا تستطيع أن ترى مني سوى إسقاطات الدوائر اللانهائية التي أتكون منها .كل برهة من الزمن سترى إسقاطا لدائرة معينة أكبر أو أصغر من سابقتها وأختفي تماما حينما لا يوجد جزء مني يتقاطع مع عالمكم.
هذه الأشكال المختلفة للكرة التي سيراها العالم الثنائي الأبعاد في صورة مقاطع عرضية لمجسم الكرة أثناء مرورها بالسطح ثنائي الأبعاد في كل وضعية شكل مختلف بالنسبة للراصد من الأعلى وبالنسبة لسكان العالم الثنائي على السواء .
ثم أخذت الكرة صديقها المربع معها في اتجاه الارتفاع حيث لم يذهب هنالك أحد من قبل هنا تستطيع رؤية كل شيء المجسمات والمباني وتنظر إلى العالم ثنائي الأبعاد فستجده مسطحا لأول مرة تصاب بالذهول من الأشكال الجديدة لأصدقائها من المثلثات والمربعات والتي تبدوا له .الآن غريبة تماما .
ولما صعقه ما أدركه من جمال في العالم الثلاثي طلب من صديقته الكرة أن يزور العالم رباعي الأبعاد والأبعاد الأعلى منه. وهنا غابت ابتسامة الكرة ورفضت تماما ما قاله المربع من افتراءات بوجود عوالم أخرى غير عالمه و بسرعة أعادت المربع إلى عالمه ثانية. سخط الكرة مبرر الآن فالبعد الرابع يبدوا صعبا على الكرة أن تتفهمه فهو من خارج عالمها. وتلعب الصدفة دورها مرة أخرى ، فبينما الكرة جالسة حزينة يملؤها الحيرة إذا كان هنالك عالم آخر ليس في إدراكها غير عالمها الذي عهدته إذا بصديق جديد يلوح في الأفق ،«الكرة الرباعية الأبعاد ــ hyper sphere» فكان لدى الكرة نفس إحساس المربع في البداية ولم ترى الجزء المخفي منها مثلما مرت الكرة الثلاثية من المستوى الثنائي زادت تدريجيا في طول المقطع وقطر الدائرة إلى أكبر نقطة ثم أخذت في الانكماش إلى أن مرت تماما خارج المستوى يمكننا التعبير عن هذه الزيارة العابرة بمجموعة لانهائية من القطاعات العرضية إذا يمكننا فعل نفس الشيء في العالم الثلاثي مع المجسمات الرباعية الشكل. دعنا نقول أن أل hyper sphere هي الشكل المناظر للكرة في العالم رباعي الأبعاد فإذا مرت في عالمنا الثلاثي فتبدو مثل شكل الكرة ولكننا لن نرى الجزء الآخر المخفي منها ، هنا أدركت الكرة الثلاثية أن علمها محدود ومن الممكن أن يكون هنالك عالم كامل بكائنات رباعية الأبعاد وأشكال حياة لها خصائص رباعية الأبعاد ، في الواقع ربما يكون هنالك عوالم كاملة مخفية عنها تماما ولا تستطيع إدراكها وذلك طبقا لطبيعتها الثلاثية الأبعاد .
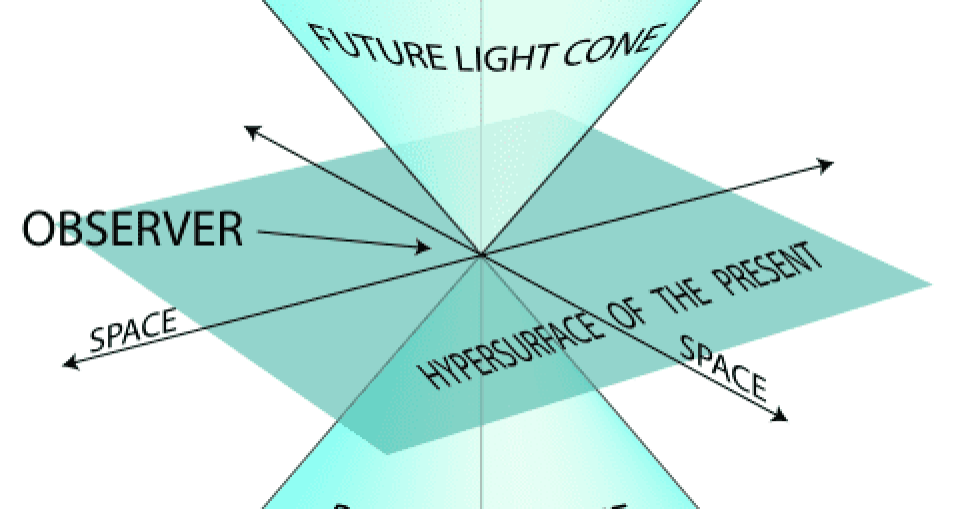
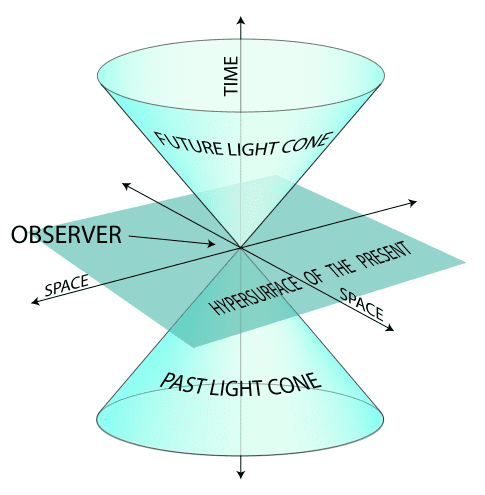
يمكننا الان تخيل أحد أكثر الأشكال الهندسية أهمية في النظرية النسبية وهو : المخروط الضوئي (light cone ) الرباعي الأبعاد
4Dimensional light cone
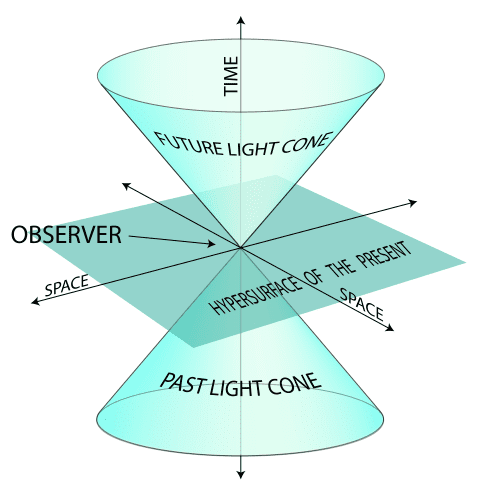
والذي يعرف على أنه المسار الذي يتبعه وميض شعاعي ضوئي منبثقا من حدث مفرد زمكاني Event ، يتم تحديده عن طريق نقطة وحيدة في الفضاء ولحظة معينة من الزمن (المخروط الضوئي في الماضي past light cone ) حتى وصوله إلينا باعتبارنا الملاحظ observer في الحاضر Present ومتخطيا موقعنا في الزمكان المنحني إلى المنطقة المستقبلية future light cone . يمكنك تشبيهه بخط زمني time line للأحداث من قيمة معينة سالبة ولتكن مالا نهاية إلى قيمة معينة أخرى ولتكن موجب مالانهاية . حيث نقع نحن في موقع النقطة الصفرية التي تمثل الحاضر . والمخروط الضوئي اكتسب شكله الافتراضي الثلاثي الأبعاد لأجل عملية التبسيط . حيث افترضنا أن الضوء يتحرك على شكل دائرة في جميع الاتجاهات في مستوى ثنائي الأبعاد وليس فراغا ثلاثي الأبعاد . كل حدث مفرد في الكون Event يمكن تمثيله بدائرة مختلفة وبأقطار مختلفة بعدد لانهائي من الأحداث والدوائر . والواقع أن هذه الدوائر هي اختزال للفضاء الكروي الثلاثي المتماثل symmetric 3D spherical space أو السطح القطعي Hyperbolic surface . بمعنى أن أي قطاع دائري في المخروط الضوئي هو فراغ ثلاثي الأبعاد .وبتمديده في البعد الزمني نحصل على الفراغ الرباعي الأبعاد .
إعداد : Ahmed Hosiny
المصادر :
- Ambinder, Michael S., Ranxiao Frances Wang, James A. Crowell, George K. Francis, and Peter Brinkmann, ‘Human Four-Dimensional Spatial Intuition in Virtual Reality’, Psychonomic Bulletin & Review, 16 (2009), 818–23 <http://dx.doi.org/10.3758/PBR.16.5.818>
- ‘Flatland and Its Sequel Bring the Math of Higher Dimensions to the Silver Screen’, Science News <https://www.sciencenews.org/article/flatland-and-its-sequel-bring-math-higher-dimensions-silver-screen> [accessed 20 September 2015]
- ‘Flatland Animation: The Project’, Flatland Animation <http://flatlandanimation.blogspot.com.eg/2011/05/project.html> [accessed 20 September 2015]
- Forsyth, A. R., Geometry Of Four Dimensions Vol I (At The University Press., 1930) <http://archive.org/details/geometryoffourdi032760mbp> [accessed 20 September 2015]
- Hinton, Charles Howard, The Fourth Dimension (London : G. Allen & Unwin Ltd, 1912) <http://archive.org/details/fourthdimension00hintarch> [accessed 20 September 2015]
- Jos Leys, Dimensions Chapter 1 <https://www.youtube.com/watch?list=PL3C690048E1531DC7&v=6cpTEPT5i0A> [accessed 20 September 2015]