مقدمة
في هذا الجزء من سلسلتنا ميكانيكا الموائع نتحدث عن شعور اعتاد معظمنا اختباره حين ينزل إلى البحر أو إلى المسبح، فنشعرُ أننا أخف مما نحن عليه، وربما دفَعنا ذلك الشعور إلى أبعد حدوده فجربنا بعض التمارين الصعبة تحت الماء، مثل الضغط، ورفع الأثقال، والسؤال هنا: هل فعلًا وزن الأجسام تحت الماء يكون أخف مما هو عليه إذا ما قيس في الهواء؟
وللإجابة عن هذا السؤال دعونا نحضر جسمًا معلوم الوزن مسبقًا ونحضر ميزانًا زنبركيًا مضادًا للمياه، إذا وزنا الجسم في الهواء ثم وزناه تحت الماء سنجد أن وزنه في الماء أقل منه في الهواء، والسر وراء تلك الملاحظة هي ظاهرة «الطفو».
الطفو وقانون أرشميدس
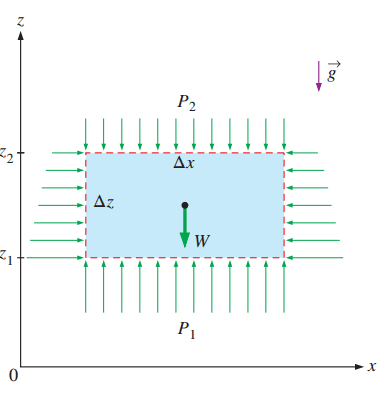
دعنا لا نضع معادلة قوة الطفو مباشرةً، ولنفترض أننا لا نعلم أي شيء عن تلك القوة. استعرضنا الصورة التالية في المقال السابق، وقلنا إن هذا النظام -والذي هو مجرد حيز من الماء له شكل مستطيل- ساكن لا يتحرك، إذًا لابد لمحصلة القوى المؤثرة عليه أن تكون مساوية للصفر. دعونا نحسب محصلة القوى العمودية فقط هنا:
![]()
والحد الأخير المطروح في المعادلة ما هو إلا وزن المياه المحصورة في ذلك النظام. هَبْ أني وضعت صندوقًا من الفولاذ في الماء، واعتبرت أن هذا الصندوق هو نظامي الجديد الذي أنا بصدد دراسته، سأجد أن معادلة محصلة القوى العمودية المؤثرة عليه هي:
![]()
حيث F هي القوة المحصلة التي نحن بصدد حسابها، وإذا طرحنا المعادلة الأولى من المعادلة الثانية سنصل إلى قيمة القوة المحصلة بسهولة:
![]()
حيث إن V هي حجم الجسم، وهو يساوي ΔxΔyΔz. والعالم بكثافة كلٍ من الماء (997kg/m3) والفولاذ (8020kg/m3) سيجد أن قيمة هذه القوة سالبة، أي أن محصلة القوى تتجه للأسفل، أي أن ذاك الجسم سيغوص. والقيمة المطلقة للمحصلة هي بذاتها قراءة الميزان الزنبركي.
يمككنا أن نبسط الأمر، فنتخيل أن لدينا نظام تؤثر عليه قوتان فقط، قوة وزن الجسم، وقوة الطفو (buoyant force). والمحصلة هي مجموع قوتي الوزن وقوة الطفو (مع أخذ إشارات القوى في الاعتبار أثناء عملية الجمع)، وعليه فإن قوة الطفو تساوي المحصلة F مطروحٌ منها وزن الجسم:
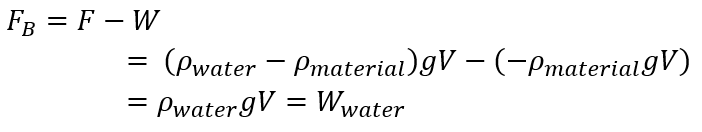
وقوة الوزن حين استعضنا عنها في المعادلة استعضنا عنها بقيمة سالبة؛ لأن قوة الوزن دائمًا اتجاه عملها للأسفل، وقد اخترنا الاتجاه الأسفل ليكون هو السالب. و ρmaterial في المعادلة السابقة هي كثافة المادة أيًا تكن، والتي نحن بصدد دراسة قوة الطفو المؤثرة عليها، وقوة الطفو اتجاه عملها عمودي على سطح الماء، متجهةً إليه. والمعادلة السابقة تعطينا نتيجة واضحة هي نص قانون أرشميدس (287-212 ق. م. ) للطفو والذي ينص على:
إن قوة الطفو التي تعمل على جسم ذي كثافة منتظمة مغمورٌ في سائل تساوي وزن السائل الذي أزاحه الجسم، وتعمل إلى الأعلى. [1]
– أرشميدس.
إذًا عزيزي القارئ، إن كنت من الذين يذهبون إلى البحر ويلعبون بزجاجات المياه الفارغة مُحكمة الغلق، فلا تكرر خطأ من قبلك. إنك حين تجبر تلك الزجاجة على الغوص تحت المياه، ما فعلته هو أنك قمت بالتأثير عليها بقوة أكبر من قوة الطفو، فتكون المحصلة صفرية، لكن بمجرد أن تترك الزجاجة لن تظل في مكانها، لا لأنها لا تريد أن تطيعك، هي فقط قوة الطفو لم تجد القوة الكافية التي تمانعها، فإذا بالزجاجة تتسارع تحت وطأة قوة الطفو باتجاه سطح الماء، لتخرج منه مسرعة وتصدم ما على سطح الماء بقوة، سواء أكان وجهك الذي كان يراقب خروج الزجاجة، أو وجه أحد رفاقك؛ لذا عليك الحذر حين تغطس زجاجة فارغة في الماء.
قبل أن نكمل مقالتنا تلك دعوني أذكركم بأن قوة الطفو تؤثر على كل جسم موجود داخل أي مائع، سواء أكان المائع ماءً أو أي سائل أو أي غازٍ آخر. ومن الأمثلة على ذلك أننا ونحن نقف في أماكننا تؤثر علينا قوة الطفو من قبل الهواء، وقوة الطفو في تلك الحالة تساوي وزن حجم مساوٍ لحجمنا من الهواء. ومثل تلك القوى ضئيلة، فإذا كان وزن أحد الرجال يساوي 774,2 نيوتن، وقمنا بوزنها باستخدام ميزان زنبركي، فإن الوزن المقاس يساوي 773 نيوتن. قد يبدو هذا الفارق بسيطًا بعض الشيء ولا داعي لأخذ قوة الطفو في الاعتبار في هذه الحالة، لكن بالنسبة للأجسام منخفضة الكثافة، فمثل هذا الفارق سيسبب خطأ ملحوظًا في الحسابات؛ لذا لا بد من أخذه في عين الاعتبار.
ظاهرة جبل الجليد
بالنسبة للأجسام الطافية، لا بد أن تساوي قوة وزن الجسم قوة الطفو، لذا لن تجد أي جسمٍ يطفو تمامًا فوق سطح الماء، بل سيبدأ الجسم بالغوص تدريجيًا حتى تساوي قوة الطفو قوة الجسم. وقوة الطفو تزداد كلما نزل الجسم تحت سطح الماء أكثر، لأنه كلما نزل زاد وزن السائل المزاح، وبالتالي زادت قوة الطفو. بعد اتزان الجسم يمكن التعبير عن تساوي قوة الوزن وقوة الطفو بالتعبير الرياضي التالي:
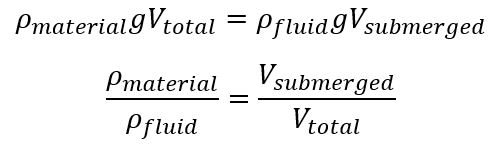
حيث إن ρmaterial هي كثافة الجسم، و ρfluid هي كثافة المائع، و Vtotal هو الحجم الكلي للجسم، و Vsubmerged هو حجم الجزء المغمور من الجسم.
لنأخذ الجليد كمثال عملي: إذا علمنا أن كثافة الجليد تساوي (920kg/m3) وكثافة المياه تساوي (997kg/m3) فإن نسبة الجزء المغمور من الجليد تساوي 920 ÷ 997 أي 92%. أي أنك حين تنظر إلى جبل جليد هائل يطفو فوق سطح الماء، أنت حينئذ تنظر إلى 8% من حجم الجبل الحقيقي!

تطبيقات على الطفو
من الأمثلة الحياتية التي تلعب فيها قوانين الطفو دورًا رئيسيًا هي الغواصات، والغواصات بها عجيبة، حيث تجدها تغطس تارة وتطفو تارة أخرى، لا نستطيع القول أن كثافتها أقل من الماء ولا أكثر منه. الأمر وما فيه أن الغواصات مصممة بخزان أو خزانين، مملوء بالهواء. حين يكون الخزان مملوءًا بالهواء تكون الكثافة الكلية للغواصة أقل من كثافة المياه وبالتالي تطفو الغواصة، أما إن أراد القبطان أن يشرع في عملية الغوص، فإنه يفرغ الهواء من تلك الخزانات حتى تكون الكثافة الكلية للغواصة أعلى من كثافة المياه وبالتالي تبدأ عملية الغوص، والغواصة بها خزان هواء مضغوط لتوفير هواء التنفس لعمالها، ولملء الخزانات مرة أخرى في حال أرادت الغواصة الطفو من جديد.


