
ينتج الشغل عندما تحرك جسمًا ما بقوة لمسافة معينة. والآلات البسيطة تقوم بتوليد قوة أكبر من القوة المبذولة عليها؛ وتعرف المنفعة الآلية بأنها النسبة بين هاتين القوتين. وتأتي هذه المنفعة الآلية على حساب المسافة التي يتحركها الجسم، حيث إنه لا يمكن توليد طاقة من العدم، والشغل ما هو إلا طاقة في النهاية.
وقد استخدمت هذه الآلات الست منذ ألاف السنين، فقد قام أرشميدس بدراسة الفيزياء الكامنة وراءها دراسة كمية. ويمكن ربط وتجميع هذه الآلات ببعضها بتناسق وترتيب معين لتولد منفعة آلية أكبر، كما هو الحال في الدراجة الهوائية.
والعامل المشترك في كل هذه الآلات أنها تستخدم مبدأ حفظ الطاقة، وقانون الشغل والقوة.
![]()
توضح المعادلة السابقة أن وظيفة تلك الآلات هي مضاعفة القوة المبذولة على حساب المسافة التي يتحركها الجسم. فلا يمكن لأي من تلك الآلات أن تخلق طاقة من العدم.
الروافع
تحيط بنا الروافع من كل جانب، بل وتتواجد داخل أجسامنا أيضًا؛ حيث أن الأساس الفيزيائي الذي يحكم عمل الروافع هو نفسه ما تعتمد عليه عضلاتنا وأوتارنا في تحريك أطرافنا. وفي هذا السياق، فإن عظامنا هي بمثابة الكمرات أو العوارض، ومفاصلنا هي بمثابة نقط الارتكاز.
ويُحكى عن أرشميدس أنه قال في ذات مرة: «اعطني وتدًا بالقوة الكافية، وعارضة بالطول الكافي، وسأجعل الأرض بأكملها تتحرك». وذلك حين اكتشف مبدأ عمل الروافع. ومقولته صحيحة نظريًا كشهادة على قدرة الروافع على توليد المنفعة الآلية لولا أنه يسلتزم لتحريك كوكب الأرض رافعة طويلة لدرجة منافية للعقل والمنطق.
(ملاحظة: قد تم نقل هذه المقولة بواسطة ببس الرومي (Pappus of Alexandria) والذي عاش في عصر لاحق، ومن المحتمل أن أرشميدس لم ينطق بهذه المقولة من الأساس.)
ولكن كيف تعمل الروافع؟ وما هي المبادئ التي تحكمها؟
كيف تعمل الروافع
الرافعة هي آلة بسيطة تتكون من جزئين ماديين، وقوتين فيزيائتين:
- كمرة أو عارضة أو أي جسم صلب على شكل عصا.
- نقطة ارتكاز (fulcrum).
- قوة داخلة (أو المجهود).
- قوة ناتجة (أو الحمل أو المقاومة).
يجب أن يستند جزء من الكمرة على نقطة الارتكاز. وفي الروافع التقليدية، تظل نقطة الارتكاز ثابتة في مكان معين بينما تؤثر القوى الأخرى على أماكن أخرى على طول الكمرة. ومن ثم تدور الكمرة حول محور نقطة الارتكاز بحيث تولد قوة خارجة على جسم ما نريد تحريكه لغرض معين.
وينسب الفضل لعلماء الرياضيات اليونانيين القدماء وأرشميدس باكتشافهم قوانين عمل الروافع، والتي قاموا لأول مرة بصياغتها صياغة رياضية.
المبدأ الرئيسي هنا هو أن الكمرة جسم صلب، ومن ثم يتبع أن العزم المؤثر على أحد الأطراف سينتقل بدوره إلى الطرف الآخر، حيث أن الكمرة الصلبة لا تغير من شكلها. دعنا نلقي الضوء على حالة خاصة قبل أن نحاول تطبيق هذا المبدأ على الحالات العامة.
اتزان الأحمال على الروافع
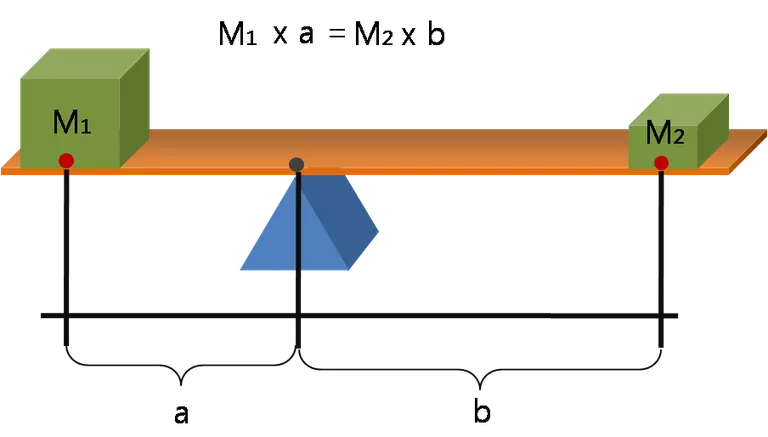
وفي هذه الحالة لدينا أربع كميات في محل اهتمامنا وبوسعنا أن نقيسهم:
- M1: كتلة الحمل الموضوع على أحد أطراف الكمرة (القوة الداخلة).
- a: المسافة بين موضع الارتكاز والكتلة M1.
- M2: كتلة الحمل الموضوع على الطرف الآخر (القوة الخارجة).
- b: المسافة بين موضع الارتكاز والكتلة M2.
هذه الحالة البسيطة تسلط الضوء على العلاقة بين هذه الكميات. وتجدر الإشارة أننا نناقش رافعة مثالية، حيث أننا لا نأخذ قوى الاحتكاك بين الكمرة وموضع الارتكاز في الحسبان، ونتجاهل هنا تأثير العوامل الأخرى مثل تأثير الرياح.
يشبه هذا التركيب إلى حد كبير الميزان ذو الكفتين، والذي تم استخدامه على مدار التاريخ لتحديد أوزان الأجسام. وفيه تتساوى المسافة بين كل حمل وموضع الارتكاز. مما يعني أنه يجب أن يكون كل حمل مساويًا للآخر حتى يتحقق التوازن. فإذا كنت تعرف وزن أحد الأحمال يمكنك تحديد وزن الحمل الآخر.
ما يثير اهتمامنا بالطبع هو حالة عدم تساوي تلك المسافات. فمن الآن فصاعدًا، سوف نفترض أن a لا تساوي b. وفي هذا الموقف، أدرك أرشميدس بالتجربة وجود علاقة رياضية بين حواصل ضرب كل كتلة مع المسافة بينها وبين موضع الارتكاز:
![]()
ومن خلال هذه العلاقة ندرك مثلًا أنه في حالة مضاعفة المسافة بين الحمل وموضع الارتكاز من ناحية، يتوجب علينا مضاعفة الحمل من الناحية الأخرى حتى نصل لحالة التوازن كما يلي:
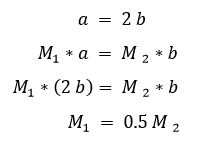
وهذا المثال يقتصر على الأوزان الموضوعة على الرافعة، لكن يمكن استبدال هذه الأوزان بأي شكل من أشكال القوى مثل القوة التي تبذلها ذراع إنسان على الرافعة. ومن هنا تظهر أهمية الرافعة. إذا كنت ترغب في تثبيت وزن مقداره 1000 رطل على سبيل المثال، يمكنك حمله بواسطة قوة مقدارها 500 رطل فقط عن طريق مضاعفة المسافة من جهة القوة الداخلة. وإذا كانت المسافة من جهة القوة الداخلة تساوي أربع أمثال المسافة من الناحية الأخرى، يمكن تثبيت هذا الحمل بواسطة قوة مقدارها 250 رطلًا فقط، وهلم جرًا.
أصناف الروافع
في حالة استخدام الروافع لبذل الشغل (أي لتحريك الأجسام)، فإننا نركز فقط على نقل القوة الداخلة التي نتحكم بها إلى القوة الخارجة التي تؤثر على الحمل من الناحية الأخرى. فعلى سبيل المثال، حين تستخدم العتلة حتى تنزع مسمارًا، فأنت تؤثر بذراعك بقوة داخلة لتحرير المسمار بقوة خارجة، والتي تنزع المسمار من مكانه.
وبوسعنا إعادة بناء وترتيب أجزاء الرافعة لتكوين ثلاثة أصناف أساسية من الروافع:
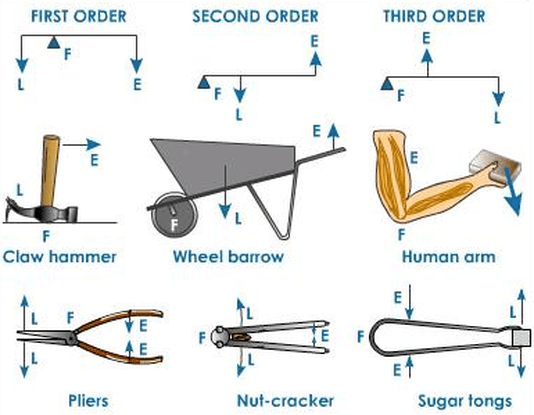
- رافعة من الرتبة الأولى: وهي تشبه الميزان الذي تحدثنا عنه مسبقًا؛ نقطة الارتكاز في المنتصف، والأحمال على الطرفين. مثال: العتلة، الزرادية.
- رافعة من الرتبة الثانية: وفيها يتواجد الحمل في المنتصف بين القوة المؤثرة ونقطة الارتكاز. مثال: عربة اليد ذات العجلة الواحدة، كسارة البندق.
- رافعة من الرتب الثالثة: وفيه تكون نقطة الارتكاز على جانب، والحمل على جانب آخر، بينما القوة المؤثرة في المنتصف. مثال: الملقاط، الذراع البشرية.
كل شكل من هذه الأشكال تولد منفعة آلية بطريقة أو بأخرى. وحتى تتضح فكرة المنفعة الآلية أكثر علينا أن نفهم قانون الروافع الذي أدركه أرشميدس مسبقًا.
قانون الروافع
المبدأ الرئيسي للروافع هو أن النسب بين المسافات من نقطة الارتكاز تحدد العلاقة بين القوى الداخلة والخارجة. إذا قمنا بتعميم المعادلة السابقة الخاصة بتوازن الكتل على الرافعة واستبدلنا الأوزان بقوة داخلة Fin وقوة خارجة Fout، نحصل على معادلة توضح لنا أن مجموع العزوم المؤثرة على الرافعة ثابتة:
![]()
بوسعنا الآن صياغة معادلة لحساب المنفعة الآلية علمًا بأنها النسبة بين القوة الخارجة إلى القوة الداخلة:
![]()
في المثال السابق، إذا كانت a = 2b فإن المنفعة الآلية تساوي 2، مما يعني أنه يمكن حفظ توازن حمل مقداره 1000 رطلًا باستخدام قوة مبذولة مقدارها 500 رطلًا فقط.
في الروافع من النوع الأول، يمكن تغيير قيمة المنفعة الآلية إلى مجال لا محدود من القيم عن طريق التلاعب بأي متغير كما يحلو لنا. أما الروافع من النوع الثاني والثالث تحتم وجود بعض القيود أمامنا.
في حالة الرافعة من النوع الثاني، فإن الحمل يتواجد في المنتصف، مما يعني أن a أكبر من b في جميع الأحوال. وبالتالي فإن المنفعة الآلية في النوع الثاني دائمًا ما تكون أكبر من الواحد، حيث أن هذه الروافع تستعمل في رفع الأحمال الثقيلة بسهولة أو توليد قوة هائلة لكسر شئ ما.
أما في حالة الرافعة من النوع الثالث، فإن القوة المبذولة تتواجد في المنتصف، مما يعني أن b اكبر من a دائمًا وأن المنفعة الآلية دائمًا ما تكون أصغر من الواحد. وتجدر الإشارة أن هذا النوع من الروافع لا نقصد به رفع الأحمال الثقيلة، بل نريد به أن نقلل القوة الخارجة حتى لا تحطم الأجسام التي ننوي تحريكها، ونركز على توليد قوة احتكاك كافية للإمساك بهذا الجسم، كما هو الحال في الملقاط الذي نحتاجه عادة للإمساك بالأشياء الصغيرة والتي قد تكون قابلة للتحطم بسهولة.
الرافعة في الحياة الواقعية
هذه المعادلة تعبر عن نموذج مثالي للرافعة. فقد قمنا بفرض بعض الفروض والتي قد تغير تمامًا النتائج التي نحصل عليها في الحياة الواقعية:
- أن الكمرة مستقيمة وجامدة تمامًا لا تنحني.
- أنه لا تتولد أي قوة احتكاك بين الكمرة ونقطة الارتكاز.
حتى في أحسن الأحوال، فقد نحصل على نتائج تقريبية فقط. فلا يمكن صناعة نقطة ارتكاز بلا أي قوة احتكاك.
أما الاحتمال الثاني فهو على الأرجح يتسبب في مشاكل أكثر من سابقه.
عساك تتذكر المثال السابق حيث قمنا باستخدام وزنًا مقداره 250 رطلًا حتى يعادل 1000 رطلًا. وفي هذه الحالة يجب على الكمرة أن تتحمل كلتا هاتين القوتين بدون أن تتقوس أو أن تنكسر. ونعتمد في هذه الحالة على نوع المادة لتحديد ما إذا كان هذا الفرض منطقيًا أم لا.
العجلة وعمود الدوران
العجلة هي أداة مستديرة متصلة بعمود صلب في مركزها. عند التأثير عليها بواسطة قوة فإنها تبدأ بالدوران وكذلك عمود الدوران بدوره، وبوسعنا استغلال هذا التصميم في مضاعفة هذه القوة (على سبيل المثال، عن طريق لف حبل حول عمود الدوران). يمكن تمثيل هذا النظام على أنه رافعة تدور حول محور ارتكاز في مركز العجلة. وتعتبر الساقية والإطارات والنشابة أمثلة على هذه الآلة.

مبدأ العمل
تستخدم العجلة بشكل مشابه جدًا للرافعة التقليدية، إلا أننا قمنا باستبدال الكمرات بعجلات مستديرة مثبتة تمامًا عن طريق محور ارتكاز. مما يعني أنه يمكن نقل القوة إلى مستوى آخر على طول المحور. بالإضافة إلى أنه يمكننا تقليل الإحتكاك بين العجلة ومحور الارتكاز عن طريق استخدام حامل كرات معدنية (رولمان بلي)، حيث أن مقاومة الكرات للدحرجة (rolling resistance) هي أقل بكثير من المقاومة بين الأسطح الخشنة.
ولا يزال قانون الروافع قائمًا في هذه الحالة. فقط علينا أن نستبدل المسافات بين نقطة الإرتكاز بنصف قطر العجلة ونصف قطر محور الدوران كما يلي:
![]()
والمنفعة الآلية:
![]()
ويمكن إضافة عجلة أخرى ذات نصف قطر أصغر على طول المحور عوضًا عن استخدام العمود ذات نفسه. وبدلًا من استخدام الحبال، يمكن استخدام تروسًا (gears) أو سلاسل وعجلات ذات أسنان (chain and sprocket wheel) أو السيور.
الأسطح المائلة
السطح المائل هو سطح مثبت بزاوية معينة بينه وبين السطح الأفقي. مما يتيح لنا أن نبذل نفس مقدار الشغل بقوة أقل على مسافة أطول. ومن أبسط أنواع الأسطح المائلة هو السطح المنحدر؛ حيث أنه من الأسهل الصعود أعلى سطح منحدر على أن تتسلق أرضًا مرتفعة بشكل عمودي مباشرة. ويعتبر الإسفين أو الخابور عادة نوعًا خاصًا من الأسطح المائلة.
قانون السطح المائل بسيط للغاية. نحن نعرف من خلال حساب المثلثات أنه يمكن تحليل أي متجه إلى مركبتين عمودتين. عند تسلق منحدر معين فأنت تبذل شغلًا ضد مركبة الوزن المائلة في اتجاه المستوى المائل على المستوى الأفقي. ويتضح من الصورة المرفقة بالأسفل أن هذه القوة تتعين من خلال العلاقة:
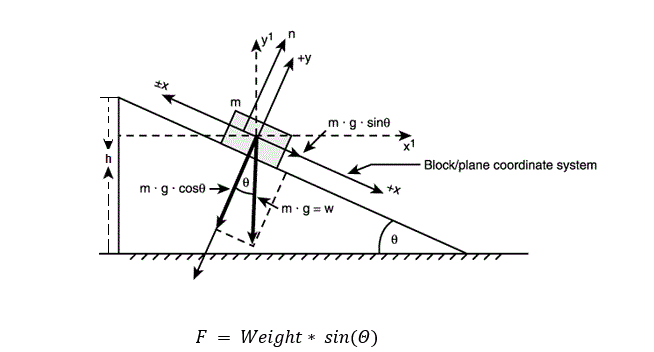
حيث أن Θ هي الزاوية بين المستوى المائل والأفقي
وحتى نتأكد من عدم اختراق قانون حفظ الطاقة، دعنا نقوم بحساب الشغل المبذول على السطح المائل:
![]()
وهو نفس الشغل المبذول ما إذا قررت الصعود عموديًا.
وبالتالي فإن المنفعة الآلية:
![]()
وفي العالم الواقعي عليك أن تتغلب على قوة الاحتكاك بين السطح المائل والشئ الذي تحركه، مما يعني أن الكفائة تظل أقل من الواحد (وهذه نتيجة حتمية لقانون الديناميكة الحرارية الثاني).
الإسفين أو الخابور
هو سطح مائل مزدوج (مما يعني أن كلا من جانبيه مائل على المستوى الأفقي) نقوم بتحريكه حتى يؤثر بقوى عمودية على طول جانبيه بغرض إزاحة جسمين عن بعضهما (أو فصل جزئين من جسم واحد عن بعضهما). في العادة يكون الإسفين قطعة من الخشب أو المعدن سميكة من أحد الأطراف ويقل سمكها حتى تصبح حادة من الطرف الآخر. وهي تستخدم في قطع الأخشاب، ورفع الأثقال الكبيرة، وكدعامة لبعض المنشئات…إلخ.
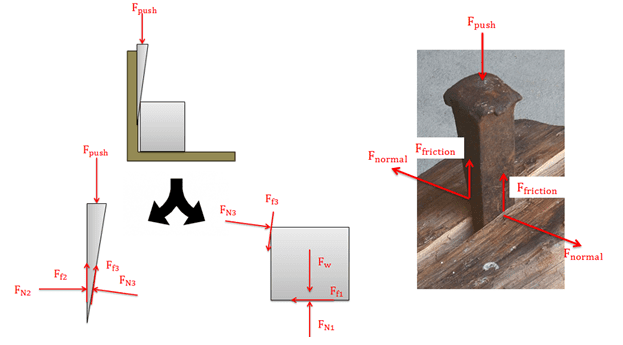
تعتمد فكرة الإسفين على العلاقة بين قوة الإحتكاك بين سطحين والقوة العمودية المؤثرة على السطح. وتلك هي العلاقة الشهيرة التي تربط بينهما:
![]()
حيث أن قيمة الثابت µ في العادة أصغر بكثير من الواحد الصحيح. وبذلك تكون النسبة بين القوة العمودية إلى قوة الاحتكاك كبيرة جدًا. وذلك يعني أن القوة المؤثرة على الإسفين ينتج عنها قوة كبيرة جدًا تؤثر على الجسم المراد تحريكه أو فصله أو رفعه.
وفكرة عمل الإسفين مشابهة إلى حد كبير لفكرة عمل السطح المائل، حيث أنه يجب تحريك الإسفين لمسافة طويلة من أجل إزاحة الجسم لمسافة قصيرة نسبيًا إذا ما قورنت بالمسافة التي يتحركها الإسفين. وتؤثر قوى الاحتكاك كالعادة على كفاءة الإسفين.
وبالتالي يمكن التعبير عن المنفعة الآلية في الحالة المثالية بالمعادلة الآتية:
M.A. = L/t
حيث L هو طول الإسفين، و t هو أكبر سمك للإسفين.
البرغي أو القلاووظ
البرغي هو عمود عليه مجرى مائل على طول محوره. وبالنظر إلى البرغي من منظور أفقي يبدو وكأن له عدة أسنان يفصل بين كل منها مسافة صغيرة جدًا. وعندما تقوم بتدوير البرغي دورة كاملة داخل فتحة ربط البرغي، فإن البرغي يتحرك حركة خطية مقدارها الفاصل بين كل سن لأسفل أو لأعلى على حسب إتجاه العزم المؤثر عليه. يستخدم بكثرة في ربط الأشياء ببعضها (مثال: البرغي والصمولة في تثبيت الأجزاء الصلبة في المعدات الثقيلة والأجهزة الكهربائية.)
والمنفعة الآلية في هذه الحالة هي النسبة بين محيط البرغي وطول الفاصل بين الأسنان. إلا أن المنفعة الآلية بمفهومها الحالي ليس لها أهمية كبيرة حيث أنه تتولد قوة احتكاك كبيرة تؤثر سلبًا وبشكل ملحوظ على المنفعة الآلية.
البكرات
البكرة هي عجلة لها مجرى صغير على طول محيطها، حيث يوضع في مكانه حبلًا أو كابل. تعتمد فكرة البكرة الواحدة على تأثير قوة صغيرة خلال مسافة كبيرة لرفع الأجسام الثقيلة، وبالتالي تعريف المنفعة الآلية هنا لا يختلف كثيرًا عن حالة المستوى المائل. ويمكن باستخدام البكرة نقل اتجاه القوة إلى أي اتجاه آخر في مستواها.
ويمكن استخدام نظام معقد يتكون من عدة بكرات كما بالشكل بالأسفل. يمكن لمثل هذه الأنظمة أن تقلل قيمة القوة المطلوبة لرفع جسم ما عن طريق توزيع قوى الشد على عدة بكرات باستخدام حبل أو سير أو أي آلية أخرى مشابهة. وذلك بالطبع يكون على حساب المسافة التي يصعدها الحمل.
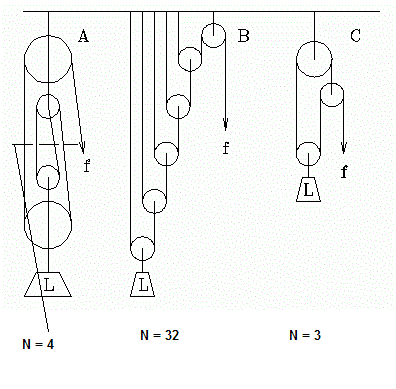
حيث أن المنفعة الآلية:
M.A. = N
تلك كانت الآلات الست البسيطة كما تم تصنيفها وتعريفها بواسطة علماء عصر النهضة في أوروبا. ولك أن تتخيل كيف شكلت هذه الأدوات البسيطة حياة البشر منذ فترة ازدهار اليونانيين القدماء وحتى ما قبل عصر الثورة الصناعية واكتشاف الوقود. لا شك أن كان لها جل الأهمية في تسريع تطور الحضارات البشرية وبالأخص الحضارات الغربية منذ عصر اليونان القديمة مرورًا بالعصور الوسطى وانتهاءًا بالعصر الحديث.
المصادر
ترجمة وإعداد: حازم موسى
مراجعة: أحمد رضا
تحرير: زياد الشامي

