
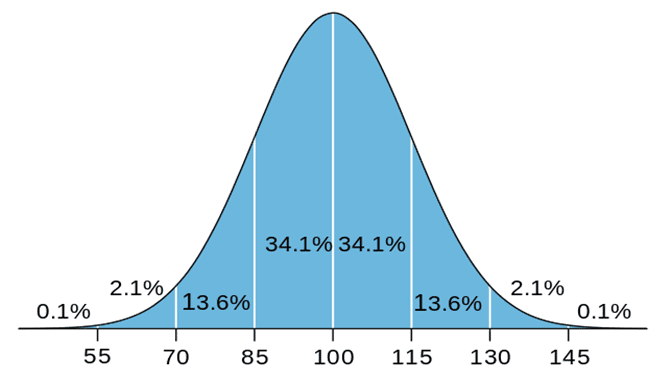
« نسبة الذكاء ـ intelligence quotient» او ما يعرف بال IQ هو نتيجة مجموعة من الاختبارات التي تهدف لتحديد الذكاء الانساني، اطلق هذا المصطلح العالم الالماني ( ويليام ستيرن – William Stern) عام 1912، بعد اجراء العديد من الاختبارات وجد ان متوسط درجة الذكاء هي 100 و وجد ان الانحراف المعياري لهذة الدرجة هو 15 درجة اعلي او اقل من المتوسط .
الصورة التالية توضح نسبة الذكاء بالنسبة للمجتمع
هناك العديد من المواقع التي يمكن قياس نسبة الذكاء عن طريقها، هناك العديد من الجمعيات المهتمه بك اذا كان معدل ذكائك مرتفع مثل :
يمكنك الانضمام اذا كنت من اذكى 2% في المجتمع .
لسنا بصدد التعرض للمزيد من التفاصيل المتعلقة بالأصول التاريخية لنسبة الذكاء، أهم جزء نريد أن نتعرض له هو أن اختبارات الذكاء تعتمد في الاساس علي الذكاء الرياضي ( الجبري و الهندسي ) و المنطقي .
لذلك في هذة السلسلة سنبدأ في تحليل تلك الاسئلة و إيجاد العلاقات و الطرق الرياضية لحلها و سنبدأ هذة المرة بالمتسلسلات العددية, بالطبع هو مجال واسع في حد ذاته لذلك يمكن ان نتطرق الية في مرة اخري
الفكرة الرئيسية في المتسلسلات العددية هو وجود مجموعة من الارقام يوجد بينهم رابط معين مع وجود رقم ناقص
قبل أن نبدأ في الطرق يمكنك ان تحاول ان تحل اللألغاز القادمة :
1- 0, 1, 4, 9, 16, 25, 36, 49, ?
2- 9, 18, 27, ?, 45, ?, 63
3- 100, 96.75 , 93.5 , 90.25 , 87 , ?
4- 0, 100, 6, 94, 12, 88, 18, 82, ?, ?
5- 1, 1, 2, ?, 24, 120, 720
6- 100, 98, 94, 88, 80, 70, ?
7- 100, 50, 200, 25, 400, ?
8- 5, 26, 131, 656, ?
9- 1, 1, 3, 15, 105, ?
10- 1, 2, 6, 12, 36, 72, 216, ?, ?
والان سنبدأ في حل الأسئله و ايجاد طرق مجدية لتطبيقها علي أي اسئلة اخري، و في نهاية المقال سنقوم بتجميع كل الاساليب حتي يمكنك اللجوء لها فيما بعد
نبدأ بالسؤال الاول :
1- 0, 1, 4, 9, 16, 25, 36, 49, ?
هذا النوع من الاسئلة هو الابسط لانه يعتمد علي ابسط العمليات الحسابية و هي الجمع، لمعرفة اذا كانت هناك علاقة تعتمد علي الجمع بين ارقام السلسلة سنطرح كل رقم من الرقم السابق له
1-0 = 1
4- 1 = 3
9-4 = 5
16- 9 = 7
25-16 = 9
36- 25 = 11
مما سبق نجد ان الفرق بين كل رقم و ما يليه هو اضافة الارقام الفردية بالترتيب، اضافة 1 ثم 3 ثم 5 … الخ
و لكن هل هذة هي الطريقة الوحيدة ؟
هناك طريقة اخري تبدوا معقدة للوهله الاولي و هي ايجاد الجذر التربيعي للأرقم بالترتيب
لنجد العلاقة التالية
| 0 | 1 | 4 | 9 | 16 | 25 | 36 | 49 |
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
اذا العلاقة هذة المرة هي ايجاد تربيع الارقام بالترتيب، بما ان اخر رقم وجدنا تربيعه هو 7 ، فالرقم التالي هو 8 تربيع = 64
السؤال الثاني
2- 9, 18, 27, ?, 45, ?, 63
قد يبدوا هذا السؤال مختلف و لكن اذا امعننا النظر سنجد نفس الطريقة و هي علاقة الجمع
18-9= 9
27-9 = 9
حسناً قد يبدوا هذا مشجعاً و لكنه ليس كافياً، لا يمكن الاعتماد علي رقمين فقط للتأكد، لقد وجدنا ان العلاقة هي اضافة 9 في كل مرة اذا طبقنا هذا سنجد ان الارقام الناقصة هي
27 + 9 = 36
و 45+ 9 = 54
للتأكد من صحة الارقام
| 63 | 54 | 45 | 36 | 27 | 18 | 9 |
| 63-54=9 | 54-45= 9 | 45-36=9 | 36-27=9 | 27-18=9 | 18-9=9 |
العلاقة سليمة حيث الفرق بين كل رقم هو 9
السؤال الثالث
3- 100, 96.75, 93.5, 90.25, 87, ?
لوجود كسور قد يبدوا السؤال اصعب و لكن التطبيق سهل بالفعل، الارقام تتناقص اذا بديل الجمع هنا هو الطرح
| 100 | 96.75 | 93.5 | 90.25 | 87 |
| 100-96.75 =3.25 | 96.75-93.5 = 3.25 | الفرق 3.25 | الفرق 3.25 |
اذا الرقم التالي هو 87- 3.25 = 83.75
السؤال الرابع
4- 0, 100, 6, 94, 12, 88, 18, 82, ?, ?
هنا تبدأ الامور في ان تصبح اصعب قليلاً، الارقام تزيد ثم تقل ثم تعود لتزيد، لا يبدوا انها في سلسله منتظمة، و هذا حقيقي، في هذا المثال يوجد سلسلتين من الارقام الاولي تحتوي علي الارقام ( الاول، الثالث، الخامس… الخ) و الثانية هي ( الثاني ، الرابع، السادس… الخ )
سنقوم بفصل المجموعتين لنجد ان الاول هي
0, 6,12,18, ?
و الثانية
100,94,88,82,?
كما تعلمنا فيما سبق الاول هي جمع 6 و الثانية هي طرح 6
الارقام الناقصة هي 18+ 6 = 24
82- 6 = 76
السؤال الخامس
5- 1, 1, 2, ?, 24, 120, 720
الارقام تتزايد و لكن بتسارع شديد اذا العلاقة من الصعب ان تكون جمعاً، امامنا علاقة اخري هي الضرب، لمعرفة اذا كانت العلاقة صحيحة نقوم بقسمة كل رقم علي الرقم السابق له
| A | 1 | 1 | 2 | 24 | 120 | 720 | |
| A/السابقة A | 1 | 2 | ? | ? | 5 | 6 |
من الجدول السابق سنجد ان بقسمة الرقم علي الرقم السابق ينتجد ارقام تبدأ من رقم 1 و تزيد بمقدار 1 في المرة بمعني اخر، العلاقة هي ضرب اول رقم ف 1 ثم الناتج في 2 ثم الناتج في 3 ، بتطبيق الفرضية نجد التالي
| A | 1 | 1 | 2 | 6 | 24 | 120 | 720 |
| A/السابقة A | 1 | 2 | 3 | 4 | 5 | 6 |
اذا الفرضية سليمة
السؤال السادس
6- 100, 98, 94, 88, 80, 70, ?
الارقام تنقص بتسارع بسيط، افضل الاحتمالات هو الطرح، بتجربة الفرضية
| A | 100 | 98 | 94 | 88 | 80 | 70 | |
| Aالسابقة-A | 2 | 4 | 6 | 8 | 10 |
العلاقة هي طرح و لكن الارقم التي تطرح تزيد بمقدار 2 في المرة اذا الرقم الناقص هو 70 – 12 = 58
السؤال السابع
7- 100, 50, 200, 25, 400, ?
كما ذكرنا من قبل، الارقام تزيد ثم تنقص ثم تزيد يوحي بوجود سلسلتين داخل بعض، يمكن بوضوح ملاحظة ان الاولي 100، 200، 400 هي ناتج الضرب في 2، و 50، 25 هي نتيجة القسمة علي 2
اذا الناتج 25/2 = 12.5
السؤال الثامن
8- 5, 26, 131, 656, ?
هذا السؤال مختلف قليلاً اذا نظرنا للجمع سنجد التالي
| 656 | 131 | 26 | 5 | A |
| 525 | 105 | 21 | A – Aالسابقة |
لا توجد علاقة واضحة، لذلك يمكن تجربة شئ اخر هو الضرب
| 656 | 131 | 26 | 5 | A |
| 5.007 | 5.0384 | 5.2 | A / Aالسابقة |
هنا نجد ان العلاقة تقترب من الضرب في 5 و لكن ليس تماماً، هنا يجب الجمع بين الطريقتين ، الجمع و الضرب، سنبدأ بالضرب في 5
5*5 = 25
نجد ان الناتج سيصبح صحيح بأضافة 1
25+ 1 = 26
للتأكد سنطبق النظرية علي الباقي
26*5 = 130 + 1 = 131
131*5 = 655+ 1 = 656
اذا الرقم التالي هو
656 * 5 =3281
السؤال التاسع
9- 1, 1, 3, 15, 105, ?
العلاقة هو زيادة بتسارع شديد لذلك بتجربة الضرب
| 105 | 15 | 3 | 1 | 1 | A |
| 7 | 5 | 3 | 1 | A / Aالسابقة |
العلاقة هي ضرب الرقم * الارقام الفردية بالترتيب
اذا الرقم القادم هو 105 * 9= 945
السؤال العاشر
10- 1, 2, 6, 12, 36, 72, 216, ?, ?
العلاقة هو زيادة بتسارع شديد لذلك بتجربة الضرب
| 216 | 72 | 36 | 12 | 6 | 2 | 1 | A |
| 3 | 2 | 3 | 2 | 3 | 2 | A / Aالسابقة |
العلاقة هي ضرب الارقام في 2 ثم في 3
اذا الرقم التالي هو 216 * 2 = 432
في النهاية يمكن تجميع الطرق عند محاولة حل متتالية في الخطوات التالية
- ابحث عن الارقام اذا كانت في تزايد جرب علاقة الجمع او الضرب و كلاهما معا
- اذا كانت في تناقص ابحث في القسمة او الطرح او كلاهما معاً
- التسارع الشديد في زيادة او نقصان الارقام من الممكن ان يكون جذر او أس
- اذا لم يكن واضح زيادة او نقصان فأن من الممكن وجود سلسلتين متداخلتين في نفس الوقت
إعداد : مينا نسيم
مراجعة علمية : Ahmed Hosiny

