
الهندسة التفاضلية
قصة الساحرة المستترة
الجزء الأول
مبادئ نظرية المنحنيات
د. علي فرحات
- قلَّما نجد فرعًا من فروع المعرفة يلعب دورًا بأهمية وانتشار وتأثير الهندسة التفاضلية، ليس فقط على الرياضيات، بل على علوم كالفيزياء النظرية وهندسة التحكم. بالإضافة إلى ذلك، يؤثر تطور الهندسة التفاضلية على تشكيل فهمنا لأعماق الرياضيات وسبر أغوارها عن طريق كشف علاقات لم تكن معروفة بين الصيغ الحسابية للدوال التحليلية ومقابلها الهندسي في الفراغات الرياضية.
في الجزء الأول من سلسلة مقالات الهندسة التفاضلية، نرفع الستار عن ذلك الفرع المهم من الرياضيات فنعرض لماهيته، نشأته، مكوناته ثم نعرض بشيء من التفصيل مبادئ نظرية المنحنيات ثلاثية الأبعاد.
-
ما هي الهندسة التفاضلية؟
كما يُستشف من العنوان، الهندسة التفاضلية هي دراسة الخصائص المحلية والشاملة للمنحنيات والسطوح في الفراغات الرياضية؛ بتطبيق مبادئ التحليل الرياضي -أي التفاضل والتكامل- عليها. يمكن ملاحظة بعض إرهاصات أو بدايات للهندسة التفاضلية في أعمال نيوتن عند وضعه مبادئ حساب التفاضل والتكامل في القرن السابع عشر. فقيمة تفاضل دالة حقيقية في متغير حقيقي عند النقطة (س) هي ميل المماس لمنحنى الدالة عند (س). كما أنَّ قيمة تكامل منحنى دالة من النقطة (أ) إلي النقطة (ب) هي المساحة المحصورة تحت منحنى الدالة مع محور المتغير المستقل للدالة. ولكن هل تقتصر الهندسة التفاضلية على إضفاء معنى هندسي للعمليات التحليلية على الدوال الحقيقية؟
-
النشأة والتاريخ
الأسئلة المُلحة التي ساهمت في بداية الهندسة التفاضلية:
- هل هناك صيغ رياضية عامة لحساب الأطوال والمساحات والأحجام المتضمنة لمجموعة عامة من المنحنيات والسطوح في الفراغ ثلاثي الأبعاد؟
- هل هناك صيغ رياضية عامة لحساب خصائص المنحنيات والسطوح تتحقق صحتها بغض النظر عن اختيارنا لإحداثيات تمثل تلك العناصر الهندسية؟
- هل يمكننا تعميم تلك الصيغ لدراسة الدوال الملساء ومجالات المتجهات، أو عناصر رياضية أعم معرفة على تلك المنحنيات أو السطوح ذات الخصائص العامة؟
- هل يمكننا تعميم تلك الصيغ الرياضية لفراغات ذات أكثر من ثلاثة أبعاد، أو حتى لا نهائية الأبعاد؟
- ما هي العناصر أو المكونات التحليلية لوصف وتحديد فراغات أو أسطح عامة، غير إقليدية بالضرورة، وذات أكثر من ثلاثة أبعاد؟
نشأت تلك الأسئلة واحدًا تلو الآخر في فترات زمنية متباعدة وظروف مختلفة، لكنَّها صبَّت كلها نحو فهم أعمق للخصائص الهندسية المحلية والشاملة للفراغات الرياضية، وما صحبها من فهم أعمق وأشمل لهندسة الكون المؤسِّسة لنطريات، كنظرية ميكانيكا لاجرانج وهاملتن والنسبية العامة.
ظهرت المقدمات الأولى للهندسة التفاضلية في أعمال أيلر(Leonhard Euler) ومونجي(Gaspard Monge) في القرن الثامن عشر. وكان أول تناول مفصل لنظرية الأسطح على يد مونجي في كتابه (Une application d’analyse à la géométrie, 1795) تطبيق للتحليل الرياضي على الهندسة. عام 1827م، نشر جاوس(Carl Friedrich Gauss) دراسته المشهورة تحت عنوان مترجم بالإنجليزية ل(A general study on curved surfaces)دراسةً عامةً عن الأسطح المنحنية والتي أسَّست لنظرية الأسطح في شكلها الحالي. منذ ذلك الوقت، أصبحت الهندسة التفاضلية فرعًا مستقلًا من أفرع الرياضيات بعد أن كانت مجرد تطبيقًا للتحليل الرياضي.
كان لاكتشاف لوبشيفسكي(Nikolai Lobachevsky) عام 1826م للهندسة غير الإقليدية دورًا كبيرًا في تطور الهندسة ككل، بما في ذلك الهندسة التفاضلية. فقد رفض لوبشيفسكي المفاهيم التقليدية عن الفراغ والتي كانت متبنَّاه آنذاك في الرياضيات والفلسفة. فقد أثبت وجود فراغات مختلفة عن تلك التي أسس لها إقليدس منذ ألفي عام. انعكست أفكار لوبشيفسكي على كثير من الدراسات الرياضية ممَّا دفع برنارد ريمان(Bernhard Riemann) عام 1854م لنشر عمله (Über die Hypothesen, welche der Geometrie zuGrunde liegen) عن الفرضيات المؤسسة للهندسة، والذي وضع الأساس لِما يُعرف بالهندسة الريمانية نسبةً لمؤسسها. ويُعد تطبيق هندسة ريمان على الفراغات متعددة الأبعاد وعلاقتها بالفراغ الإقليدي متعدد الأبعاد مماثلًا لتطبيق المفاهيم الذاتية للأسطح كالانحناءات الرئيسية وعلاقتها بالمستوى الإقليدي.
بنهاية القرن التاسع عشر وبداية القرن العشرين، ساهم كل من فيليكس كلاين(Felix Klein) وإيلي كرتان(Élie Cartan) في دراسة جبرية مؤسسة على التحويلات بنظرية المجموعات (group-theoretic transformations) نحو فِهم الكميَّات الثابتة تحت تأثير تلك التحويلات الجبرية. -
مبادئ نظرية المنحنيات – الهندسة الخارجية – الهندسة الذاتية
كانت بدايات الهندسة التفاضلية بدراسة المنحنيات والأسطح الكائنة في الفراغ الإقليدي ثلاثي الأبعاد. يُسمى هذا النوع من الهندسة التفاضلية بالهندسة الخارجية نظرًا لضرورة وجود فضاء حاوٍ للعناصر الهندسية قيد الدراسة من منحنيات أو أسطح.
نفترض من الآن أنَّ موضوعات مثل الجبر الاتجاهي وأساسيات التحليل مألوفة بالنسبة للقارئ.
يُعرف أي منحنى كدالة متصلة وأحادية (homeomorphism)
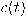 من مجموعة الأعداد الحقيقية لأي فراغ طوبولوجي، في حالة دراسة الهندسة الخارجية، نكتفي بأن تكون قيم الدالة في مجموعة
من مجموعة الأعداد الحقيقية لأي فراغ طوبولوجي، في حالة دراسة الهندسة الخارجية، نكتفي بأن تكون قيم الدالة في مجموعة 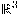 . ويُعرف المنحنى بدوال الموضع الكارتيزية أو متجه الموضع البرامتري
. ويُعرف المنحنى بدوال الموضع الكارتيزية أو متجه الموضع البرامتري 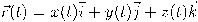 وهي إحداثيات نقطة ما على المنحنى في الفراغ الإقليدي ثلاثي الأبعاد. تتطلب شروط وجود المنحنى أن تكون هناك عند كل قيمة للمتغير
وهي إحداثيات نقطة ما على المنحنى في الفراغ الإقليدي ثلاثي الأبعاد. تتطلب شروط وجود المنحنى أن تكون هناك عند كل قيمة للمتغير 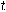
 مشتقة واحدة على الأقل من
مشتقة واحدة على الأقل من 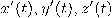 لا تتساوي مع الصفر حتى نضمن تعريف متجه مماس غير صفري عند كل نقطة على المنحنى، ويسمى ذلك الشرط بشرط الانتظام (Regularity Condition).
لا تتساوي مع الصفر حتى نضمن تعريف متجه مماس غير صفري عند كل نقطة على المنحنى، ويسمى ذلك الشرط بشرط الانتظام (Regularity Condition).جدير بالذكر أنَّ اختيار البرامتر
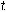
 ليس وحيدًا، بل هناك عدد لا نهائي من اختيارات البرامتر تحقق شروط تعريف دالة المنحنى c(t). أحد اختيارات البرامتر هو طول المنحنى s من نقطة بداية معلومة على المنحنى
ليس وحيدًا، بل هناك عدد لا نهائي من اختيارات البرامتر تحقق شروط تعريف دالة المنحنى c(t). أحد اختيارات البرامتر هو طول المنحنى s من نقطة بداية معلومة على المنحنى 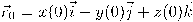 بحيث تكون الدالة البارامترية للمنحنى في صورة
بحيث تكون الدالة البارامترية للمنحنى في صورة 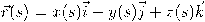 . جدير بالذكر أنَّ العلاقة التفاضلية ما بين طول المنحنى وتعريفه الكرتيزي هي
. جدير بالذكر أنَّ العلاقة التفاضلية ما بين طول المنحنى وتعريفه الكرتيزي هي 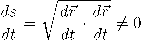 ، وبالتالي نستنتج أنَّ الدالة ((s(t) أحادية ومتصلة (homemorphism) في جوار النقطة t من قانون مقلوب الدالة (Inverse Function Theorem).
، وبالتالي نستنتج أنَّ الدالة ((s(t) أحادية ومتصلة (homemorphism) في جوار النقطة t من قانون مقلوب الدالة (Inverse Function Theorem). -
المماس – العمودي – المستوى الملاصق عند نقطة على المنحنى
يُعرف المتجه المماس
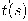 للمنحنى البارمتري
للمنحنى البارمتري 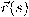 بالمعادلة
بالمعادلة 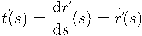 . يمكننا بسهولة ملاحظة أنَّ المتجه المماس طوله وحدة واحدة بسبب أن
. يمكننا بسهولة ملاحظة أنَّ المتجه المماس طوله وحدة واحدة بسبب أن 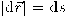 مما ينتج عنه أن
مما ينتج عنه أن 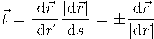 وهو متجه وحدة.
وهو متجه وحدة.إنَّ دراسة مفكوك تايلر لدالة الموضع على المنحنى يمكننا من تفهم كثير من الخصائص الهندسية-التحليلية للمنحنيات في
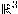 خصوصًا و
خصوصًا و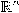 عمومًا وكذلك الإتيان بخصائص محليَّة للمنحنيات تمكننا من دراستها ذاتيًا، أي بعيدًا عن أي فراغ إقليدي حاوٍ. تحديدًا، يمكننا مفكوك تايلر من معرفة شكل المنحنى في جوار نقطة
عمومًا وكذلك الإتيان بخصائص محليَّة للمنحنيات تمكننا من دراستها ذاتيًا، أي بعيدًا عن أي فراغ إقليدي حاوٍ. تحديدًا، يمكننا مفكوك تايلر من معرفة شكل المنحنى في جوار نقطة 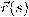 بمعلومية متجه المماس
بمعلومية متجه المماس 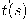 وجميع مشتقاته بالنسبة لطول المنحنى
وجميع مشتقاته بالنسبة لطول المنحنى  .
.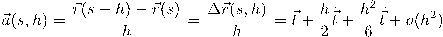
حيث إنَّ
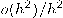 تئول للصفر عندما
تئول للصفر عندما 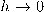 . على وجه الخصوص، في الفراغ الإقليدي ثلاثي الأبعاد عند النقطة
. على وجه الخصوص، في الفراغ الإقليدي ثلاثي الأبعاد عند النقطة 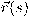 ، يمثل المتجه
، يمثل المتجه 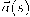 كتركيبة خطيَّة من ثلاثة متجهات مستقلة على الأكثر. وعليه، فإنِّ مهمتنا الآن هي إيجاد تمثيل المتجه المماس وجميع مشتقاته بدلالة ثلاثة متجهات أساس للفراغ الإقليدي الثلاثي المعرف عند النقطة
كتركيبة خطيَّة من ثلاثة متجهات مستقلة على الأكثر. وعليه، فإنِّ مهمتنا الآن هي إيجاد تمثيل المتجه المماس وجميع مشتقاته بدلالة ثلاثة متجهات أساس للفراغ الإقليدي الثلاثي المعرف عند النقطة 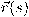 ،
، 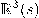 .
.نظرية 1:
إذا كانت
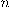
 هي أقل قيمة صحيحة حيث أنَّ المشتقة
هي أقل قيمة صحيحة حيث أنَّ المشتقة 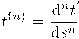 تركيبة خطية من المشتقات الأقل رتبة للمتجه المماس، فإن المتجه
تركيبة خطية من المشتقات الأقل رتبة للمتجه المماس، فإن المتجه 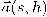 يمكن تمثيله في فراغ ذو
يمكن تمثيله في فراغ ذو 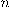 بعد.
بعد.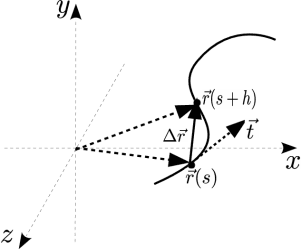 الإثبات: يمكن تمثيل المشتقة
الإثبات: يمكن تمثيل المشتقة 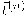 كتركيبة خطية من كل الرتب الأقل. بالاشتقاق مرة واحدة، تصبح
كتركيبة خطية من كل الرتب الأقل. بالاشتقاق مرة واحدة، تصبح 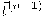 تركيبة خطية من المشتقات من الرتبة 0 إلى n على أن نعوض عن
تركيبة خطية من المشتقات من الرتبة 0 إلى n على أن نعوض عن 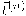 بتركيبتها الخطية، فتصبح
بتركيبتها الخطية، فتصبح 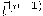 تركيبة خطية في المشتقات من الرتبة 0 إلى n-1. نفس التفكير يمكن تطبيقه على جميع المشتقات من رتب أعلى إلى ما لا نهاية. بالتعويض في مفكوك تايلر، يثبت أنَّ المنحنى يحتاج فقط للمتجه المماس وقيمة مشتقاته حتى الرتبة n-1 كي يعرف كلية. ومن هنا ينتج أن أقل بعد للفراغ الإقليدي الحاوي للمتجه
تركيبة خطية في المشتقات من الرتبة 0 إلى n-1. نفس التفكير يمكن تطبيقه على جميع المشتقات من رتب أعلى إلى ما لا نهاية. بالتعويض في مفكوك تايلر، يثبت أنَّ المنحنى يحتاج فقط للمتجه المماس وقيمة مشتقاته حتى الرتبة n-1 كي يعرف كلية. ومن هنا ينتج أن أقل بعد للفراغ الإقليدي الحاوي للمتجه 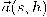 هو
هو 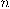 .
. 

ملاحظة: يمكن اختيار المتجه المماس ومشتقاته المستقلة كمتجهات الأساس للفراغ الحاوي للمتجه
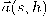 . ولكننا بحاجة إلى إطار وحدة متعامد(orthnormal reference frame) نُسميه إطار فرينيه ونختار متجهات أساسه كما يلي.
. ولكننا بحاجة إلى إطار وحدة متعامد(orthnormal reference frame) نُسميه إطار فرينيه ونختار متجهات أساسه كما يلي.نختار
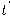
 كمتجه الأساس الأول. من اشتقاق العلاقة
كمتجه الأساس الأول. من اشتقاق العلاقة 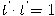 نستنتج أن
نستنتج أن 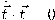 مما يعني أن المشتقة الأولى للمماس عمودية على المتجه المماس. ومن صيغة مفكوك تايلر، نرى أن المكون الأساسي للمتجه
مما يعني أن المشتقة الأولى للمماس عمودية على المتجه المماس. ومن صيغة مفكوك تايلر، نرى أن المكون الأساسي للمتجه 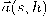 هو المتجه المماس.
هو المتجه المماس.ندرس المستوى
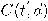 المكون من التركيبة الخطية للمتجه المماس والمتجه
المكون من التركيبة الخطية للمتجه المماس والمتجه 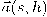 . من صيغة مفكوك تايلر، نلاحظ أن المتجه
. من صيغة مفكوك تايلر، نلاحظ أن المتجه 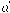
 يئول للتركيبة الخطية
يئول للتركيبة الخطية 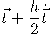 كلما صغرت قيمة
كلما صغرت قيمة 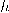
 . مستنتجين بذلك أن
. مستنتجين بذلك أن 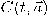 تئول للمستوى ذو الأساس الخطي المركب من من
تئول للمستوى ذو الأساس الخطي المركب من من 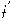 و
و 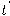 دون المشتقات الأعلى، وذلك بسبب إهمال الحدود الأعلى رتبة في مفكوك تايلر كلما اقترب المتجه
دون المشتقات الأعلى، وذلك بسبب إهمال الحدود الأعلى رتبة في مفكوك تايلر كلما اقترب المتجه 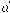 من المتجه
من المتجه 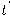 . يسمى المستوى المكون من أي تركيبة خطية للمتجه المماس ومشتقته الأولى عند النقطة
. يسمى المستوى المكون من أي تركيبة خطية للمتجه المماس ومشتقته الأولى عند النقطة 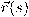 على المنحنى بالمستوى الملاصق (osculating plane) للمنحنى عند النقطة
على المنحنى بالمستوى الملاصق (osculating plane) للمنحنى عند النقطة 
 .
.نُعرف الانحناء الأول، أو دالة الانحناء
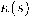 عند نقطة ما على المنحنى بأنَّها معدل دو ران المتجه المماس بالنسبة لتغير طول المنحنى، أو رياضيًا
عند نقطة ما على المنحنى بأنَّها معدل دو ران المتجه المماس بالنسبة لتغير طول المنحنى، أو رياضيًا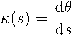 .
.وحيث إنَّ المتجه المماس هو متجه وحدة، أي أنَّ طوله وحدة واحدة لا تتغير، فإنَّ معدل دورانه يساوي قيمة معدل تغيره
.
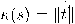
وعليه، نعرف متجه الوحدة العمودي
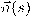 الواقع في المستوى الملاصق عند
الواقع في المستوى الملاصق عند 
 بالعلاقة
بالعلاقة 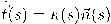 . ونختار
. ونختار 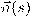 كمتجه الأساس الثان. ليكن متجه الأساس الثالث
كمتجه الأساس الثان. ليكن متجه الأساس الثالث 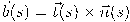 هو متجه الوحدة العمودي على السطح الملاصق للمنحنى عند
هو متجه الوحدة العمودي على السطح الملاصق للمنحنى عند  والمحسوب باستخدام الضرب الاتجاهي لمتجهي الأساس الأولين، بحيث تكون مجموعة متجهات الوحدة الأساسية
والمحسوب باستخدام الضرب الاتجاهي لمتجهي الأساس الأولين، بحيث تكون مجموعة متجهات الوحدة الأساسية 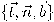 يمينية بالترتيب المذكور. جدير بالذكر أنه إذا كانت المشتقة الثانية للمماس معتمدة خطيًا على المشتقتين الأقل رتبة، فإنَّ المنحنى يمكن تمثيله كلية بالمتجه المماس ومشتقته الأولى، ومن ثم يصبح واقعًا في المستوى الملاصق، ويكون منحني مستويًا ليس بحاجة لفراغ حاوٍ ذي أكثر من بعدين اثنين.
يمينية بالترتيب المذكور. جدير بالذكر أنه إذا كانت المشتقة الثانية للمماس معتمدة خطيًا على المشتقتين الأقل رتبة، فإنَّ المنحنى يمكن تمثيله كلية بالمتجه المماس ومشتقته الأولى، ومن ثم يصبح واقعًا في المستوى الملاصق، ويكون منحني مستويًا ليس بحاجة لفراغ حاوٍ ذي أكثر من بعدين اثنين.يُسمى الإطار المعرَّف ب
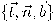 بإطار فرينيه للمنحنى
بإطار فرينيه للمنحنى 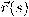 . وحتى يمكننا حساب المتجه
. وحتى يمكننا حساب المتجه 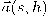 عن طريق المتجه
عن طريق المتجه 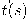 ومشتقاته، يجب علينا أولًا حساب مركبات المشتقة الأولى لمتجهات الأساس لإطار فرينيه. بمعلومية تلك المشتقات، يمكننا حساب مشتقة
ومشتقاته، يجب علينا أولًا حساب مركبات المشتقة الأولى لمتجهات الأساس لإطار فرينيه. بمعلومية تلك المشتقات، يمكننا حساب مشتقة 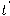 من أي درجة بدلالة متجهات الأساس لإطار فرينيه. بالفعل، لدينا أنَّ
من أي درجة بدلالة متجهات الأساس لإطار فرينيه. بالفعل، لدينا أنَّ 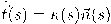 .
.لحساب مشتقة المتجه العمودي الواقع في المستوى الملاصق نستخدم:
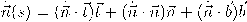
باستخدام
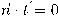 ، نستنتج أن:
، نستنتج أن:
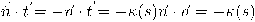 .
.باستخدام أن
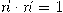 ، نستنتج أن
، نستنتج أن 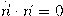 . ومن ثم تكون صيغة مشتقة الأساس العمودي الواقع في المستوى الملاصق عند
. ومن ثم تكون صيغة مشتقة الأساس العمودي الواقع في المستوى الملاصق عند  ،
،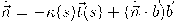
باستخدام أن
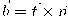 ، نستنتج من قاعدة اشتقاق حاصل ضرب الدوال أن:
، نستنتج من قاعدة اشتقاق حاصل ضرب الدوال أن:
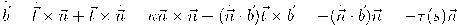
حيث إنَّ الكمية
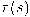 هي معدل دوران المستوى الملاصق عند
هي معدل دوران المستوى الملاصق عند 
 ويسمى بالالتواء (torsion) للمنحنى. نلاحظ أنَّ المستوى الملاصق يدور فقط حول العمودي وليس حول المتجه المماس.
ويسمى بالالتواء (torsion) للمنحنى. نلاحظ أنَّ المستوى الملاصق يدور فقط حول العمودي وليس حول المتجه المماس.مما سبق، يمكننا حساب الالتواء
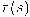 بدلالة المتجه المماس ومشتقاته كما يلي:
بدلالة المتجه المماس ومشتقاته كما يلي: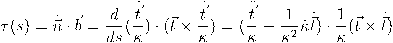
نلاحظ أنَّ الطرف الأيمن هو حاصل طرح ناتجي ضرب ثلاثي، ثانيهما صفر. بما أنَّ حاصل الضرب الاتجاهي هو متجه عمودي على كلا المتجهين المماس ومشتقته الأولى، فيكون حاصل الضرب الثلاثي المطروح قيمته صفر، ونخلص إلى أنَّ قيمة الالتواء بمعلومية المتجه المماس ومشتقاته تكون كالآتي:
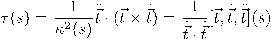
-
معادلات فرينيه – سيريه التفاضلية لإطار ثلاثي
من التحليل السابق، نحصل على معادلات إطار فرينيه لمنحنى ثلاثي الأبعاد، هي معادلات تصف أي منحنى بدلالة معطيات يمكن قياسها ذاتيًا. لنتخيل حشرة أو كائن يعيش على منحنى، هل يمكن لهذا الكائن قياس خصائص محليَّة عند كل نقطة للمنحنى بحيث يتمكن في النهاية من توصيف هذا المنحنى بشكلٍ كامل، أي الإتيان بالدالة البارمترية المنحنى بعد قياس تلك الخواص المحلية، وتمثيله بعد ذلك في أى فراغ حاوٍ. الخواص المحلية لأي منحنى فراغي هي الانحناء والالتواء. بمعرفة تلك القيم كدوال في طول المنحنى، مما سبق يمكننا حساب متجهات إطار فرينيه كالآتي:
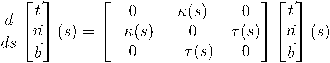 .
.معرفة هاتين الدالتين كافٍ لاستنتاج شكل المنحنى بسبب قانون وحدانية حلول المعادلات التفاضلية العادية. من ناحية أخرى، يمكن حساب كل مشتقات المتجه المماس بدلالة إطار فرينيه عند نقطة معينة، ومن ثمَّ استنتاج قيمة المتجه
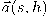 كمتسلسلة لانهائية من مفكوك تايلر عند
كمتسلسلة لانهائية من مفكوك تايلر عند 
 .
.مثال 1:
المنحنى الإهليجي مُعرَّف في الفراغ الإقليدي ثلاثي الأبعاد بالمعادلة البرامترية
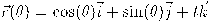 .
.نحسب أولًا المنحنى المماس كالآتي:
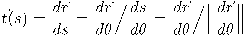
ولهذا نقوم بحساب مشتقة الدالة البرامترية للمنحنى بالنسبة ل
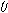

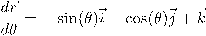
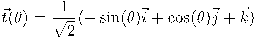
بطريقة مماثلة، نقوم بحساب المشتقة الأولى للمتجه المماس
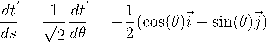
ونستنتج أنَّ الانحناء
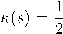 ثابت لا يتغير.
ثابت لا يتغير.لحساب الالتواء، نقوم أولًا بحساب المشتقة الثانية للمتجه المماس بطريقة مماثلة لحساب المشتقة الأولى:
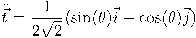
وأخيرًا لحساب الالتواء، نستخدم قانون الضرب الثلاثي والذي ينتج منه أنَّ
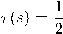 . نترك للقارئ تفاصيل الحساب كتمرين.
. نترك للقارئ تفاصيل الحساب كتمرين. -
خلاصة الجزء الأول
عرضنا بشكلٍ مختصر تاريخ الهندسة التفاضلية وظروف نشأتها. وعلمنا أنَّ الهندسة التفاضلية لها تأثير خفي لا يعرفه العامة في مجال الفيزياء النظرية وهندسة التحكم على الأخص، إلى جانب التطبيقات الحاسوبية في مجال الرسم بالحاسب وألعاب الواقع التخيلي.عرضنا بعد ذلك بشيء من التفصيل المبادئ التحليلية للمنحنيات في الفراغ الإقليدي العادي. ثم استنتجنا بعد ذلك أنَّ معرفة المتجه المماس ومشتقتيه الأولى والثانية كافٍ لاستنتاج المنحنى الفراغي باستخدام دالة مفكوك تايلر. اتجهنا بعد ذلك لحساب القيم الذاتية المميزة للمنحنى الفراغي والتي لا تعتمد على اختيارنا للفراغ الحاوِ أو أي نظام إحداثيات خارجي، واستنتجننا صيغ حسابية للانحناء والالتواء كأساس للمعادلات الطبيعية (الذاتية) لأي منحنى فراغي ثلاثي الأبعاد عن طريق المتجه المماس ومشتقتيه الأولى والثانية، انتهينا إلى معادلات فرينيه (سيريه) وهي معادلات تفاضلية تمكننا من حساب إطار وحدة متعامد عند كل نقطة في المنحنى الفراغي بمعرفة دالتي الالتواء والانحناء. أي، أنَّه بمعرفة متجهات إطار فرينيه عند نقطة ما على المنحنى بالنسبة لفراغ ثلاثي حاوٍ، وبمعرفة الانحناء والالتواء عند كل نقطة على المنحنى، يمكننا حساب شكل المنحنى في الفراغ الحاوِ عن طريق تكامل معادلات فرينيه (سيريه) التفاضلية.
في الجزء الثاني، نتبع نفس النهج لحساب المعادلات الطبيعية لمنحنيات في فراغ حاوِ ذو أكثر من ثلاثة أبعاد. نستنتج معادلات فرينيه (سيريه) للمنحنيات ذات عدد كبير من مشتقات المماس المستقلة خطيًا. نعطي بعد ذلك مقدمة عن نظرية الأسطح ثنائية الأبعاد ونتعرض أكثر لإسهامات جاوس في هذا المجال الخصب.
| إعداد | أ.د علي فرحات |
| تدقيق لغوي | أمنية أحمد عبد العليم |
| المصادر | Kreyszig, Erwin. Differential Geometry. Toronto: U of Toronto, 1959. Print.
Kühnel, Wolfgang. Differential Geometry: Curves – Surfaces – Manifolds. Providence, RI: American Mathematical Society, 2006. Print. السلمي، نصار حسن عبد العال. الهندسة التفاضلية. مكتبة الرشد، 2008. https://www.encyclopediaofmath.org/index.php/Differential_geometry |

