تحدثنا في الجزء الأول عن ماهية أشباه الموصلات، وذكرنا في لمحة بسيطة تطبيقاتها وأهميتها في كل جوانب أسلوب حياتنا المعاصرة، والتي صرنا نعتبرها الآن من المسلمات التي يشق علينا أن نستغني عنها. شرحنا أيضًا الأساس العلمي الذي تعتمد عليه أشباه الموصلات بأسلوب بسيط وغير تقني، وآخرًا ناقشنا أحد أبسط المكونات المصنعة منها وتطبيقاتها بالتفصيل الممل.

وفي هذا المقال أود أن أتبحر أكثر فيما يخص النظريات الفيزيائية التي تفسر عمل أشباه الموصلات، متسفيضًا في شرح النماذج والمعادلات الرياضية التي تحكمها. ومن ثم أود أن يتعرف القارئ على تطبيقات أكثر تعقيدًا من الدايود السابق ذكره، والتي فتحت المجال أمام عدد لا يحصى من الاختراعات والتطبيقات.

الدوائر الكهربية والدوائر الإلكترونية

بادئًا علينا الإجابة عن سؤال مهم جدًا: ما الفرق بين الدائرة الكهربية والدائرة الإلكترونية؟[1] في الحقيقة فإن مصطلح الدائرة الكهربية هو مصطلح عام يشمل جميع الأنظمة المغلقة التي تقوم بنقل وتحويل الطاقة الكهربية إلى صور أخرى والتلاعب بها، وهذا التعريف يشمل الدوائر الإلكترونية أيضًا حيث أنها تستمد طاقتها من الكهرباء.

أما الدوائر الإلكترونية فهي نوع خاص من الدوائر يحتوي على أجزاء ذات طبيعة خاصة. تعتبر الأجهزة المعتمدة على أشباه الموصلات من ضمن هذه الأجزاء. وهذه الأجزاء تسمى بالأجزاء الغير خطية والتي تتصرف بشكل مخالف لقانون أوم، أي أن العلاقة بين الجهد الكهربي بين طرفيها والتيار المار بها ليست علاقة خطية. تسمح هذه المكونات بأداء عمليات أكثر تعقيدًا من الأجزاء التقليدية مثل المقاومات والمكثفات. ومن أمثلتها: الدايود، الترانزستور، الصمامات الثلاثية، المكبر العملياتي (op-amp)، المعالج الحاسوبي المركزي…إلخ. ومن هذا المنطلق يمكننا أن نفرق بين نوعين من الدوائر اللإكترونية:

• الدوائر المنفصلة (discrete circuits): وهي دوائر تكون كل أجزائها على حدة، ويمكن فيها التعامل مع كل مكون بمفرده. وهي الدوائر التي يتصل فيها كل مكون بالآخر عن طريق أسلاك أو كابلات وليس عن طريق التلامس المباشر.
• الدوائر المتكاملة (integrated circuits): وهي في العادة عبارة عن رقاقات من مواد أشباه موصلة تضم أجزاء مختلفة عن طريق التلامس المباشر، وفي العادة لها عدة أطراف لأداء وظائف مختلفة. لا يمكن في هذه الحالة التعامل مع كل مكون بمفرده بل يجب التعامل مع تلك الرقاقة على أنها صندوق أسود يقوم ببعض العمليات بطريقة ما. يمكن أن تضم هذه الرقاقات داخلها دايودات، وترانزستورات، ومكثفات، وحتى كذلك مكونات حثية ذات قيم صغيرة (small inductions). ظهرت الحاجة لهذه الرقاقات كنتيجة حتمية لمشكلة تصغير الإلكترونيات والاقتصاد في استهلاك الطاقة، وهي مشكلات اقتصادية بحتة، بالإضافة إلى أن التعامل مع تلك الرقاقات أسهل بشكل فلكي من الدوائر المنفصلة. من أمثلتها: المكبرات العملياتية، البوابات المنطقية، معالجات الحواسيب، الذواكر الرقمية.[1]

انتقال الشحنات في أشباه الموصلات

توجد آليتان أساسيتان تتحكمان في مرور نواقل الشحنات عبر أشباه الموصلات[2]:

• تيار الإزاحة (Drift current): وهو حركة نواقل الشحنات نتيجة تأثير مجال كهربي على طرفي مادة شبه موصلة. فالمجال الكهربي ما هو إلا قوة تتسبب في تسارع الشحنات مولدًا ما يعرف بالجهد الكهربي، وهو فرق طاقة وضع بين نقطتين بسبب وجود مجال كهربي. ومن معرفتنا بقانون أوم المختص بالمواد الموصلة أن شدة التيار تتناسب طرديًا مع فرق الجهد الكهربي وعكسيًا مع مدى المعاوقة التي تعترض مسار الإكترونات.

وأشباه الموصلات تسلك سلوكًا مشابهًا بعض الشئ لسلوك الموصلات. ومن أهم الفروق التي نلاحظها أن تولد التيار الكهربي فيها قد يكون بسبب انتقال الإلكترونات أو الفجوات أو الاثنين معًا!

وقد تم إثبات العلاقة الطردية الآتية بين شدة المجال الكهربي وسرعة نواقل الشحنة معمليًا:

V = μ*E

حيث أن μ هو ثابت يسمى قابلية حركة الشحنات (charge mobility). وقيمة هذا الثابت في العادة تكون أكبر في حالة انتقال الإلكترونات من قيمة الثابت الخاص بانتقال الفجوات نظرًا لاختلاف الكتلة الفعلية للجسيمين. والعلاقة السابقة تظل صحيحة حتى تصل سرعة الجسيمات إلى سرعة الإشباع (saturation velocity) حيث الزيادة في شدة المجال لا تؤدي إلى زيادة إضافية في سرعة الجسيمات.

ومن خلال تلك العلاقة نستنتج علاقة أخرى وهي العلاقة بين المجال الكهربي وكثافة التيار في أشباه الموصلات:

J = (μn) *e*n*E + (μp) *e*p*E

يصف الحد الأول تيار الإلكترونات، والحد الثاني تيار الفجوات. حيث أن:

p هي كثافة الفجوات داخل البللورة.

nكثافة الإلكترونات.

e مقدار شحنة الإلكترون الواحد.

من تلك المعادلة نستنتج أن تياري الإلكترونات والفجوات، رغم أن اتجاههما متضادين، إلا أن شحنتيهما المتضادتين يولدان تيارًا كهربيًا في نفس الاتجاه بالظبط. وقد جرت العادة أن يكون اتجاه التيار الكهربي هو اتجاه سريان الشحنات الموجبة (الفجوات) أو عكس اتجاه سريان الشحنات السالبة (الإلكترونات).

• تيار الانتشار (Diffusion current): وتلك الآلية تعتمد على ظاهرة غير متعلقة على الإطلاق بالآلية السابقة، وتلك نلاحظها في حياتنا كل يوم. وكمثال راقب سقوط نقطة حبر في كوب من الماء، سوف تلاحظ أن الحبر قد انتشر من موقع سقوطه الأصلي إلى جميع أرجاء الكوب تقريبًا بشكل تلقائي دون تدخل أي عامل آخر. ما حدث هنا أن الحبر انتشر من منطقة ذات تركيز عالي إلى منطقة منخفضة التركيز. تلك هي نتيجة حتمية لقانون الديناميكا الحرارية الثاني الذي ينص على أن أي عملية في الكون تصحبها زيادة في العشوائية، أو في عدد الاحتمالات الممكنة التي يتواجد عليها نظام معين، وأن العمليات التي تتسبب مباشرة في زيادة عشوائية النظام تحدث بشكل عفوي. فعند انتشار المادة من حيز ضيق إلى حيز كبير نسبيًا، فإن عدد الأماكن والاحتمالات التتي يمكن أن يتواجد فيها كل جزئ بمفرده تزيد بالتبعية. وفي حالة انتشار الجسيمات، فإن سبب حدوث هذه العملية عفويًا هو أن الجسيمات في المنطقة الأعلى تركيزًا تمتلك قدرًا أكبر من الطاقة الحركية الحرارية مما يتيح لها اقتحام الأماكن الأقل تركيزًا حتى تتساوي تركيزات الجسيمات في كل منطقة.

تمت ملاحظة هذه الظاهرة في أشباه الموصلات. وتم الوصول إلى نتائج معملية مما يلي:

العلاقة بين تيار الانتشار وشدة تدرج تركيز الإلكترونات علاقة خطية طردية:

Idiff ∝ dn/dx

dn/dx هو معدل تغير التركيز بالنسبة للمسافة، أو ما يعرف بتدرج التركيز (concentration gradient).

وحتى تكون هذه المعادلة صحيحة من حيث الأبعاد، فيجب أن تكون على الصورة الآتية:

I = e*A*Dn*(dn/dx)

حيث Dn هو ثابت تناسب يسمى ثابت الانتشار، وA هو مساحة مقطع المادة شبه الموصلة.

وبجمع التيارين (تيار الإلكترونات والفجوات) نحصل على المعادلة الآتية:

J = e*(Dn*(dn/dx) – Dp*(dp/dx))

والإشارة السالبة التي تسبق الحد الخاص بتيار الفجوات تعني أن اتجاه التيار الكهربي المسبب عن الفجوات هو نفس اتجاه تناقص تركيز الفجوات، وأن اتجاه تيار الإلكترونات هو اتجاه تزايد تركيز الإلكترونات.

تعادل تياري الانتشار والإزاحة

ولكن في حالة عدم انتظام تركيز الشحنات في مادة شبه موصلة (كما هو الحال في الدايود والترانزستور)، كيف يمكن أن تنتقل الشحنة في حالة عدم وجود دائرة مغلقة تسمح بسريان الشحنات بصفة مستمرة؟

في الحقيقة فإن انتقال الإلكترونات من المنطقة الأعلى تركيزًا إلى المنطقة الأقل تركيزًا يتسبب في وجود مناطق موجبة الشحنة بسبب غياب الإلكترونات التي كانت تعادل شحنة النواة، بالإضافة إلى وجود مناطق سالبة الشحنة بسبب هجرة الإلكترونات إليها. وتلك الشحنات الفائضة تتسبب في وجود مجال كهربي يؤدي بدوره إلى ظهور تيار إزاحة في الاتجاه المضاد لتيار الانتشار. وتظل شدة تيار الانتشار في ازدياد حتى يتعادل معه تيار الإزاحة وتصل البللورة إلى حالة استقرار.[2]

 

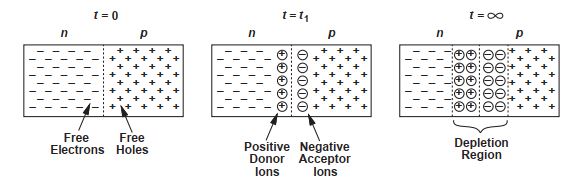
وباستخدام معادلات تيار الإزاحة والانتشار، والمعادلة التي تصف احتمال وجود الإلكترون في مستوى طاقة معين (Fermi-Dirac distribution function)، نحصل على العلاقة الآتية المشهورة باسم علاقة أينشتاين التي تربط بين ثابت الانتشار وثابت قابلية الحركة:

D/μ = (k*T)/q

حيث k هو ثابت بولتزمان، وT درجة الحرارة، وq شحنة الإلكترون. الكمية k*T)/q) تسمى فرق الجهد الحراري (Thermal voltage) ويرمز له بـ Vt، وهو يساوي في درجة حرارة الغرفة (27 مئوية) 26 mV.

شرح عمل الدايود وكيفية توظيفه في الدوائر الإلكترونية

فرق الجهد الداخلي للدايود

بسبب تركيبة الدايود الفريدة، ففيه يتولد جهد كهربي داخلي يمنع مرور المزيد من الشحنات داخل الدايود نتيجة لاختلاف تراكيز الشوائب في المنتصف. يمكن استنتاج معادلة فرق الجهد في ضوء ما عرفناه مسبقًا، وتحديدًا أنه في حالة الاستقرار فإن تيار الإزاحة يساوي في المقدار تيار الانتشار.

q*μp*E = q*Dp*dp/dx

وبذلك نحصل على المعادلة التفاضلية الآتية:

-μp*p*(dV/dx) = Dp*(dp/dx)

وبحل تلك المعادلة التفاضلية نحصل على:

Vi = Vt* ln(Pp/Pn)

حيث Pp هو تركيز الفجوات في المنطقة P (تركيز شحنات الأغلبية)، و Pn هو تركيز الفجوات في المنطقة N (تركيز شحنات الأقلية). وباستخدام المعادلات التي تصف تركيز أشباه الموصلات المطعمة، وتحديدًا قانون فعل الكتلة (mass action law) وقانون تعادل الشحنات في الفراغ (space charge neutrality)، نحصل على:

Vi = Vt*ln((Na*Nd)/ni^2)

حيث Na هو تركيز الشوائب المستقبلة في المنطقة P، وNd هو تركيز الشوائب المانحة في المنطقة N، وni هو تركيز الشحنات الحرة في بللورة شبه موصل نقية (بدون إضافة شوائب).

مما يعني أنه يجب أن تتغلب على فرق الجهد الداخلي حتى يسمح الدايود بسريان الشحنات من خلاله. ويجب كذلك أن توصل الدايود بمصدر جهد كهربي بانحياز أمامي. أما عند توصيل الدايود بانحياز عكسي فإن مصدر الجهد يقوم بتعزيز فرق الجهد الداخلي مما يمنع مرور الشحنات تمامًا (باستثناء تيار شحنات الأقلية وهو تيار ضئيل الشدة).[3]

عند توصيل الدايود بانحياز أمامي بمصدر جهد مقداره Vf نستنج من المعادلة السابقة أن تركيز شحنات الأقلية يزداد بشكل كبير جدًا:

Pn = Pp/(exp(Vi-Vf/Vt))

والشكل التالي يوضح تغير تركيز كل مجموعة من الشحنات على حدة:

 

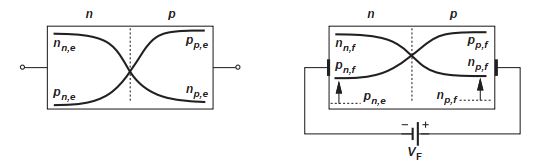
يمكن بذلك في النهاية استنتاج العلاقة بين الجهد والتيار في الدايود:

I = Is*(exp(V/Vt) – 1)

حيث Is يسمى تيار التشبع العكسي، وهو قيمة التيار الضئيلة في حالة التوصيل العكسي.

حيث أن:

Is = A*q*ni^2* (Dp/(Nd*Lp) + Dn/(Na*Ln))

A هو مساحة مقطع الدايود، L هو المسافة التي تنتشر فيها الشحنات (المنطقة ذات تركيز غير منتظم في منتصف الدايود). تلك المسافة تكون في العادة في حدود عشرات الميكرومترات. لاحظ أن الحدين بداخل الأقواس يصفان تيار كلًا من الإلكترونات والفجوات على الترتيب.[4]

هذه العلاقة تختلف تمامًا عما اعتدناه في الأجزاء الكهربية التقليدية مثل المقاومات والمكثفات، حيث أن قانون أوم البسيط ما هو إلا علاقة خطية بين الجهد والتيار مما يبسط المعادلات الرياضية بشكل مذهل. أما قانون الدايود بداخله الدالة الآسية والتي قد تعقد التعامل معه في أبسط الدوائر الكهربية. وسوف نتعامل كذلك مع علاقة مشابهة في الترانزستور. ولك أن تتخيل كم الحسابات الرياضية اللازمة إذا ما تعاملنا بهذا النموذج المعقد في الرقاقات الإلكترونية التي تحتوي على عدد مهول من تلك الترانزستورات.

نموذج الإشارات الكبيرة

من العلاقة السابقة بإمكاننا رسم منحنى العلاقة بين التيار والجهد في الدايود (Diode I/V characteristic):

نلاحظ أنه في حالة زيادة الجهد عن فرق الجهد الداخلي فإن شدة التيار تزداد بمعدل سريع جدًا حتى يكاد يكون فرق الجهد ثابتًا بينما تزداد شدة التيار. وهذا السلوك يشبه بحد كبير سلوك مصدر جهد كهربي. وفي حالة كان الجهد أقل من الجهد الداخلي فإن شدة التيار تكاد تكون معدومة، وذلك يشبه سلوك الدائرة المفتوحة التي لا تسمح بمرور أي تيار بغض النظر عن الجهد المفروض. وعمليًا فإن اعتبار الدايود مصدر جهد في التوصيل الأمامي ودائرة مفتوحة في التوصيل العكسي هو فرض مقبول تمامًا ولا يتسبب في تفاوت النتائج كثيرًا عن النتائج الدقيقة، وذلك في حالة ما إذا كنا نتعامل مع فروق جهد كبيرة نسبيًا فقط. أما إذا كنا نتعامل مع تغيرات طفيفة في الجهد فسوف نحتاج إلى نموذج آخر يصف الدايود بدقة أكبر. والنموذج الأول يعرف باسم نموذج إشارة كبيرة (large signal model).

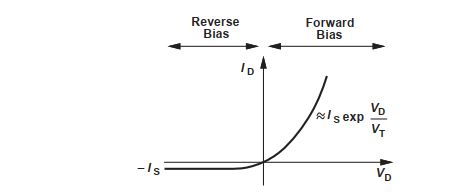
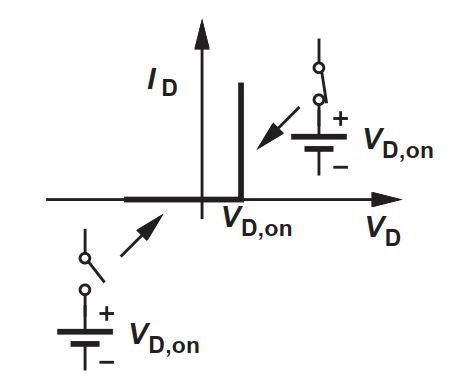
والتغيرات الكبيرة نسبيًا في فروق الجهد والتيار هي ما تعرف بالإشارة الكبيرة، ومن أمثلتها جهود المولدات الكهربية، وجهود المنازل، وجهود البطاريات. يستعمل هذا النموذج في حالة الدايود تحديدًا في عملية تقويم التيار المتردد (AC Current Rectification)، وعملية التقطيع (Clipping Circuits)…إلخ. وفي الترانزستور تحديدًا نستخدم هذا النموذج لوصف عمله كمفتاح أو أداة تخزين قيمة 0 أو 1، وكذلك من أجل حساب البارامترات الخاصة بعملية تكبير الإشارات الكهربية.[5]

نموذج الإشارات الصغيرة

في حالة التعامل مع تغيرات طفيفة في جهود الأجهزة الإلكترونية نتبع أسلوبًا آخر في وصف سلوكها. إذا ما قمنا بتحويل العلاقة الأسية بين الجهد والتيار إلى علاقة خطية، فسيتاح لنا أن نتعامل مع تلك الأجهزة على أنها أحمال كهربية خطية مثل المقاومات تمامًا، مما يجعل التعامل معها أسهل بكثير. فلو فرضنا أن الدايود عليه جهد كهربي معين وليكن Vq، فإذا قمنا بإضافة ذبذبات بسيطة على فرق الجهد نلاحظ زيادة وتناقص شدة التيار. وإذا كانت تلك الذبذبات صغيرة بشكل كافي، فمن المقبول على سبيل التقريب والتيسير أن نفترض أن العلاقة بين الجهد المتذبذب والتيار المتذبذب هي علاقة خطية، وذلك في حدود الذبذبات الصغيرة المحلية على الأقل.

 

 

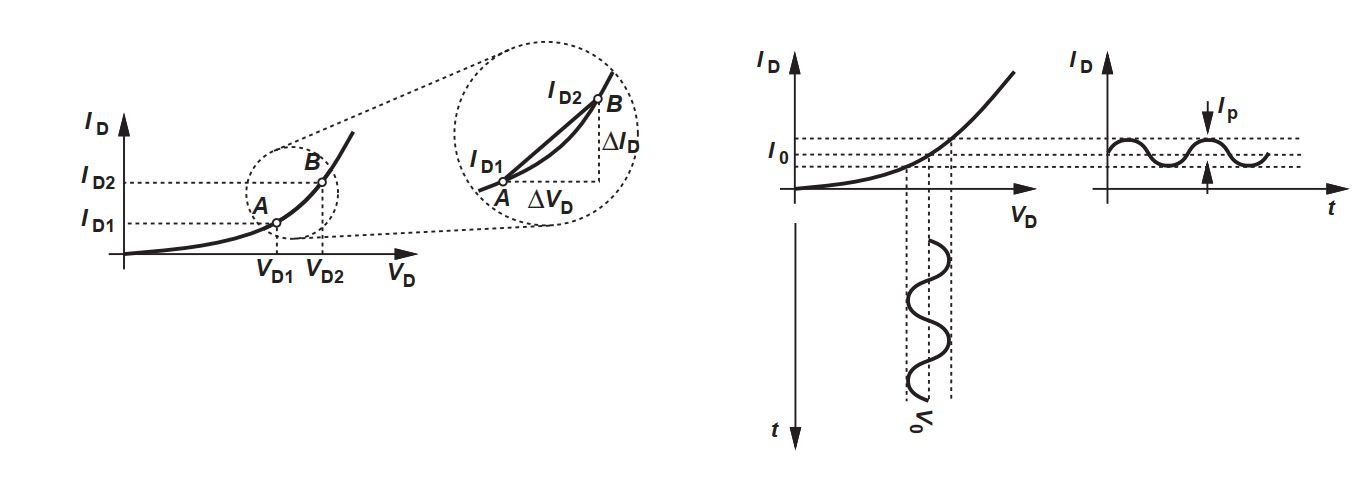
يمكن بذلك استنتاج قيمة المقاومة المكافئة لأداء الدايود أو أي جهاز إلكتروني عن طريق اشتقاق دالة التيار بالنسبة للجهد.

I ≈ Is*exp(V/Vt)

dI/dV @ (Vq, Iq) = (1/Vt)*Is*exp(Vq/Vt) = Iq/Vt

Rd = dV/dI = Vt/Iq

حيث أن Vq و Iq هي القيم التي يتذبذب حولها الجهد الكهربي والتيار على الترتيب، وRd هي المقاومة المكافئة للدايود (أي أن الدايود يتصرف مثل مقاومة ذات قيمة مساوية).

يستخدم هذا النموذج في حالة الدايود تحديدًا في عملية تنظيم الجهد الكهربي وحماية الأجهزة من التذبذبات الضارة عند تحويل التيار المتردد إلى تيار مستمر وغيرها من العمليات الأخرى. حيث أن الدايود يتميز بخاصية مقاومة الذبذبات وتقليل أثرها. ويقوم الدايود بمواجهة هذه الذبذبات عن طريق آليتين: تقليل أثر التغير في فرق الجهد الداخل (line regulation)، وتقليل أثر التغير في الأحمال المتصلة (load regulation).

وتكمن أهمية هذا النموذج الحقيقية في عملية تكبير الإشارات والذبذبات الكهربية التي يتم تحويلها بعد ذلك إلى ظواهر طبيعية محسوسة، مثلا الصوت، أو الضوء، أو الموجات الكهرومغناطيسية الأخرى. حيث أن تلك الإشارات ضعيفة جدًا في الطبيعة، وهي معرضة أيضًا للاضمحلال الذي يحكمه قانون التربيع العكسي، ومعرضة أيضًا إلى الاختلاط بمصادر تشويش متعددة. وتعد الترانزستورات والدوائر المتكاملة المكونة منها من أكثر الطرق شيوعًا في الوقت المعاصر لتحقيق هذا الغرض.[5]

وفي الحلقات المقبلة سوف نتعرف على تطبيقات أشباه الموصلات المتقدمة وعلى تركيبها مع شرح مبسط لكيفية عملها، وتحديدًا: الترانزستور، «السموس-CMOS»، المكبر العملياتي (op-amp). سوف نتعرف كذلك على كيفية عمل هذه الأجهزة كمكبرات إشارة كهربية أو كأجهزة تخزين. وبناءًا على النظريات والنماذج السابق شرحها، فسوف يتيسر علينا فهم الأساس العلمي الذي تعتمد عليه هذه الأجهزة.

 

إعداد: Hazem Mousa

مراجعة : Asmaa Masoud

المراجع:

[1] Fundamentals of Microelectronics, 2006, section 1.1

[2] Fundamentals of Microelectronics, 2006, section 2.1.3

[3] Fundamentals of Microelectronics, 2006, section 2.2.1

[4] Fundamentals of Microelectronics, 2006, section 2.2.3 & 2.2.4

[5] Fundamentals of Microelectronics, 2006, section 3.4