
كَتَبَ هذه المُفَارَقة ريَاضِيّ شَهير يُدعى (مارتن جاردنرـMartin Gardner) في عموده الخاص (ألعاب رياضيةـmathematical games) في مجلة (العلمي الأمريكي- scientific American) عام 1959 (1)،(2)
المفارقة:
- هنالك ثلاثة سجناء (A) و(B) و(C) في زنازين منفصلة ومحكوم عليهم بالإعدام.
- قرر الحاكم أن يختار عشوائيًا واحدًا منهم فقط ليُطلق سراحه، وأخبر حارس السجن بذلك الشخص.
- الحارس غير مصرح له بالإفصاح عن اسم الشخص الذي سيطلق سراحه.
- السجين (A) ترجى الحارس لأن يخبره عن واحد فقط سيتم إعدامه من السجينين الآخرين. إذا كان (B) سيتم العفو عنه قل لي(C). وإذا كان (C) سيتم العفو عنه قل لي(B) وإذا كنت أنا (A)من سيتم العفو عنه فارم عملة لتختار من ستخبرني باسمه (B) أو (C).
- قبل الحارس طلبه وأعطاه الاسم (B) أي أنه أخبره أن (B) سيُعدَم.
- فرح السجين (A) بهذه الأخبار حيث يعتقد الآن أن احتمالية إطلاق سراحه قفزت إلى ( 1/2 ) بدلا من (1/3 ) باعتبار أن فرصة النجاة مقسمة بالتساوي بين شخصين – بينه وبين (C) – بدلًا من أن يتشارك الثلاثة سجناء في فرصة واحدة.
- أخبر السجين (A) صديقه (C) بخبر إعدام زميلهما (B).
- فرح (C) بذلك على اعتبار أن (A) مازالت فرصته في النجاة (1/3 ) بينما ارتفعت فرصة (C) في النجاة إلى (2/3 ).
السؤال الآن أي منهما اعتقاده صحيح (A) أم (C)؟
سنستخدم طريقة (مخطط الشجرة- tree diagram) و(صيغة باي- Bayes’ formula) لحل هذه المفارقة :
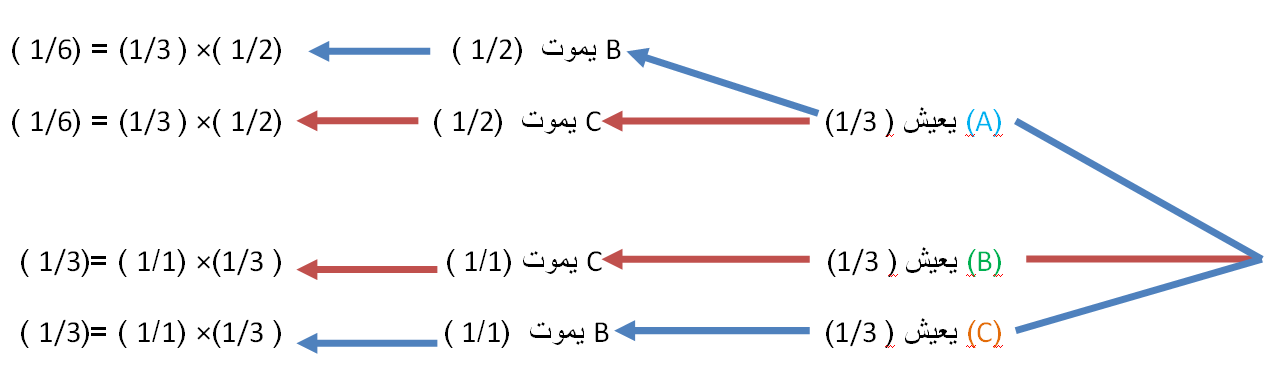
ولتبسيط المخطط: في البداية يمتلك السجناء الثلاثة فُرصًا متساوية للنجاة حيث أن مجموع نسب الفرص ( 1/3) +( 1/3) +( 1/3) = الواحد الصحيح أو (100/100).
-
إذا كان (A) سيعيش فإن الحارس سيرمي عملة ليخبره عشوائيًا إما أن (B) أو (C) سيموت بفرص متساوية لكل منهما وهي (1/2).
-
إذا كان (B) سيعيش فإن الحارس سيقول أن (C) سيموت بنسبة 100/100.
-
إذا كان (C) سيعيش فإن الحارس سيقول أن (B) سيموت بنسبة 100/100.
وبما أن الحارس أخبر أن (B) سيموت، إذًا سنستبعد احتمال أن (B) سيعيش منذ بداية التجربة وفي الحالة الأولى أن (A) سيعيش سنستبعد موت (C) من الاحتمال حيث أن موت(B) مؤكدٌ الآن. والاحتمالات المُستبعدة مُمَثلة في الخطوط الحمراء.
إذًا المسارات الزرقاء تحدد احتمالات هذه التجربة وهي:
أن احتمالية نجاة (A)= (1/6).
أن احتمالية نجاة (C)= ( 1/3) =(2/6 ). أي أن (C) لديه فرصة للنجاة أكبر من
(A) بمقدار الضعف.
إذًا، بما أن احتمالية نجاة (A) منذ البداية (1/3) وبما أن فرصة (C) هي الضعف فتكون في النهاية (2/3).
(صيغة باي-Bayes’ formula):
فلنفرض أن A وB وC هي الأحداث التي تُمَثِّل إطلاق سراح السجناء الثلاثة (A) و(B) و(C) على الترتيب.
ولنفرض أن الحدث b يُمَثِّل ما قاله الحارس أن السجين (B) لن يطلق سراحه.
وباستخدام صيغة باي فإن احتمالية أن يُطلق سراح (A) هي:
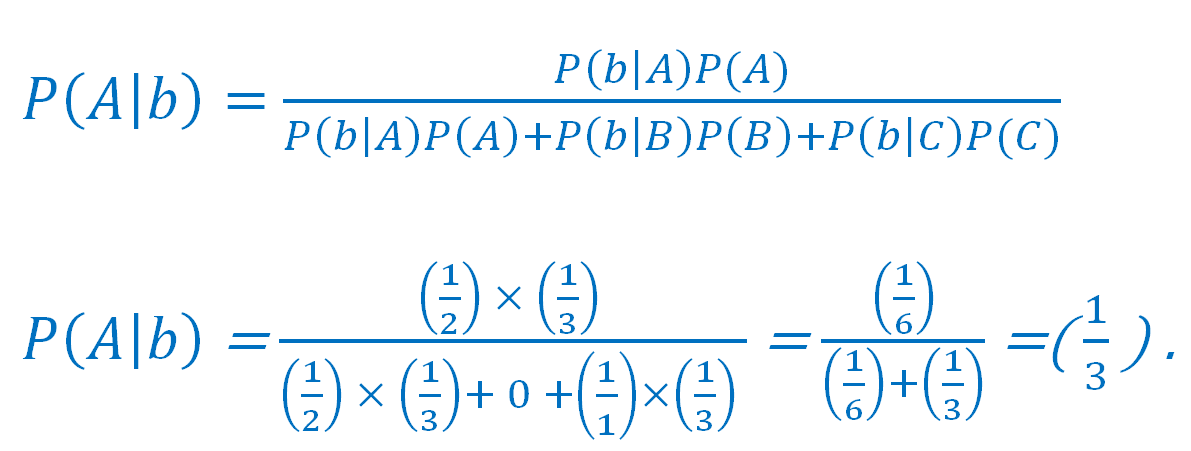
إذا احتمالية إطلاق سراح (C) هي:
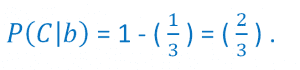
إعداد : Ahmed Hosiny
مراجعة: Mohamed Sayed Elgohary
تصميم:Bothaina Mahmoud
#الباحثون_المصريون
المصادر:
Gardner, Martin (October 1959). “Mathematical Games: Problems involving questions of probability and ambiguity”. Scientific American 201 (4): 174–182. doi:10.1038/scientificamerican1059-174
Gardner, Martin (1959). “Mathematical Games: How three modern mathematicians disproved a celebrated conjecture of Leonhard Euler”. Scientific American 201 (5): 188. doi:10.1038/scientificamerican1159-18

