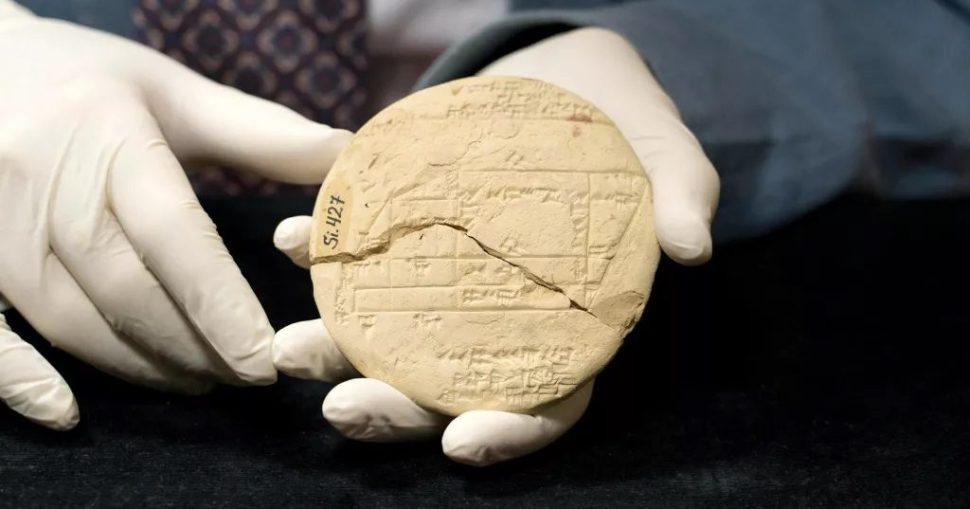
كشف لوح طيني عمره 3700 عام أنَّ البابليِّين القدماء قد فهموا نظريَّة فيثاغورس قبل ولادة الفيلسوف اليوناني بأكثر من 1000 عام!

كان مسَّاحو الأراضي في بابل القديمة يستخدمون اللوح المعروف بـ(Si.427) لرسم حدود دقيقة. العلامات المسماريَّة المحفورة عليه -والتي تُشَكِّل جدولًا رياضيًّا- كانت تمكِّن قارئه من عمل مثلَّثات صحيحة دقيقة؛ ممَّا جعل هذا اللوح أقدم مثال معروف للهندسة التَّطبيقيَّة.

يُعرَض اللوح -الذي يرجع تاريخه إلى ما بين 1900 و1600 ق.م- حاليًّا في متحف اسطنبول الأثريّ، بعد أن اكتشفته بعثة أثريَّة فرنسيَّة عام 1894م في ما يعرف الآن بالعراق، ولكن لم يتمّ اكتشاف دلالة العلامات المحفورة عليه إلى الآن.

نظريَّة فيثاغورس بدائية

صرَّح دانيال مانسفيلد عالم الرياضيات في جامعة نيو ساوث ويلز بأستراليا، ومكتشِف معنى اللوح، قائلًا:

إنَّ من المُسلَّم به عمومًا أنَّ علم حساب المثلَّثات طُوِّر بواسطة الإغريق القدماء؛ بدراستهم للسَّماء ليلًا في القرن الثاني قبل الميلاد، ولكن اتَّضح أنَّ البابليِّين قد طوَّروا نموذجهم الخاص البدائي من علم حساب المثلثات؛ لحلّ المشكلات المتعلِّقة بقياس الأرض، لا السَّماء.

وفقًا لمانسفيلد فإنّ اللوح (Si.427) هو المثال الوحيد لوثيقة مساحيَّة، أو لمخطَّط استخدمه مسَّاحو الأراضي لتحديد حدود الأرض في الفترة البابليَّة القديمة؛ فهو هنا يخبرنا بالتَّفاصيل القانونيَّة والهندسيَّة عن حقل تمَّ تقسيمه بعد بيع جزءٍ منه.

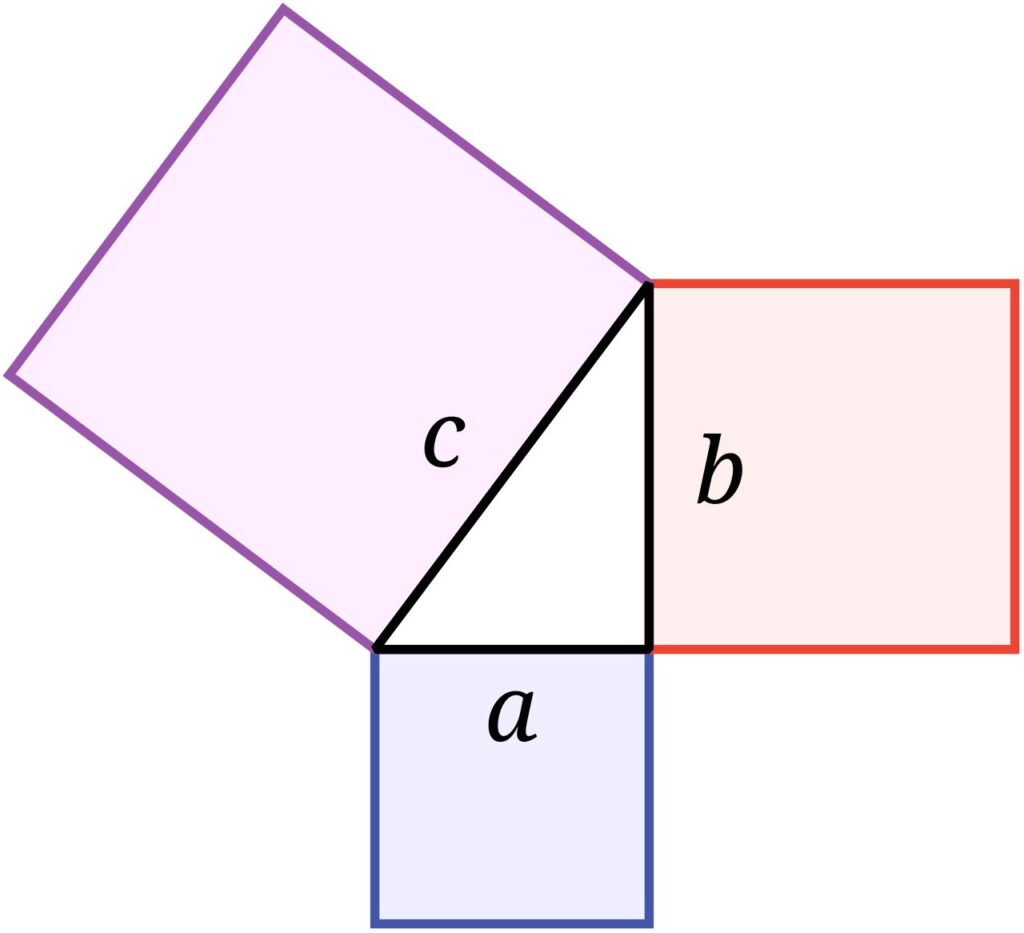
يعرض اللوح تفاصيل حقلٍ مستنقعيٍّ به أبنية مختلفة، كان أحدها عبارة عن برج، وتمَّ نقشه بثلاث مجموعات من ثلاثيَّات تحقِّق نظريَّة فيثاغورس: (ثلاثة أعداد صحيحة مجموع مربَّعي الأوَّلين يساوي مربَّع الثَّالث)، وكانت الثلاثيَّات كما يلي: (3،4،5)، (8،17،18)، (5،12،13). كانت تُستخدَم على الأرجح للمساعدة في تحديد حدود الأرض.

وعلى الرَّغم من أنَّ اللوح لا يعبِّر عن النَّظريَّة بصيغتها الجبريَّة المألوفة؛ إلَّا أنَّ التَّوصُّل إلى هذة الثلاثيَّات يتطلَّب فهم المبدأ العام الذي يحكم العلاقة بين طول الأضلاع والوتر.

لوح آخر

في عام ٢٠١٧، اكتشف مانسفيلد لوحًا آخر من نفس الفترة اسمه (Plimpton 322)، يحتوي على جدول مثلَّثيّ آخر. وبمجرَّد أن رأى اللوح (Si.427)، استطاع جمع الخيوط ببعضها، والتوصُّل إلى أنَّ البابليِّين القدماء كانوا يستخدمون نظريَّتهم المثلثيَّة البدائيَّة لتقسيم قطع الأرض. ويعتقد مانسفيلد أنَّ اللوح (Si.427) يعود إلى ما قبل تاريخ اللوح (Plimpton 322)، بل وربَّما يكون مصدر إلهام له.

صرَّح مانسفيلد -مُشيرًا إلى حقيقة أنَّ المثلَّثات القائمة المختلفة تحتوى على زوايا داخلية مختلفة- قائلًا:

توجد العديد من المثلَّثات القائمة ذات الأشكال المختلفة، ولكن يمكن استخدام عدد قليل منها بواسطة مسَّاحي الأراضي البابليِّين، ويُعَدُّ اللوح (Plimpton 322) دراسة منهجيَّة لتلك الأشكال لمعرفة المفيدة منها.

وأضاف أيضًا:

في تلك الفترة، بدأ النَّاس يفكرون في الأراضي كملكيَّة خاصَّة؛ مما حذا بهم لتعيين حدود مناسبة لإقامة علاقات جيرة جيِّدة مع الآخرين. فما يخبرنا اللوح به هو أنَّه تمَّ تقسيم الحقل وتعيين حدود جديدة له.

ومع أنَّ الأسباب الكامنة وراء حسابات حدود الأرض على اللوح ليست واضحة تمامًا؛ إلَّا أنَّ اللوح يذكر نزاعًا حول أشجار نخيل على الحدود بين ممتلكات شخص بارز يُدعى (Sin-bel-apli) ومالكة أرض ثريَّة، ويعلِّق مانسفيلد على ذلك قائلًا: «من السَّهل معرفة مدى أهمِّيَّة دقَّة تعيين حدود الأراضي في حل النِّزاعات بين الشَّخصيَّات ذات النُّفوذ.»

وبالرَّغم من مرور 1000 عام بين صناعة تلك الألواح وبين ميلاد فيثاغورس عام 570 ق.م، والذي صاغ النَّظريَّة في شكلها الذي يدرسه التَّلاميذ في وقتنا الحالي؛ فإنَّ الخبراء يعلمون منذ زمن بعيد أنَّ الإغريق قد تلقَّوا الدِّراسات الرِّياضيَّة من المصريِّين، الذين تلقَّوها بدورهم من البابليِّين. إلَّا أنَّ ما يثير دهشة مانسفيلد هو مستوى التَّطوُّر النَّظريّ الذي تكشفه هذه الألواح عن البابليِّين القدماء، الذين عاشوا في هذه المرحلة المبكِّرة من تاريخ البشريَّة، وأضاف:

لم يتوقَّع أحد أنَّ البابليِّين كانوا يستخدمون ثلاثيَّات فيثاغورس بهذه الطريقة، التي هي أقرب للرِّياضيات البحتة المستوحاة من المشاكل العمليَّة التي واجهتهم في ذلك الوقت.