من مكتبة الإسكندريَّة

تبدأ قصة اليوم من أرض الكنانة، أرض مصر، وتحديدًا في أعظم مكان قاد الدنيا في العلوم في وقتٍ ما مضى، الإسكندريَّة التي درس فيها إقليدس. والتي وُلد وعاش ومات فيها بطليموس، حيث ألّف بها كتاب «المجسطي»، الذي يُعَدّ أول كتاب في التاريخ في علم الفلك.

الإسكندريَّة التي وُلدت وعاشت وماتت بها أول عالمة رياضيّات في تاريخ البشرية نمتلك عنها معلومات مؤكدة ومفصلة إلى حد ما وهي هيباتيا؛ هيباتيا التي ماتت بشكل بشع، فقد حاربها المسيحيون ونزعوا ملابسها وجروها في شوارع المدينة ثم سلخوا جلدها حتى ماتت، ثم أحرقوا جسدها بالنيران. ومع إحراق جسد هيباتيا بالنار فقد أُحرِقت معه كل العلوم والأفكار، فقد انتشر الجهل بعدها لمدة تزيد على الـ 1300 عام، ولم تظهر خلال هذه القرون عالمة رياضيات واحدة، حتى جاءت ماريا أنيزي في القرن الثامن عشر في إيطاليا.

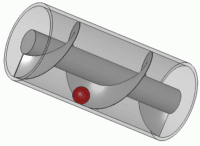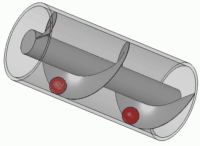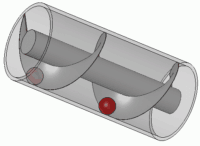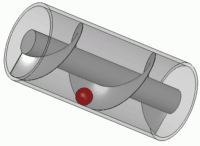
الإسكندريُّة التي طوّر فيها أرخميدس مضخة المياه ذات الشكل اللولبيّ، والتي ما زالت تُستخدم في الري حتى يوم الناس هذا. [1]

الإسكندريَّة التي مات فيها أرسطوطاليس، والتي تمت فيها أول محاولة علميّة في التاريخ لقياس محيط كوكب الأرض، حيث كانت قياساته غاية في الدِقُة وبنسبة خطأ لا تتعدى الـ 2٪. [2]

فكرة تخالف إجماع العلماء

تبدأ القصة من مكتبة الإسكندريُّة، التي كانت أول جامعة عرفها التاريخ، حين بدأ عالم الرياضيات اليوناني أرسطرخس (بالإنجليزيَّة: Aristarchus) بالتفكير في سؤالٍ لم يكن مطروحًا في ذلك الوقت، سأل نفسَه سؤالًا: تُرى، ماذا لو لم تكن الأرضُ هي مركز الكون، وإنما مجرد جسم يدور حول الشمس؟

يبدو السؤال سخيفًا بالنسبة لأشخاصٍ يعيشون في القرن الحادي والعشرين، ولكن بالنسبة لشخصٍ كان يعيش في زمنٍ بعيد -ثلاثة قرون قبل ميلاد السيد المسيح- كان هذا السؤال ثوريًّا وجديدًا ومختلفًا إلى أقصى حد. ولكن للأسف لا نملك أدلّةً تخبرنا لماذا فكّر أرسطرخس في هذه الفرضيّة، وما هي الأدلّة التي توصل إليها ليقول بذلك القول الذي خالف فيه إجماع العلماء في وقته.

لسوء الحظ اُتُهِمَ بالزندقة بسبب نظريته تلك، ولكن لحسن الحظ نجى كتابٌ واحد ووصل إلينا وهو كتابه «أحجام الشمس والقمر وأبعادهما». وتعتبر القيمة العلمية الرئيسة لهذا الكتب هو أنه يُعتبر أول محاولة علميّة حقيقة لحساب المسافة بين الأرض والقمر والشمس وحجم كل واحد منهم بالنسبة للآخر.

وبالرغم من أن أرسطرخس لم يتوصل إلى نتائج صحيحة، فقد ظنَّ أن الشمسَ تبعد عنَّا بما يساوي 19 مرة ضعف بُعد الأرض عن القمر، ولكن في الحقيقة أن الشمس تبعُد بـ 400 مرة (تقريبًا) ضعف بُعد القمر من الأرض، إلا أنه يكفيه أنه بذل جهده وحاول وجرّب وتعلّم وكان له السبق التاريخي في أول محاولة علميَّة لحساب تلك القيم. [3]

وتقديرًا لمحاولة هذا الرجل العظيم لقياس المسافة بين الأرض والقمر والشمس، فقد أطلقت وكالة الفضاء الأمريكيَّة ناسا اسمه على هضبة وفوهة على سطح القمر، تخليدًا لذكرى الرجل الذي ارتبط اسمه بالقمر والشمس. [4]

من هذا الرابط تستطيعون مشاهدة فوهة أرسطرخس على سطح القمر، بل ومشاهدة القمر كله بجودة عالية وبتقنية الـ 3D إن أردتم.

ولكن، أليس من حقنا أن نسألَ الآن، وكيف توصلنا إلى معرفة المسافة الحقيقة بين الأرض والقمر، وبين الأرض والشمس؟ ما الذي حدث كي يمكننا من الوصول إلى هذه الدرجة العالية من الدِقّة حتى صرنا نقيسها الآن بالكيلو مترات، وهي تقريبًا 384,400 كم.

قبل أن نجيب عن هذا السؤال، أردت أن أوضح لماذا قلتُ في السطر السابق إن المسافة بين الأرض والقمر هي (تقريبًا) 384,400 كم؟ لماذا بعد كل ما توصلنا إليه من علم وتكنولوجيا ومعرفة بالقمر بشكل جيد، وبعد أن نزل الإنسان مرات عديدة على سطح القمر والتي تتطلب معرفة دقيقة جدًا، لماذا بعد هذا كله نذكر المسافة بشكل مُقرَّب وليس بشكل محدد؟

أقول بدايةً إن القضية ليست في قلة معرفتنا أو عجز أجهزتنا، ولكن القمر يدور بشكل بيضاوي حول الأرض، وهذا يعني أن المسافة تتغيّر دائمًا وبشكل مستمر بينه وبين الأرض، ففي أقرب نقطة من الأرض يكون القمر على مسافة 360,000 كم، وفي أبعد نقطة من الأرض يكون القمر على مسافة تصل إلى 405,000 كم.

والسؤال الآن: بغض النظر عن حركة القمر وقُربه وبُعده من الأرض، ما هي الدِقّة التي نستطيع بها حساب المسافة بين الأرض والقمر في نقطة معينة؟ أقول: يمكن حساب المسافة بين الأرض والقمر بدِقّة عالية، ليست بالكيلومترات ولا بالأمتار ولا حتى بالسنتمترات، بل بدِقّة تصل إلى 1.1 ميليمتر. وما بين حساب أرسطرخس للمسافة في الإسكندرية وبين حسابنا اليوم بدِقّة تصل إلى 1 ميليمتر، قصة كُتبت حروفها بدماء العلماء، وفصولها بعرق الجبهات، ما بين أرسطرخس في الإسكندرية وناسا في الولايات المتحدة، قصة عظيمة سأرويها لكم اليوم. [5]

طريقة حساب أرسطرخس

في هذا الفيديو القصير، أوضح لكم كيف تمكن أرسطرخس من حساب النسبة بين بُعد الشمس والقمر عن الأرض، ما الطريقة التي استخدمها؟ ولماذا كانت حساباته خاطئة؟

كانت تلك محاولة بدائيّة ورائعة من أرسطرخس، حتى جاء بعده العالم الجليل هيبارخوس (بالإنجليزيَّة: Hipparchus) وطوّر ما فعله زميلُه السابق، ووصل بدِقّة إلى المسافة بين الأرض والقمر، بل حتى وصف أطوار القمر وحركته وحركة الشمس وصفًا دقيقًا وفريدًا. [6]

أول محاولة بالأدوات الحديثة

ومن حينها ولمدّة مئات السنين ظلَّ العلماء يطوّرون أجهزتَهم وقياساتهم وأدواتهم لرصد القمر وتحديد حركته على وجهٍ أكثر دِقّة، حتى بداية ستينيات القرن الماضي، وبعد اختراع الليزر بعامين فقط، استخدمه البروفيسور لويس سمولين (بالإنجليزيَّة: Louis Smullin) في جامعة (MIT) بالولايات المتحدة في إرسال إشعاعات منه إلى القمر ثم انتظارها لتعود فوتونات الضوء منعكسة على الأرض، وبما إننا نعلم على وجه التحديد سرعة الموجات الكهرومغناطيسيّة، فما علينا إلا حساب الوقت اللازم للإشعاع ذهابًا وإيابًا إلى القمر، ثم ضرب السرعة في الزمن، فنحصل بذلك على المسافة على وجه الدقة. [7]

ويمكن تحقيق ذلك من خلال المعادلة الآتية: المسافة = (سرعة الضوء x الزمن) ÷ 2

نحن نريد معرفة المسافة، ونعلم أن سرعة الضوء ثابتة، فما علينا إلا حساب الزمن الذي تستغرقه فوتونات الضوء حتى تصل إلى القمر وتعود إلى الأرض، ثم نقسم بعد ذلك على 2.

كانت تلك ثورة عملاقة في استخدام أدوات حديثة بدلًا عن الأدوات القديمة في القياس، وبعدها بعام واحد فقط، قام العلماء الروس في الاتحاد السوفيتي بتجربة شبيهة لها تمامًا من نفس النوع باستخدام الليزر أيضًا لحساب المسافة بيننا وبين القمر. [8]

المشكلة الأساسيّة في هذه الطريقة من القياس، أنهم يستخدمون سطح القمر كعاكس للضوء، ولكن مثل هذه الأسطح ليست عاكسةً بشكلٍ جيد للضوء، فكان لا بد من إيجاد شيء يوضع على سطح القمر ليعكس الضوء الساقط عليه بشكل كامل.

مرآة على سطح القمر

تمت هذه القفزة العلميّة بإضافة عاكس جيد بدلًا من استخدام سطح القمر نفسه في رحلة أبوللو 11، حيث حمل رائد الفضاء نيل أرمسترونج وباز ألدرين معهما عاكسًا ليضعوه على سطح القمر.

كانت تلك نقلة نوعيّة من الدقة في حساب المسافة بين الأرض والقمر بشكل دقيق، حتى وصلت نسبة الخطأ في المسافة إلى الأقل في التاريخ، وبمعدل 7 أمتار فقط كحد أقصى في نسبة الخطأ.

ونتيجة هذه الدقة المتناهية، فقد أرسلت وكالة الفضاء الأمريكيّة ناسا عواكس أخرى في رحلاتها التالية، فأرسلوا عاكسًا في رحلة أبوللو 14، ثم عاكسًا ثالثًا في رحلة أبوللو 15. ثم بعد ذلك أرسل الاتحاد السوفيتي عاكسًا إلى سطح القمر في رحلة (Lunokhod 1) عام 1970، ثم تبعه بعاكس آخر في رحلة (Lunokhod 2) عام 1973.

الأمر الجيّد في هذه العواكس إنها لا تحتاج كهرباء ولا مصدر للطاقة لتعمل، لذا فهي منذ أن وضعت على سطح القمر منذ خمسين عامًا وهي إلى الآن مستمرة في العمل بشكل متواصل.

ولكن أيضًا رغم هذه التطوّرات الجبارة، إلا أن الحساب لم يكن دقيقًا، فلم تكن المشكلة في العاكس بشكل أساسي، ولكن المشكلة كانت في حساب الوقت بدقة عالية، فكانت نسبة الخطأ في البداية تصل إلى 150 نانو ثانية، حتى وصلت إلى نسبة خطأ لا تتعدى الـ 2 نانو ثانية، في نهاية السبعينيات. [8]

ولا عجب أبدًا فقد وصل د. أحمد زويل (الذي درس في جامعة الإسكندريُّة) إلى قياس حركة الجزيئات في مستوى زمني يصل إلى الفيمتو ثانية في نهاية التسعينيات. [9]

حساب المسافة بالملليمتر

ظلَّ العلماء يطورون أجهزة القياس والزمن حتى توصلوا في بدايات عام 2009 إلى دقة في حساب المسافة بيننا وبين القمر بنسبة خطأ لا تتعدى الـ 1 ملليمتر. [5]

ثم تمت محاولات بعد ذلك في عام 2012 وفي تعاون مشترك بين الولايات المتحدة وإيطاليا لإرسال عاكس إلى سطح القمر يتناسب مع دقة علوم القرن الحادي والعشرين، فقد قال العلماء الإيطاليون أنهم توصلوا إلى دقة تصل إلى 0.1 من الملليمتر الواحد. بل قالوا إن دقة الجهاز الجديد ستصل إلى 100 مرة أفضل من الدِقّة الحاليّة. كان من المفترض أن يطلق العاكس في شهر يوليو من عام 2020 إلى القمر ضمن برنامج (MoonLIGHT)، ولكن لسوء الحظ في شهر فبراير الماضي تم إلغاء الإطلاق. [10،11]

أينشتاين يفوز مرة أخرى

نتيجة لهذه الدِقّة العالية من القياس، أراد العلماء التأكد من نظرية النسبية العامة للعالم الألماني ألبرت أينشتاين، ففي عام 1968، قام الفيزيائي الأمريكي كينيث نوردفيدت (بالإنجليزيَّة: Kenneth Nordtvedt) بوضع نظرية النسبيّة العامة لأينشتاين تحت المجهر، لفحصها مرة أخرى بعد تمكننا من معرفة القياسات بشكل أوضح، وجاءت نتائجه متوافقة تمامًا مع ما تنبأه أينشتاين قبل ذلك بعقود. [12]

بعد ذلك بنحو 40 عامًا، وفي عام 2012، أراد العلماء التركيز على جانب واحد من إحدى جوانب النسبية العامة، وهو مبدأ التكافؤ (بالإنجليزيَّة: Equivalence Principle)، وباستخدام أجهزة القياس الحديثة لحساب المسافة بين الأرض والقمر ومعرفة مدار القمر بشكل غاية في الدِقّة، توصلوا إلى أن الحسابات الحالية تتوافق بشكل مذهل مع ما تتنبؤه النظرية، بنسبة خطأ صغيرة جدًا تساوي (−0.8 ± 1.3) × 10⁻¹³، أي بنسبة خطأ تساوي واحد من 10 تريليون. [13]

تحقيق حلم بدأ من الإسكندريَّة

كانت تلك قصة قصيرة من قصص العلم الممتعة، بدأت من مكتبة الإسكندريَّة في مصر، ثم أكمل فصولَها علماءُ العالم من مختلف البلدان والقارات، حتى انتهت إلى الفضاء الخارجي، يوم أن سار أول إنسان على سطح القمر ووضعوا العاكس القمريّ ذا الدِقُة العالية. بدأت بفكرة وُصفت بأنها مخالفة لإجماع العلماء في وقت أرسطرخس، حتى تحولت إلى حقيقة في وقتنا الحاضر، بل إلى أبعد مما أراده أرسطرخس وحلم به.