تخيل أنه في احد الايام ذهب أخوين توأم، واشتروا ساعات مُتطابقة، وتم ضبطها على نفس التوقيت تمامًا. وبعدها ذهب أحد الأخوين إلى الفضاء بصاروخ فضائي يسير بسرعة تصل إلى حوالي 90% من سرعة الضوء، بينما يقف الاخ الآخر على الأرض ويُشاهد أخاه في الفضاء بمنظار قوي جدًا.
تخيل أن الأخ الذي في الصاروخ كان يضع مصباحاً على أرضية الصاروخ، ومرآة في سقفه، كما هو واضح في الصورة في القطعة a.
بينما الاخ الاخر الذي يقف على الارض يُشاهد ما يحدث في الصاروخ عند اخيه، كما في الصورة b.

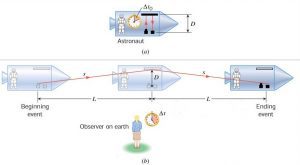
هل الوقت الذي سيقيسه الاخ الذي على الصاروخ للضوء حين يخرُج من المصباح ويصطدم بالمرآة ثم يعود لأرضية الصاروخ سيكون مُساوي للوقت الذي سيقيسه الاخ الاخر الذي على الارض لنفس شُعاع الضوء الذي يخرُج من المصباح في أرضية الصاروخ ليصطدم بالمرآة ويعود للأرض؟ أم انه سيقيس وقت مُختلف؟
دعونا نُسمي الأخ الذي على الصاروخ «ص»، والذي على الأرض «أ»، والوقت الذي سيقيسه ص بـ ΔTo، والوقت الذي سيقيسه أ بـ ΔT.
إذًاً فما نُحاول فعله الآن هو إيجاد علاقة تربط ΔTo بـ ΔT.
يُمكننا استخدام نظرية فيثاغورس، فكما ترى بالصورة، فالمسافة التي انتقلها الضوء من المصباح للمرآة بالنسبة لرؤية ص هي D.
والمسافة التي انتقلها الضوء من المصباح للمرآة بالنسبة لرؤية أ هي s.
والمسافة L هي المسافة التي تحركها الصاروخ في الوقت الذي انتقل فيه الضوء من المصباح للمرآة.
بتطبيق نظرية فيثاغورس، نجد ان:
s^2=D^2+L^2
طبعًا المسافة = الوقت مضروب في السرعة (v=d/t –< d=vt)
ولكن لو قُلنا ان الوقت هو ΔT الذي قاسه أ، فهذا الوقت الكُلي، أي انه وقت 2L وليس L فقط.
فإذًا: 2L/v = ΔT
أي ان: L= ΔT*v/2
وهُنا v هي سُرعة الصاروخ، وليست سُرعة الضوء، لإن 2L هي المسافة التي قطعها الصاروخ وليس الضوء.
من هُنا، نستنتج أن: s^2 = D^2 + (ΔT*v/2)^2
أي ان: s = (D^2 + (ΔT*v/2)^2 )^1/2
ولكن الضوء لم يقطع مسافة s فقط، بل قطع مسافة 2s، الموضوع سهل، سنضرب المُعادلة كلها في 2:
2s = 2* ( D^2 + (ΔT*v/2)^2 )^1/2
وهُنا 2s هي المسافة التي قطعها الضوء، وليس الصاروخ، وبالتالي فإن:
2s = ΔT * c
حيث ان c هي سرعة الضوء، والضوء سرعته ثابتة في الفضاء.
وطبعًا ΔT لم تتغير سواء كُنا نتكلم على الصاروخ او الضوء، لإن ΔT هو الوقت الذي استغرقه الصاروخ ليقطع مسافة 2L عندما كان يقطع الضوء مسافة 2s.
من هُنا، فإن:
ΔT*c = 2* ( D^2 + (ΔT*v/2)^2)^1/2
بتربيع طرفي المُعادلة، ينتُج الآتي:
ΔT^2 * c^2 = 4 *(D^2+ ΔT^2 * v^2/4)
ΔT^2 * c^2 = 4D^2 + (ΔT^2 * v^2)
ΔT^2 = 4D^2/c^2 + (ΔT^2 * v^2)/c^2
ΔT^2 = (2D/c)^2 + (ΔT^2 * v^2)/c^2
وهُنا يجب أن نُلاحظ أن (2D/c) هي الوقت الذي قاسه ص وهو على الصاروخ، لإن 2D هي المسافة التي قطعها الضوء بالنسبة لرؤية ص، وc هي سُرعة الضوء، وبالتالي فإن: ΔTo = 2D/c
إذًا: ΔT^2 = ΔTo^2 + (ΔT^2 * v^2)/c^2
بالتالي: ΔTo^2 = ΔT^2 – (ΔTo^2 * v^2)/c^2
ΔTo^2 = ΔT^2 * (1 – v^2/c^2)
وبالتالي:
ΔTo = ΔT * (1 – v^2/c^2)^1/2
اخيرًا:
ΔT = ΔTo / ( 1 – v^2/c^2 )^1/2

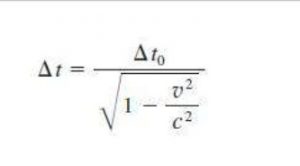
هذه هي مُعادلة تمدد الزمن- Time Dilation.
يتضح من هذه المُعادلة أن الوقت الذي سيقيسه ص سيختلف عن الوقت الذي سيقيسه أ باختلاف السُرعة.
بتطبيق المُعادلة على موقف الأخوين التوأم، سنجد أنه إذا كان الأخ ص يسير بسرعة 90% من سرعة الضوء، فستساوي الثانية عند ص حوالي 3.16 ثانية عند أ، وبالتالي لو افترضنا أن ص ظل في الفضاء لمُدة 3 سنوات في الصاروخ الذي يسير بسرعة الضوء، يكون قد مر على أخيه التوأم ما يُقارب الـ 9 سنوات ونصف، أي انه حين يعود للأرض سيجد أن أخاه التوأم أصبح أكبر منه بحوالي 6 سنوات ونصف!
تلك هي مُعادلة تمدد الزمن التي طرحها آينشتاين في نظريته النسبية، وهي تُطبق طُوال الوقت، لكننا لا نشعر بها ولا يستطيع احد مُلاحظتها إلا في المعامل والتجارب الفيزيائية المُتقنة بسبب صِغَر حجم السرعات التي نراها في حياتنا اليومية بالمُقارنة بسرعة الضوء.

المصدر:
Physics – John Cutnell
إعداد: Michael M. Louis