يُعرف الضغط بإنه القوة العمودية التي يؤثر بها مائع لكل وحدة مساحة، أو هو -بشكل أبسط- ناتج قسمة القوة العمودية على مساحة السطح التي تؤثر عليها تلك القوة. وقد يسأل القارئ: «ولمَ المائع فقط، أوما رأيت أن الجسم الصلب إذا وضعناه على سطح فإنه يضغط على هذا السطح؟». لا يا عزيزي القارئ، فهذا الذي ذكرته يسمى بالإجهاد الميكانيكي العمودي (Normal Stress) وهو ليس محلًا لدراستنا في ميكانيكا الموائع، لكنه هو نفسه الضغط إن أردت ألا تلتزم بتلك التسمية. وعندما نتعامل مع الضغط يظهر لنا نوعان من الضغط: الضغط الفعلي المقاس عند أي نقطة في المائع وهذا يسمى بالضغط المطلق (Absolute Pressure).
قد تكون لاحظت عندما يملئ عامل صيانة السيارات الإطار بعد أن فَرَغ من الهواء، أن عداد الضغط الذي لديه يبدأ قراءته من الصفر، هل معنى هذا أن الضغط الفعلي للهواء داخل الإطار مساوٍ للصفر؟ وما معنى أن يكون الضغط الفعلي للهواء مساوٍ للصفر؟
معنى أن الضغط الفعلي مساوٍ للصفر أي أنه لا يوجد أي جزيئ هواء داخل الإطار أو أن جزيئات الهواء داخل الإطار في حالة سكون تام، وكلتا الحالتين مستحيلتان. الأمر كله أن هذا الضغط الذي يقيسه العداد هو الفرق بين الضغط الجوي والضغط الفعلي للإطار. وهذا الضغط يسمى بالضغط اللا جوي (gauge pressure).
وحدات قياس الضغط
للضغط وحدات كثيرة، تختلف القيمة الفعلية لكل وحدةِ منها، ولكنها كلها تتفق في شيء، أنها ناتج قسمة قوة وزن معين على وحدة معينة من المساحة. فهَبْ أنك أردت أن تعرف وحدة قياس جديدة للضغط، وتسميها باسمك، فالأمر حينئذٍ يسير. كل ما عليك هو أن تأخذ شيئًا ثابت الوزن، وآخر ثابت الطول وتعرف وحدة قياس الضغط بها.
وعلى هذا المنوال، تجد الباسكال (Pascal ويرمز لها بالرمز Pa) وهي وحدة الضغط الأساسية، والتي تساوي الضغط الناتج من تأثير قوة عمودية مقدارها نيوتن واحد على سطح مساحته مترٌ مربعٌ واحد. ووحدة الضغط الجوي (atmospheric pressure ويرمز لها بالرمز atm) وهي تساوي مقدار وزن عمود الهواء القائم فوق مساحة 1 متر مربع فوق سطح البحر، مقسومًا على تلك المساحة. ووحدة البار (bar) وهي الضغط الناتج من تأثير قوة قدرها 100 ألف نيوتن على مساحة قدرها 1 متر مربع. والوحدة الأخيرة هي رطل لكل بوصة مربعة (pound per square inch ويرمز لها بالرمز psi). والمعادلات التالية توضح العلاقة الرياضية بين الوحدات المختلفة:
1atm = 101325 pa
1bar = 100000 pa
1psi = 6894.73 pa
الضغط عند نقطة
الضغط كمية قياسية، ليست متجهة، والضغط عند أي نقطة له نفس القيمة في كل الاتجاهات. هكذا تنسكب الحقائق على رؤوسنا قطعة واحدة، لكن ما أدرانا أن هذا هو الحال، أو بطريقة أخرى، كيف يمكننا إثبات هذه الحقيقة؟
خذوا نظرة على الشكل التالي ودعونا نتفق على بعض النقاط. المثلث الذي ترونه هذا في الحقيقة هو قطع عمودي في منشور ثلاثي، مساحة وجهه الأيسر تساوي Δz×Δy عليها ضغط P1، ومساحة سطحه السفلي تساوي Δx×Δy يؤثر عليها ضغط P2، ومساحة الوجه المائل تساوي L×Δy عليها ضغط P3. ومن تعريفنا للضغط عرفنا أنه هو ناتج قسمة القوة المؤثرة على سطحٍ ما على مساحة هذا السطح؛ إذًا القوة المؤثرة على أي من الأوجه الثلاثة تساوي حاصل ضرب الضغط في مساحة الوجه. والنظام الذي ندرسه وهو على شكل منشور، هو نظام يحتوي على مائع في حالة السكون، أي أن محصلة القوى المؤثرة عليه لا بد أن تساوي الصفر. ومن معادلة محصلة القوى في اتجاه المحور x نحصل على:
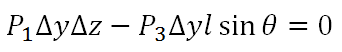
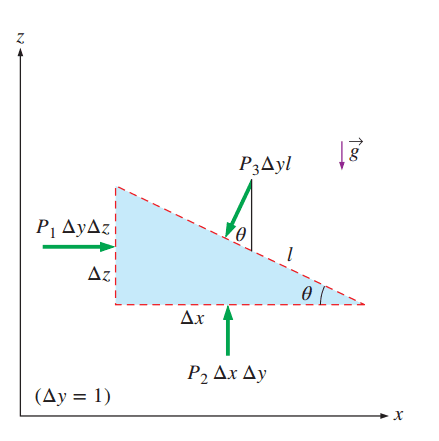
والمتمعن في الرسم يجد أن l Sinθ تساوي Δz. إذا استخدمنا هذه المعلومة لتبسيط المسألة نجد أن:
![]()
ومنها أن P1=P2.
ومن معادلة محصلة القوى في اتجاه المحور y نحصل على:
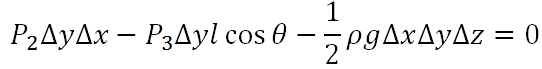
حيث إن ρgΔxΔyΔz½ هو وزن المائع داخل النظام، وρ هي كثافة المائع. وبتبسيط المعادلة حيث إن L cosθ تساوي Δx، نجد:
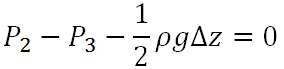
ولأننا نتحدث عن الضغط عند نقطة تجد أن Δz صغيرة جدًا تكاد تكون صفرية، لذا يمكن إهمالها وتبسيط المعادلة إلى:
P2=P3
إذًا الضغط عند أي نقطة له قسمة ثابتة في كل الاتجاهات، أو بمعنى آخر: الضغط كمية قياسية.
تغير الضغط مع تغير العمق
ضغط المائع يزداد بازدياد العمق؛ لأن الطبقات الأعمق من المائع يوجد فوقها كمية أكبر من المائع تضغط عليها، وإذا قلنا أن الضغط عند سطح مائعٍ معينٍ يساوي قيمة ثابتة P0 فإن الضغط عند أي نقطة داخل المائع تساوي:
![]()
حيث إن h هي البعد العمودي بين سطح المائع والنقطة (العمق)، وρ هي الكثافة.
وكذلك إذا كنا نريد أن نعرف الضغط عند نقطة في قعر إناء، وهذا الإناء به مجموعة من السوائل غير قابلة للامتزاج (Immiscible) فإن الضغط في أسفل الإناء يساوي:
![]()
وهذه معادلة عامة لأي عدد n من طبقات المائع. وهذه المعادلات يمكن أن نحصل منها على بعض الاستنتاجات:
- بالنسبة للغازات في نظام مغلق، إذا كانت أبعاد النظام صغيرة، يمكن اعتبار الضغط ثابت في النظام؛ لأن الفرق في الضغط بين السطح العلوي والسفلي للنظام ضئيل، فإذا افترضنا أن سقف غرفتك ارتفاعه 5 أمتار (وهو ارتفاع مبالغ فيه)، وأن ضغط الهواء عند سقف غرفتك هو 1atm فإن ضغط الهواء عند أرض غرفتك سيكون 1.006atm
- قيمة عجلة الجاذبية ثابتة تقريبًا في الارتفاعات القريبة من مستوى سطح البحر، وتساوي 9.807 متر لكل ثانية مربعة عند مستوى سطح البحر، لكن إذا كان النظام المنوط بالدراسة كبير للغاية فعلينا أن نعلم أن قيمة عجلة الجاذبية تقل كلما ارتفعنا عن مستوى سطح البحر.
- إذا كانت كثافة المائع تتغير بتغير الارتفاع (يمكننا التعبير عن ذلك رياضيًا بالقول أن (ρ=ρ(h أي أن الكثافة دالة في الارتفاع) عندها يمكننا معرفة ضغط المائع عند أي نقطة عن طريق حل معادلة تفاضلية بسيطة وهي:
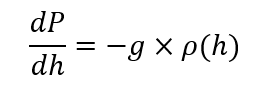
- السوائل بشكلٍ عام تعتبر غير قابلة للانضغاط، أي أن كثافتها ثابتة مهما زاد الضغط عليها. وهذا الكلام لا بأس به في حالة أن لنظامنا عمق بسيط، أما إن كانت قياساتك ستجريها في أعماق المحيط، فعليك أن تعيد النظر في الأمر.
- وأخيرًا أن ضغط المائع في أي نقطة لا يعتمد على شكل الوعاء أو حجمه، وإنما يعتمد فقط على عمق تلك النقطة فحسب.
قانون باسكال
إذا كان ضغط المائع يعتمد فقط على العمق تحت سطح المائع فإن هذا يعني أن كل النقط التي تقع في نفس المستوى الأفقي داخل مائعٍ ما، للسائل عندها نفس الضغط. فإذا وضعنا أنبوب على شكل الحرف الإنجليزي U وكانت مساحة أحد طرفيه أكبر من مساحة الطرف الآخر، وأغلقنا الأنبوب بإحكام، تكون قد تكونت لدينا رافعة. فإذا وضعت الوزن المراد رفعه أعلى السدادة الموجودة في الطرف ذي المساحة الكبرى (انظر الشكل المقابل للتوضيح) وقمنا بالضغط على الطرف الآخر بوزن أخف، فإننا سوف نتمكن من رفع الثقل؛ ذلك لأن الضغط في الطرفين متساوٍ لأنهما على نفس الارتفاع، والضغط يساوي ناتج قسمة القوة على المساحة. يمكننا كتابة هذا الكلام على الصورة:
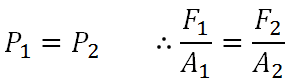
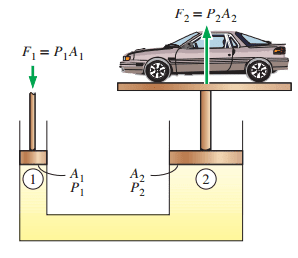
حيث إن F2 هي القوة المؤثرة على الوزن المراد رفعه وهي من المعادلة تساوي:
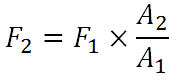
ومن المعادلة نلاحظ أن المعامل المضروب في F1 هو معامل أكبر من الواحد، ويسمى بالفائدة الميكانيكية المثالية (Ideal Mechanical Advantage). وقانون باسكال يمكن استخدامه لرفع أجسام ثقيلة بواسطة قوى بسيطة، نتيجة استعمال قانون باسكال كما هو مبين بالرسم التوضيحي السابق.
أجهزة قياس الضغط
البارومتر
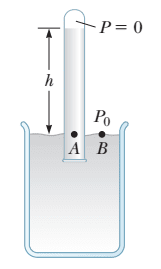
البارومتر هو جهاز يستخدم بشكلٍ أساسي لقياس الضغط الجوي، وقد صممه العالم الإيطالي إيفانجليستا توريشيلي (Evangelista Torricelli) لهذا الغرض خصيصًا، والجهاز فكرته موضحة في الصورة الآتية. إذا قمنا بإحضار حوض مليئ بالزئبق، وجئنا بأنبوب مملوء تمامًا بالزئبق طوله متر مفتوحٍ من أحد جانبيه، وقلبناه بحيث يغطس الجانب المفتوح إلى الحوض سريعًا دون أن يدخل الهواء إلى الأنبوب، سنجد أن بعض الزئبق نزل إلى الحوض، وصار ارتفاع الزئبق في الأنبوب 76 سم. الضغط عند مستوى سطح الزئبق في الأنبوب مساوٍ لقيمة الضغط الجوي، بينما الضغط عند أعلى نقطة في الأنبوب يساوي الصفر تقريبًا، وبالتعويض بكثافة الزئبق، ومقدار عجلة الجاذبية، والارتفاع -وهو 76 سم- نجد المعادلة أصبحت على الصورة:
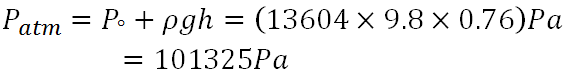
أطول شفاطة ممكنة!
دعني أقدم لك الفكرة على شكل منافسة، أتحداك أن تضع زجاجة عصير تحت شرفتك عند مستوى سطح الأرض، وأن تمد شفاطة أو خرطوم رفيع من الزجاجة إلى شرفتك، شرط أن تكون شرفتك ترتفع عن الأرض 11 مترًا أو أعلى. إن استطعت شفط العصير من الزجاجة إلى فمك باستخدام الخرطوم، سأكون في ستوكهولم العام المقبل، أصفق لك عند استلامك جائزة نوبل، لإثباتك إمكانية وجود ضغط سالب!
هذا التحدي مبني على نفس مبدأ عمل البارومتر، فإن افترضنا أنك حين تشفط السائل استطعت أن تجعل ضغط الهواء في فمك مساويًا للصفر (وهو أمر نظري بحت، فمهما حاولت ستجد ضغط الهواء في فمك مقارب ل30% من قيمة الضغط الجوي)، حينها سيرتفع السائل في الخرطوم حتى يعوض فرق الضغط داخل فمك وبين الضغط الجوي. بافتراض أنك أقوى رجل في العالم في شفط العصير، وأن ضغط الهواء في فمك مساويًا للصفر، فإن أقصى ارتفاع يمكن للماء أن يصل إليه باستخدام المعادلة السابقة هو 10 مترات، و35 سم، و8 مللمترات، وذلك إذا افترضنا أن كثافة العصير مساوية لكثافة الماء.
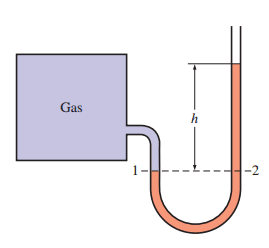
المانومتر
المانومتر هو جهاز مكون من أنبوب على شكل الحرف U مملوء بسائل، مثل الزئبق، أو الماء، أو الكحول، أو الزيوت. استخدامه الأساسي يكمن في قياس فروق الضغوط البسيطة. إذا قمنا بتوصيل أحد طرفي الأنبوب بخزان غاز، والطرف الآخر مكشوف، سنلاحظ اختلافًا في ارتفاع السائل في العمودين، وقد علمنا أن الضغط ثابت عند أي مستوى أفقي في النظام، لذا فإن الضغط عند النقطة 1 (وهو ضغط الغاز كما هو مبين في الصورة التالية) مساويًا للضغط الجوي مجموعٌ عليه ρgh، حيث h هي فرق ارتفاع السائل في العمودين.