
هنالك العديد من الإثباتات أن 0.9999 لا تساوي 1 إذًا لماذا يتكرر ظهور هذه المعادلة كحقيقة (….0.9999 = 1) ؟
لن يجادلك أحد إذا أخبرته أن (…0.3333) = (1/3) ( ولكنه سيقول لك أن (1/3) هو كسر وهذا بديهي. ربما ستشعر بوجود شيء ما خاطئ للوهلة الأولى من حدسك الرياضي المعتاد، عندما ترى الرقم الأنيق والفريد من نوعه الواحد (1)يمكن أن يُستبدل ويكون مساويًا لهذه الخانات العشرية الكثيرة والمزعجة (0.9999…). حقيقةً، الكثير منّا طالما شعر بعدم ارتياح أو تقبُّل لهذه المتساوية. ولكن الرياضيات لا تسير على حسب الأهواء.
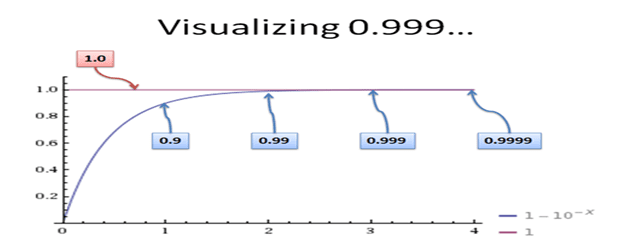
فعندما نقول ( 0.99999… ) .فإن ذلك لا يعني (0.9 ) أو( 0.99 ) أو (0.9999 ) متبوعة بعدد محدود أو نهائي من التسعات، بمعنى آخر عندما نقول:
(0.99999….) فإن ذلك يعني عدد لانهائي من التسعات. سوف يكون هناك دائما رقم 9 إضافي كل مرة بعد كل خانة عشرية. لذلك لا يوجد وجه للاعتراض أن ( 0.9999…=1 ) على أساس أنه مهما ذهبت بعيدا سيظل هذا الرقم غير مساوي للواحد، لأنه لا يوجد ما يُسمى بالنهاية أو الحد مهما ابتعدت لأنه لا نهائي ومن الممكن أن تستمر في الابتعاد وتضيف تسعة كل مرة.
ولكن سيقول البعض سيظل هنالك فرقًا بين الواحد (1) و ( 0.9999… ).حسنًا نوعًا ما نعم. عند أي توقف للعد فقط سيكون ذلك صحيحًا عند أي مرحلة من عملية التمدد عند أي رقم محدود ونهائي من التسعات سيكون هنالك فرق بين الواحد (1) و( 0.9999…..) ذلك لأنك إذا قمت بالطرح فلن يساوي الناتج صفر. ولكن النقاط المضافة تكرارًا (……) لا تنتهي وهناك دائمًا رقمًا آخر، إذًا فالمشكلة كلها تنحصر في عدم إدراك مفهوم اللانهائية.
أول شيء يجب أن ندركه حول نظام الترقيم الذي نستخدمه (الترقيم العشري) هو أن الأرقام مثل الرقم 357.9 حقيقية، أي:
«(3*100) +( 5*10) +( 7*1) + (9/10)». فحيثما تكتب رقمًا بالترقيم العشري الذي له أكثر من خانة من الأرقام فإنك تفترض ضمنيًا عملية للجمع بين أكثر من رقم.
ولذلك في الرياضيات الحديثة فإن مجموع الرموز ( 0.9999 =1) تُفهم لتُعطي معنى المجموع اللانهائي:
( 9/10 +9/100 +9/1000 +9/10000 +….. 0.9999…. = ) وهذه النقاط الكثيرة هي بدورها اختزال لـ(الحد من تسلسل الأرقام).
هنالك العديد من الطرق الرياضية التي يمكننا الاستعانة بها لإثبات أن (….0.9999 = 1). وإليك بعضًا منها:
-
الإثبات باستخدام المتواليات اللانهائية:

إذًا
(….0.9999 = 1)
.
- الإثبات عن طريق المتوالية الهندسية :
الرقم (0.9999…) يمكننا تمثيله كالآتي :
(0.9999…) = (0.9) + (0.09 ) +( 0.009 ) + ( 0.0009 ) + …
أو بمعنى آخر كل حد من حدود الجمع الغير منتهية سيكون فيه الرقم تسعة مسبوقًا بعددٍ من الأصفار قبل العلامة العشرية ويمكننا كتابته:

إذًا فالصيغة تُثبت أن (….0.9999 = 1). لاحظ أن الإثبات أعلاه يتطلب معرفة مسبقة بمسلمات وبديهيات الرياضيات إذا درست أساسيات الفلسفة الرياضية ستساعدك في استيعاب البنية النظرية المطلوبة للإثبات الرياضي.
-
الإثبات باستخدام العمليات الحسابية الأساسية (عملية الطرح):
عندما تطرح رقما من نفسه فالنتيجة ستكون صفر(0). مثال ( 4 – 4 =0 ). ولذلك ما هي النتيجة من عملية طرح (0.9999.. ) من (1) ؟


- الإثبات عن طريق إجراء القسمة المطولة:
(0.3333.. ) = ( 1/3)
من القسمة المطولة كالآتي :


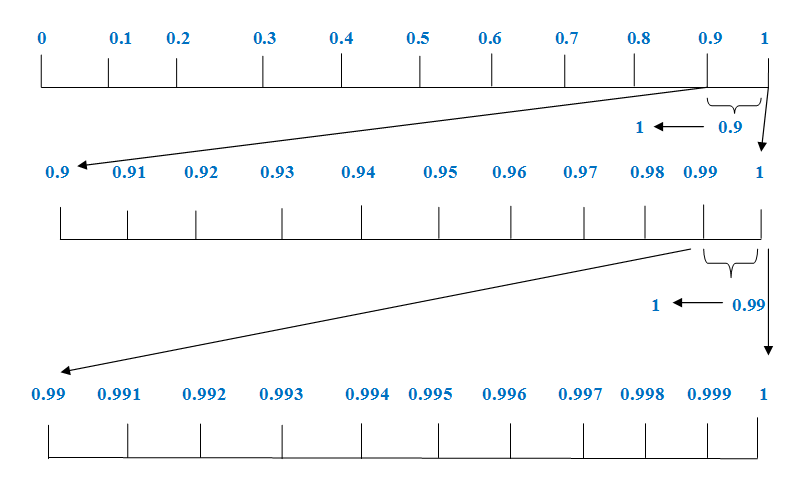
- ومنطقيا إذا كان هناك عددان مختلفان إذًا يمكنك أن تضع رقمًا آخر بينهما مثل متوسط القيمة بينهما أي في منتصف المسافة بينهما على خط الأعداد، إذًا هل تستطيع وضع رقم ينتصف الواحد و 0.9999… على خط الأعداد؟
يمكننا إيضاح ذلك عن طريق المثال الآتي: ما هي الأرقام الحقيقية التي تقع بين الرقمين أو في الفترة المغلقة من 0 إلى 1؟
أو بمعنى آخر أننا نريد إيجاد جميع الأرقام x والتي تمثل العلاقة التالية:
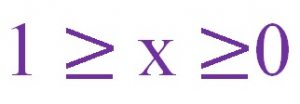

إعداد : Ahmed Hosiny
مراجعة لغوية: Mohamed Sayed Elgohary
تصميم: Mohamed Qamar-Eddine
المصادر:
http://goo.gl/gwLJ0Y
-
Leavitt, W. G. “A Theorem on Repeating Decimals.” The American Mathematical Monthly 74, no. 6 (June 1, 1967): 669–73. doi:10.2307/2314251.
-
Richman, Fred. “Is 0.999 … = 1?” Mathematics Magazine 72, no. 5 (December 1, 1999): 396–400. doi:10.2307/2690798.
-
“Sci.math FAQ: Why Is 0.9999… = 1?,” September 29, 2007. http://web.archive.org/web/20070929122649/http://www.faqs.org/faqs/sci-math-faq/specialnumbers/0.999eq1/.
-
9.999… Reasons That .999… = 1. Accessed September 18, 2015. https://www.khanacademy.org/math/recreational-math/vi-hart/infinity/v/9-999-reasons-that-999-1.


