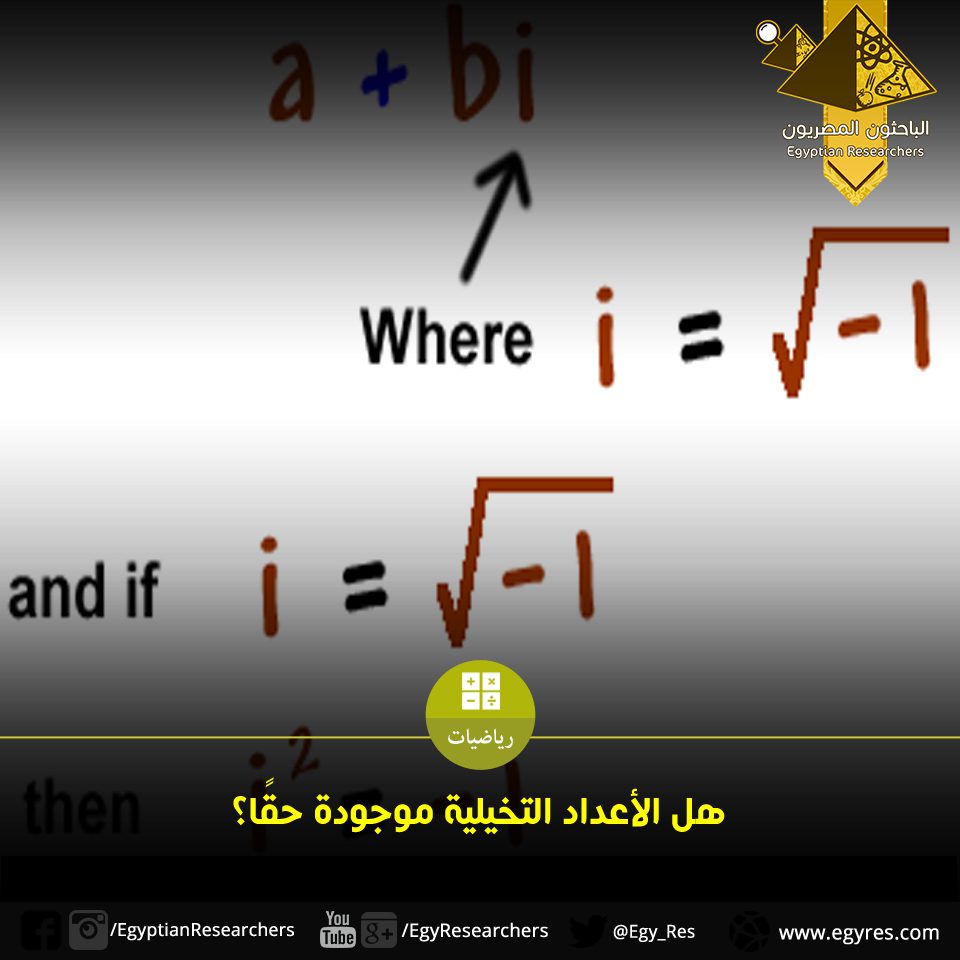
هل الأعداد التخيلية موجودةٌ حقًا؟
تتضمن الأعداد التخيلية عمليةَ إيجاد الجذر التربيعي للواحدِ السالب. ومعظم غير الرياضيين يجدون صعوبةً في تَقبُّلِ أنَّ مثل هذا الرقم ذو فائدةٍ ومعنى. وعلى العكس من ذلك، هم يلمسون أن الأرقام الحقيقية لها معاني واضحة ومفيدة. إذن، ما هي أفضل طريقة نُبيِّن بها لغير الرياضيين مدى أهمية ومعنى الأعداد المُركَّبة بنفس الطريقة التي يُمكننا بها إظهار أهمية الأعداد الحقيقية لهم؟ هذا ليس سؤالًا أفلاطونيًّا عن حقيقةِ الرياضيات، وهل هي مُجرَّدة أم هي كياناتٌ فيزيائية ملموسة قائمة بذاتها. ولكن محاولةً لبناءِ جسرٍ من التواصل والتفاهم وملء الفجوة التي يخوضها كثيرٌ من الناس عند التعرض للأعداد التخيلية للوهلة الأولى.
في الحقيقة إن تطبيقات الأعداد المُركبة لا نهائية، وتمسُّ جوانب كثيرة من حياتنا وواقعنا وساهمت بشكلٍ لا يمكنك تصوره في تقدُّم العلومِ المختلفة. فلا يكاد أن يخلو علمٌ من وجودها، بل إن بعض العلوم قامت كليًّا على وجود الأعداد العقدية مثل علم الكم quantum .
ستجد الأعداد المُركَّبة في ميكانيكا الموائع وعلم الفوضى والكسيريات والكهربية والمغناطيسية والاهتزازات الميكانيكية وغيرها، وسنحاول معًا فهم ماهية هذه الأعداد.
أين يمكننا أن نجد الأرقام العقدية بجزئها التخيلي في الحياة الواقعية؟
إن أسس ومفاهيم الرياضيات قد لا تكون ملموسةً خارجَ العلم نفسه، أي أنه يوجد بعض الثوابت والمفاهيم التي وُجِدَت فقط لتُسهِّلَ العمل نفسه.
فيمكننا أن نُقسِّم الإجابة عن هذا السؤال إلى جزئين مُنفصلين:
- كميات من واقع الحياة، والتي تُوصف بصورةٍ طبيعية بواسطة الأعداد العقدية فقط. أي أنَّ مجموعة الأعداد الحقيقية أو أي مجموعة جزئية من النظم العددية سيعتريها قصورٌ في توصيف هذه الظواهر. أي أنها ظواهر تعتمد كليًّا في توصيفها على استخدام الأعداد العقدية.
- ظواهر من واقع الحياة، والتي على الرغم من إمكانية توصيفها بالأرقام الحقيقية فإنه لا يكتمل فهمها إلَّا بإقحامِ مفاهيم الأعداد التخيلية.
المشكلة هي أن غالبية الناس يبحثون عن أمثلة للنوع الأول من التطبيقات التي بدورها نادرة فعليًّا، بينما الأمثلة من النوع الثاني تجدها بوفرة في التطبيقات المختلفة للعلوم. وإليك أكثر الأمثلةِ شيوعًا من النوع الأول:
# في مجال «الهندسة الكهربية electrical engineering»:
حالة عنصر من الدائرة الإلكترونية يُوصف عن طريق عددين حقيقيين (الجهد والتيار المتدفق من خلالهاV&I) وعنصر الدائرة الإلكترونية أيضًا يمكنه أن يُولِّد الحث والسعة (capacitance& inductance C & L ) والتي بدورها تُعتبر تمثيلًا على ميلها لمعاوقة التغيرات في الجهد والتيار تباعًا.
وهذه الكميات لن تجد أفضلَ من الأعدادِ المركبة لتوصفها توصيفًا دقيقًا. بدلًا من وجوب توصيف عنصرٍ من الدائرة عن طريق تمثيله برقمين حقيقيين V&I فإنه يمكنك توصيفه برقمِ مُركَّبٍ واحد Z= V +iL . وبالمثل، فإن الحث والسعة يمكن توصيفها برقم مركبٍ واحدٍ أيضًا W = C + il . وقوانين الكهربية يمكن التعبير عنها مستخدمين الجمع والضرب المركبين. مثالٌ آخر على النوع الأول:
# في «المغناطيسية electromagnetism»:
بدلًا من محاولة توصيف المجال الكهرومغناطيسي عن طريق كميتين حقيقيتين
قوة المجال الكهربي electric field strength وقوة المجال المغناطيسي magnetic field strength، يمكننا توصيفه بطريقةٍ أفضل مستخدمين عددًا مُركَّبًا واحدًا والذي تكون فيه المكونات الكهربية والمغناطيسية هم ببساطة الجزئين الحقيقي والتخيلي للعدد المركب. الشيء الذي ينقصنا الآن يكمن في السؤالِ التالي: لماذا تحديدًا الأعداد العقدية بجزئيها الحقيقي والتخيلي بديلًا عن متجهين ثنائيي البعد مناسبين من الأعداد الحقيقية لتوصيف هذه الظواهر؟
أو بمعنًى آخر، ما هي الخصائص الفيزيائية لعملية الضرب المُركَّبة؟ لست متأكدًا من إمكانية إجابة هذا السؤال دون الخوض عميقًا في الفيزياء. ولكن يمكننا أن نأخذ حزمةً ضوئية تمرُّ خلال وسطٍ معين، والذي بدوره يُقلِّل من كثافة الحزمة (يعاوقها) وتحدث إزاحة في زاوية سقوط الحزمة الضوئية على هذا الوسط (وليكن وسطًا زجاجيًّا مثلًا أو وسطًا مائعًا). وكيف أن هذا يُمثِّل عملية الضرب لعددٍ مركب وحيد في أبسط صوره.
أما بالنسبة للنوع الثاني فإنه الأكثر أهمية في التطبيقات فى الأعداد المركبة. وهذا النوع هو الأكثر صعوبة في الفهم بالنسبة للأشخاص غير المتخصصين، وهذا ما سنحاول تبسيطهُ الآن. وسنقوم بتوضيح ذلك عن طريق مفهوم الـanalogy أو التشابه الوظيفي للأنظمة المختلفة.
حسنًا الآن فكر معي في نوعين من التجمعات البشرية populations، التجمع الأول 236 حيث إن 48 منهم من الأطفال، والتجمع الثاني 1234 و123 منهم من الأطفال. ربما تقول أن نسبة الأطفال في التجمع الأول 48/236 تقريبًا=0.2 أقلُّ بكثيرٍ من 123/1234 والذي يُساوي 0.1، ولذلك فإن التجمع الأول أصغر التجمعين سنًّا. الآن يظهر أنك استخدمت الكسور في عملية التقييم وهي أعداد غير صحيحة non –integer numbers في مسألة ليس لها صلة بالفيزياء من قريبٍ أو بعيد. لا تستطيع قياس التجمعات البشرية عن طريق الكسور، فعلى سبيل المثال لا يوجد نصف شخص مثلًا فيزيائيًّا! إن مجموعة الأرقام التي لها صلةٌ مباشرة بقياس تعداد البشر في تجمعٍ معين هي الأرقام الطبيعية والصحيحة، والكسور ما هي إلا كائنات فضائية بالنسبة لقياس هذه الكمية الواقعية. وكذلك تبدو الأعداد المركبة عند استخدامها في قياس معظم القياسات في الحياة الواقعية. ومع ذلك فإننا بسماحنا لأنفسنا أن ننتقل من استخدام الأعداد الطبيعية إلى مجموعةٍ أكبر من الأعداد وهي rational numbers مكننا من استنتاج شيءٍ ما بصورةٍ أفضل وأدق عن موقف حقيقي في الحياة. حتى وإن كانت القياسات في هذا التطبيق الواقعي لا تنطبق إلا على الأعداد الطبيعية. بالطريقة ذاتها كوننا أردنا أن نفكر ماذا سيحدث إذا استخدمنا المجموعة الأكبر من الأعداد متضمنة الأعداد المركبة وماذا سنتمكن من اكتشافه حيال أمرٍ ما وماذا ستكون النتائج في التطبيقات من العالم الواقعي حتى وإن كانت القياسات الحقيقية لهذه التطبيقات تتضمن فقط استخدام الأرقام الحقيقية فقط. هذا يحدث بالفعل طوال الوقت في التطبيقات الهندسية.
إعداد :Ahmed Hosiny
مراجعة علمية: Eslam Samy
مراجعة لغوية: Mohamed Sayed Elgohary
تحرير: ندى المليجي
المصادر:
#الباحثون_المصريون.

