قُدمَت هذه المعادلات ذات المظهر البسيط، ولكن فيما بعد كان لها عواقب وتطبيقات كبيرة في العلوم والمجتمع والتكنولوجيا. دعونا نُلقي نظرة على الصيغ العشر الأكثر تأثيرًا في الفيزياء (بدون ترتيب معين) والتي غيّرت مجرى التاريخ.
قانون الحركة الثاني
القوة، التي غالبًا ما تُوصَف بشكل بديهيّ بأنها دفع أو سحب، هي في الحقيقة مصدرُ التسارع في جُسيم متحرك. بدون أن يأتي من أي وكالة خارجية، لا يمكن للجُسيم أن يخضع للتغيير في الطريقة التي يسير بها. حدد نيوتن القوة رسميًا في عام 1686 في المعادلة الشهيرة F = ma.
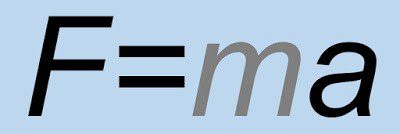
يُخبرك بمدى قوة المحرك لسحب السيارة، ومقدار الدفع المطلوب لرفع صاروخ، وإلى أي مدى تطير كرة المدفع وما إلى ذلك. ولكن الأهم من ذلك، ساعدت المعادلة في فضح المعتقدات الأرسطية التي ظلّت دون منازع لآلاف السنين.
وفقًا لأرسطو، القوة ضرورية للحفاظ على حركة الجسم. لماذا ستتوقف الكرة المتدحرجة على الأرض في النهاية؟ لأنه -كما قال أرسطو- لم تُعد تُدفع، ولهذا السبب بعد ذلك، أوضح العالم الإيطالي جاليليو جاليلي في القرن السابع عشر من خلال التجربة:
«توقفت الكرة لأن الأرض كانت قوية وكانت ناعمة بما فيه الكفاية، ستدحرج الكرة إلى الأبد. لا قوة مطلوبة!»

قال نيوتن كذلك:
«إن حالة السكون أو الحركة الخطية المنتظمة تعنيان تسارعًا صفريًا. وبالتالي سيبقى الجُسيم في مكانه أو يستمر في التحرك بنفس المعدل وسيحافظ على نفسه في الحالة التي كان عليها حتى بالطبع عندما يتم التعامل معه بقوة خارجية.»
العلاقة بين الطاقة والكتلة
ينبع من النظرية النسبيّة الخاصة أنّ الكتلة والطاقة كليهما مظاهر مختلفة لنفس الشيء. كتلة الجسم هي مقياس لمحتوى طاقته. فإذا تم تحويل 1 جرام من الكتلة إلى طاقة، فسيكون 90 تريليون چول. هذا يعادل الطاقة المنبعثة من لمبة 100 واط لمدة 30000 سنة!

ومن المهم معرفة أن أشهر معادلة لأينشتاين ليست عمله الرئيسي. الصيغة معروفة جدًا بسبب ارتباطها بالقنبلة الذرية. وقال أينشتاين نفسه:
«لو توقعت هيروشيما وناغازاكي، لكنت مزقت صيغتي في عام 1905.»
على الرغم من أنه لعب دورًا ثانويًا في مشروع مانهاتن.
مبدأ عدم اليقين
صاغه فيرنر هايزنبرغ (Werner Heisenberg)عام 1927، مبدأ عدم اليقين وهو أحد الأركان الأساسية لميكانيكا الكم. وأنهت المعادلة بمفردها الحتمية الكلاسيكية؛ بمعنى أنه في عالم الذرات المُتناهية الصغر فإن الصدفة لها دورها ودراما الوجود ليست محددة سلفًا بشكل مطلق.

في أكثر أشكال المعادلة شيوعًا، تقول أنه كلما كان قياس الموضع أكثرَ دقة كان قياس الزخم غيرَ دقيق، والعكس صحيح. وبالتالي، لا يمكن للمرء أن يعرف بدقة تامة كلا هذين العاملين المهمين اللذين يحددان حركة أحد أصغر الجُسيمات، موقعه وسرعته، في نفس اللحظة.
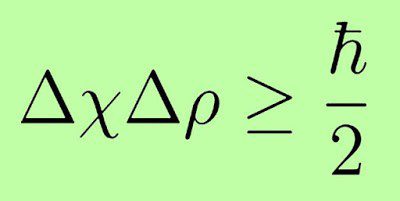
رُفضَ مبدأ عدم اليقين على الفور من قبل علماء الفيزياء البارزين في ذلك الوقت، بما في ذلك ألبرت أينشتاين. وبذل نيلز بور( Niels Bohr) قصارى جهده لإقناع أينشتاين بإن علاقة عدم اليقين هي قانون أساسيّ في الفيزياء. وما زال أينشتاين يرفض، واتفقوا على عدم الموافقة. وبحلول عام 1933، أصبح الوضع السياسيّ أسوأ بكثير في ألمانيا، وانتقل أينشتاين إلى الولايات المتحدة.
في عام 1954، زار هايزنبرغ منزل أينشتاين في برينستون. تحدثوا فقط عن الفيزياء، لكن موقف أينشتاين من المبدأ لم يتغير. في عام 1955، توفي أينشتاين تاركًا فيرنر هايزنبرغ محبطًا لأنه فشل في الحصول على تأييد أينشتاين لعلاقة عدم اليقين الخاصة به.
على الرغم من أنّ أينشتاين وآخرين اعترضوا على آراء هايزنبرج وبور، إلا أن أينشتاين كان عليه أن يعترف بأنها كانت بالفعل نتيجة منطقية لميكانيكا الكم. لكن بالنسبة لأينشتاين، كان هناك شيءٌ ما مفقود، وكانت ميكانيكا الكم غير مكتملة، فقد ادعى مجازًا:
«أنا مقتنع بأن الله لا يرمي النرد.»
حافظ هايزنبرغ، بدعم من بوهر وباولي وشرودنجر وآخرين، حتى وفاته على أنّ عدم اليقين الكمومي غيرَ دقيقٍ للقياس، بل متأصلٍ في الظواهر الكمومية. يؤدي إلى نتائج احتمالية وليست حتمية.
معادلة ماكسويل فاراداي
في عام 1831، كما تُروى القصة عادةً، تلقّى رئيس الوزراء أو بعض السياسيين البارزين عرضًا للحث الكهرومغناطيسي بواسطة فاراداي ( Faraday). عندما سُئِل: «ما فائدة ذلك؟» أجاب فاراداي: «ما فائدة المولود الجديد؟» مرت خمسون عامًا قبل أن تنطلق الطاقة الكهربائية حقًا كما تصورها فاراداي.
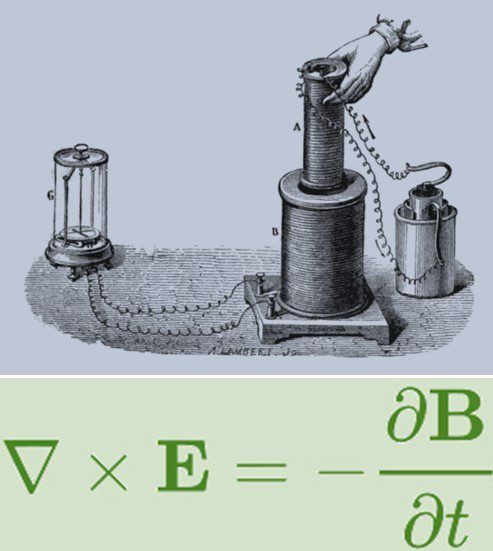
وتستفيد المولدات والمحركات من قانون فاراداي. أصبحت معادلة ماكسويل أساس توليد الطاقة وبالتالي جعل فاراداي أبًا للكهرباء. قال ماكسويل عن فاراداي:
«إنّه -ويجب أنّ يظلَّ دائمًا- والدُ ذلك العلم الموسّع للكهرومغناطيسية.»
معادلة ديراك
التماثل هو الكلمة الأساسيّة للفيزياء وقد استخدمها ديراك (Paul Adrien Maurice Dirac) بشكل مثاليّ في عام 1928. طورّ معادلة تُوضح رقم الدوران كنتيجة لاتحاد ميكانيكا الكم والنسبيّة الخاصة. تنبأت المعادلة أيضًا بوجود مادة مضادة، لم تكن مُتوقعة سابقًا وغيرَ ملحوظة، والتي تم اكتشافها تجريبيًّا في عام 1932.
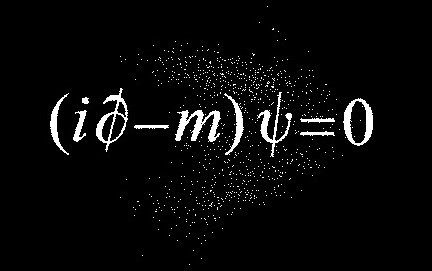
وُصِف الإنجاز على قدم المساواة مع أعمال نيوتن وماكسويل وأينشتاين قبله. حتى أن ديراك قد تكهن بإمكانية وجود مرآة من الجُسيمات المضادة، وبالتالي يُصبح مصدر إلهامٍ لكُتّاب الخيال العلميّ. اشتهر ديراك أيضًا بمساهمته في الديناميكا الكهربيّة الكموميّة، والتي وصفت كيف ستعمل القوى الكهربائية والمغناطيسية على مقياس الأشياء الأصغر من الذرات.
قانون الانتروبيا
اللامساواة الشهيرة التي تقول أنه عندما تتغير الطاقة من شكل إلى آخر، أو عندما تتحرك المادة بحرّية، يزداد الاضطراب في نظامٍ مغلق. وفقًا لعالم الفلك الشهير آرثر إدينجتون (Arthur Eddington):
«القانون الذي يزيد الانتروبيا دائمًا يحتفظ -كما أعتقد- بالمكانة الأسمى بين قوانين الطبيعة.»
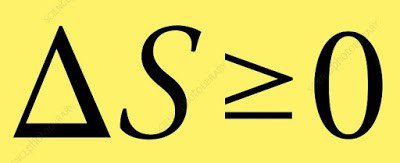
لا ينطبق مفهوم القانون الثاني للديناميكا الحرارية على محركات الاحتراق الداخلي المستخدمة في سياراتنا ودراجاتنا النارية وسُفننا وطائراتِنا فحسب، بل ينطبق أيضًا على شرح عمليات الحياة، عند النظر إليها من منظور العمليات الدورية.
للقانون الثاني أيضًا عواقبُ عميقة على الكون على نطاق واسع. تخيّل أنْ يتم عرض مقطع فيديو لكوب يتم إسقاطه وكسره. من الواضح أنك ستكون قادرًا على معرفة ما إذا كان يتم تشغيل الفيديو للخلف أو للأمام، من تدفق الكون.
وبالمثل، إذا تم عرض فيلم كوننا بشكل عكسي، فسيصبح الكون مرتبًا أكثر فأكثر، مثل الكأس، وعندما يتم تشغيله للأمام، نتوقع أن يتم تنظيمه، مثلَ قطع الكأس المكسورة.
معادلات مجال أينشتاين
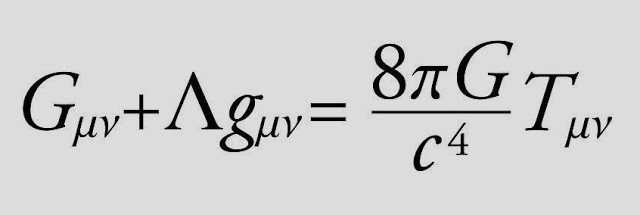
أدّت معادلات أينشتاين إلى اندماج الأبعاد الثلاثة للفضاء وبُعدٍ واحدٍ من الزمن في زمكان واحد رباعيّ الأبعاد. يُمثل التعبير الموجود على الجانب الأيسر من المعادلة انحناء الزمكان. التعبير الموجود على اليمين هو كثافة طاقة الزمكان. تُملي المعادلة كيف تحدد الطاقة انحناء المكان والزمان.
قدّم أينشتاين مصطلح الثابت الكوني (Λ) لعدم السماح للكون أن يتمدد أو يتقلص. لم ينجح هذا الجهد لأنه في عام 1929، اكتشف الفلكي إدوين هابل أدلة على توسع الكون. دعا هابل أينشتاين ليرى بنفسه أن الكون يتغير بالفعل.
نتيجةً لذلك، تخلّى أينشتاين عن الثابت الكوني في المعادلة، واصفًا إياه بأنّه أكبرَ خطأٍ فادح ارتكبه على الإطلاق. لذلك، منذ الثلاثينيات وحتى أواخر التسعينيات، افترض معظم الفيزيائيين أنّ الثابت الكونيّ يُساوي صفرًا. ولكنْ، وجدت تقنيات علم الفلك المحسّنة مؤخرًا أن تمدد الكون يتسارع مما يدل على القيمة غير الصفرية للثابت.
لماذا تعتبر معادلات مجال أينشتاين مهمة في الفيزياء؟ أولاً، لأنها توحد مفهومي المكان والزمان، اللذين اعتُبِرا سابقًا منفصلين بحدسنا، في زمكانٍ واحد. تمامًا مثل ماكسويل وحدَّد الكهرباء والمغناطيسية إلى كهرومغناطيسية في القرن التاسع عشر.
ثانيًا، يصفون التفاعل -وليس القوة- الأساسي للجاذبية نتيجة انحناء الزمكان بواسطة الطاقة (الكتلة أيضًا هي طاقة من معادلة أينشتاين للطاقة والكتلة).
على الرغم من أنّ نيوتن قد أعطى معادلة لحساب مقدار قوة الجاذبية بين أي جسمين من الكتلة تفصل بينهما مسافة، إلا أنّه لم يشرح سبب الجاذبية في المقام الأول.
معادلة الموجة
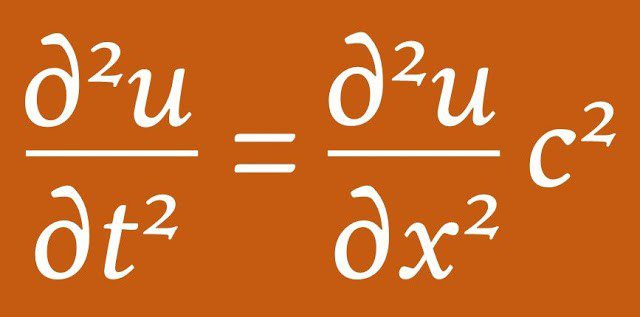
معادلة الموجة أحاديّة البعد لها دالة عددية (u) لمتغير فضائي واحد، ومتغير زمني واحد لأن الموجات تنتشر في الفضاء، وفي الوقت أيضًا. كُتبَت هذه المعادلة لأول مرة بواسطة عالم الرياضيات الفرنسي جان لو روند دالمبرت (Jean Le Rond d’Alembert)، ومن ثمْ يُطلق عليها أحيانًا أيضًا معادلة دالمبيرت. كتبه عالم الرياضيات والفيزيائي السويسري ليونارد أويلر (Leonhard Euler) في ثلاثة أبعاد عام 1707.
نحن محاطون باستمرارٍ بالأمواج، سواءً أدركناها أم لا، فهي موجودة دائمًا، كأن تعزف على الجيتارمثلًا أو تُسقِط حجرًا في بركة. ومعادلة الموجة ليست أنيقة مثل المعادلات الأخرى في هذه القائمة ولكنها رائدة حيث تم تطبيقها على الموجات الصوتية (والأدوات) والموجات في السوائل والموجات في الزلازل والموجات الضوئية وميكانيكا الكم والنسبيّة العامة.
معادلة بلانك
هذه الصيغة مسؤولة عن ولادة ميكانيكا الكم، وكذلك الخلايا الشمسية والتلفزيونيّة. افترض الفيزيائيّ الألمانيّ الرائد في ذلك الوقت ماكس بلانك (Max Planck) في عام 1900، أنّ هذه الطاقة كانت محددة كمّيًا ويمكن أن تنبعث أو تمتص فقط في مضاعفات متكاملة لوحدة صغيرة، والتي أطلق عليها اسم «كمّية الطاقة».
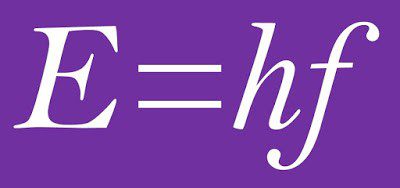
وسع أينشتاين فكرة بلانك في عام 1905 عندما قدم مفهوم «الكم الخفيف» أو جُسيم الضوء أو الفوتون. وبالتالي، لم يكن الإشعاع الكهرومغناطيسي مستمرًا مثل الموجة ولكنّه منعزلٌ في حزم الضوء، كما اقترح أينشتاين.
قدّم بلانك المعادلة ببساطة كخدعة لحل مشكلة إشعاع الجسم الأسود، لكن أينشتاين تصوره أن يكون أكثر. وفي عام 1887، عثر المجرب هاينريش هيرتز (Heinrich Hertz) على التأثير الكهروضوئي لأول مرة. وانبعاث الإلكترونات عندما يصطدم ضوء بتردد معين بمادة ما.
ظلّت ظاهرة التأثير الكهروضوئي غيرَ مُفسرةٍ إلى حد كبير، حتّى مع نظرية الموجة للضوء، حتى وصول علاقة بلانك-أينشتاين في عام 1905. وصفها أينشتاين من حيث تفاعل الجُسيمات بين الفوتون والإلكترون. قائًلًا:
«تحت بعض الترددات الحرجة، لا يوجد فوتون لديه طاقة كافية لإخراج الإلكترون.»
هذا يعني أنه إذا كانت مادة حساسة للضوء تتطلب فوتونات من الضوء الأزرق لإصدار الإلكترونات، وهي سمة من سمات المادة، فلن تتمكن فوتونات الضوء الأخضر أو الأصفر من إخراج الإلكترونات من المادة.
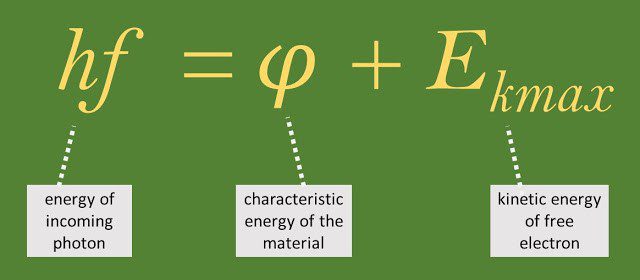
يتم امتصاص الطاقة المميزة أو دالة الشغل للمادة، لفك الروابط، ثُمّ يتم ملاحظة ما تبقى من الطاقة كطاقة حركية للإلكترون الحر. كان توضيحُ أينشتاين متسقًا مع قانون الحفاظ على الطاقة. حصل على جائزة نوبل في الفيزياء لتفسيره للتأثير الكهروضوئي (وليس لعلاقة الطاقة والكتلة أو النسبية).
قال بلانك:
«إنّ تقديمه لـ”الكم” في عام 1900 كان فعلًا يائسًا.»
لكن عندما تبناه أينشتاين وأعطاه معنىً، بدأ نقاشٌ جديدٌ بالكامل وألغيت القوانين القديمة في غضون عقد أو نحو ذلك. ورفض أينشتاين -الذي كان مسؤولاً عن ذلك- تأييد الثورة الكمومية الجديدة.
وأصبح اكتشاف بلانك وأينشتاين أساسًا لجميع فيزياء القرن العشرين، والتي بدونها، لم يكن من الممكن إنشاء نظرية عملية للجزيئات والذرات وعمليات الطاقة التي تحكم تحولاتها.
معادلة شرودنجر
في أطروحة الدكتوراة عام 1924، اقترح الفيزيائيّ الفرنسيّ لويس دي برولي (Louis de Broglie)، أنه مثلما يمتلك الضوء خصائص الموجة والجُسيمات، يجب أن تكون لدى الإلكترونات أيضًا خصائص تشبه الموجة؛ من أجل دعم تناظر مادة الطاقة. وبعد ذلك بعامين، في عام 1926، نشر العالم النمساوي إروين شرودنغر (Erwin Schrödinger) معادلة تصف كيف يجب أن تتطور موجة المادة في المكان والزمان.
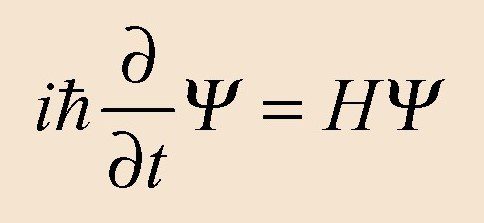
وتمامًا مثل معادلات نيوتن التي تُستخدم لحساب سلوك كرة القدم عند ركلها، يمكنك استخدام معادلة شرودنجر لحساب سلوك الإلكترون في مدار الذرة. بشكلٍ عام، تُستخدَم في العديد من العمليات الحسابية في ميكانيكا الكم وهي أيضًا أساس لكثير من التكنولوجيا الحديثة، من الليزر إلى الترانزستورات، والتطوير المستقبلي لأجهزة الكمبيوتر الكمومية.


2 Responses
من الجميل سماع مثل هذه المعلومات احسنتم صنعاً أمين يوسف وMostafa A tallah و حسام إبراهيم و داليا شافعي السيد ??