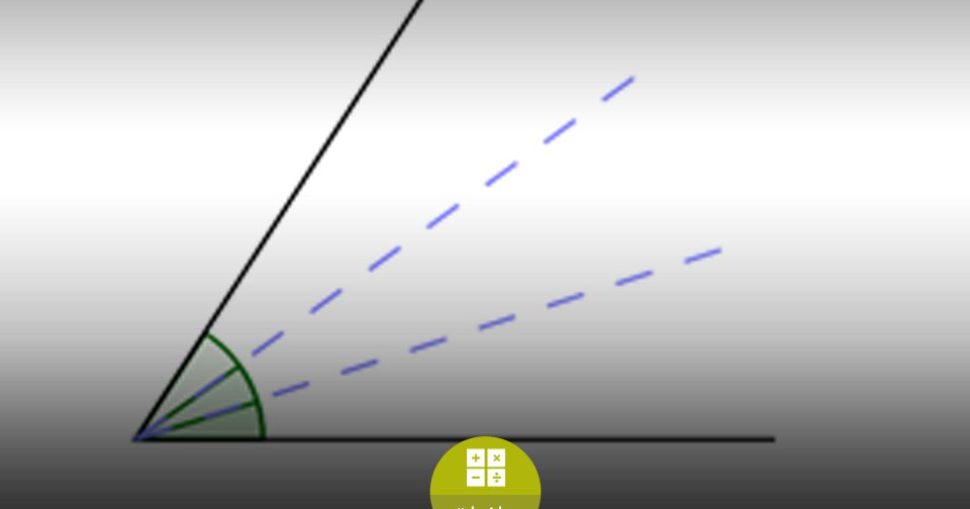
تثليث الزاوية :
يعتبر تثليث الزاويا من أشهر المسائل في تاريخ الرياضيات، أي تقسيمها إلى ثلاثة أقسام متساوية باستخدام فرجار ومسطرة غير مدرجة (أو ما يدعى بالإنشاء الهندسي). يمكننا، بالطبع، قياس أي زاوية معطاة باستخدام منقلة، ثم تقسيم النتيجة على 3 ورسم الخطوط اللازمة بعد ذلك، لكن بافتراض أن المنقلة ممنوعة، تتكون المشكلة التي تعود إلى أيام الإغريق القدماء، الذين بنوا العديد من إنشاءاتهم مستخدمين هاتين الأداتين فقط (الفرجار والمسطرة غير المدرجة).
حتى تسنطيع التعرف على كيفية حل هذا النوع من المشاكل، لنبدأ بتقسيم زاوية معينة إلى قسمين متساويين، بدلاً من ثلاثة ..
تنصيف زاوية :
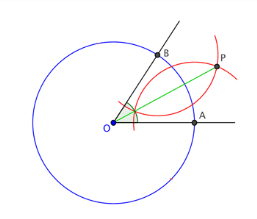
لتكن لدينا نقطة تقاطع لخطين (O)، يمكننا تنصيف الزاوية بين هذين الخطين المتقاطعين في O كما يلي:
ضع رأس الفرجار في (O) وارسم دائرة (بأي قطر ترغب به) وهي الدائرة الزرقاء في الشكل، ستتقاطع الدائرة مع الخطين في نقطتين هما (A) و (B) .. ضع الآن رأس الفرجار في (A) وارسم قوس دائرة (قطرها لا يتجاوز الطول الفاصل بين النقطتين (A) و (B) وأكبر من منتصف هذا الطول) كما هو مبين في الشكل، ثم ارسم قوساً آخر مركزه النقطة (B) محافظاً على نصف قطر الدائرة المرسومة من النقطة (A) (وهما القوسان باللون الأحمر في الشكل). لتكن نقطة تقاطع القوسين هي (P) .. سيكون المنصف للزاوية هو الخط الواصل بين (O) و (P).[1]
تثليث زاوية :
الآن .. ماذا عن تقسيم الزاوية إلى ثلاثة أقسام ؟ لماذا هو بتلك الصعوبة ؟ يوجد عدة حالات خاصة يمكننا القيام بذلك فيها، فإذا كانت الزاوية قائمة (90 درجة) على سبيل المثال[2]، يمكننا تثليث أي زاوية إذا سمحت لنفسك باستخدام بعد إضافي[3]. بإمكانك أيضاً تثليث أي زاوية إن استخدمت مسطرة مدرجة عوضاً عن المسطرة غير المدرجة[4].
بقيت مشكلة إمكانية تثليث زاوية لغزاً محيراً لآلاف السنين، حتى عام 1837 الذي أثبت فيه الرياضي بيير وانتزل استحالة ذلك، و وانتزل هو رياضي فرنسي وخبير في علم الحساب. وقد فعل ذلك ولم يتجاوز عمره 23 عاماً، لكنه توفي للأسف في سن مبكرة عن 33 عاماً.
لماذا يستحيل ذلك ؟ أظهر وانتزل أن مشكلة تثليث الزاوية هي مكافئة لحل معادلة تكعيبية باستخدام الإنشاء الهندسي. أظهر وانتزل أنه من الممكن حل بضع معادلات تكعيبية بذلك الأسلوب ولا يمكننا حل معظمها. واستنتج عبر ذلك أن معظم الزوايا لا يمكن تثليثها.
لا تستسلم
رغم أن وانتزل برهن أن زاوية عشوائية غير قابلة للتثليث باستخدام مسطرة غير مدرجة وفرجار .. لكن هذا لم يوقف الناس عن المحاولة، فما زال العديد من الهواة يراسلون الكثير من الهيئات والجامعات ببراهين مختلفة حول هذه المشكلة، لكن كما هو جلي، فإن جميعها تحوي أخطاءاً في مرحلة ما.
إعداد: Abdelraheem ghzal
مراجعة: إسلام سامي
تحرير: ندى المليجي
المصادر: https://goo.gl/Opikmk
[1] يمكنكم مراجعة البرهان من هنا :
http://www.mathopenref.com/constbisectangle.html
[2] لتوضيح ذلك راجع :
https://www.youtube.com/watch?v=sBQM42yPQL4
[3] لمتابعة الموضوع راجع :
https://plus.maths.org/content/trisecting-angle-ruler
[4] يمكنك مراجعة :